2.5. Функциональные соответствия и их виды

В курсе математического анализа были изучены различные функции на множестве действительных чисел. Эти функции можно рассматривать как бинарные отношения на множестве , где– область определения функции,– множество ее значений. Например, функцияесть бинарное отношение на множестве, функция– бинарное отношение на множестве. Из математического анализа известно, что основной признак функционального соответствия таков:каждому элементу области определения соответствует определенный единственный элемент множества значений.

Рассмотрим подход к понятию функционального соответствия как к особому виду бинарных отношений, заданных на произвольном множестве.

Определение 2.10. Функциональным соответствием на множестве называют бинарное отношение , в котором каждый элемент множестваимеет единственный образ во множестве.

Примечание 1. Матрица функционального соответствия– это матрица, где– число элементов множества,– число элементов множества,,. Поскольку по определению функционального соответствия каждый элемент множестваимеет единственный образ во множестве, в каждой строке матрицыодин и только один элемент равен единице, все же другие элементы строки – нули.

Примечание 2. Если множестваиимеют одинаковое число элементов=, то матрица функционального соответствияесть квадратная матрица порядка.

Рассмотрим ряд примеров.

Пусть .

Пример 1.

Пусть . Декартово произведениесодержит шесть пар, а, следовательно,подмножеств. Каждое подмножествоесть бинарное отношение на множестве, следовательно, на множествесуществует 64 различных бинарных отношений.

Чтобы бинарное отношение являлось функциональным соответствием, каждый элемент множества должен иметь единственный образ во множестве. Следовательно, график функционального соответствия может содержать только три пары, в которых на первом месте стоят элементы 1, 2, 3 множества .

На рисунке показаны графы всех возможных функциональных соответствий на множестве. Таких соответствий восемьf₁,f₂,…,f₈. Любое из них можно представить матрицей бинарного отношения:

,,,,

,,,.

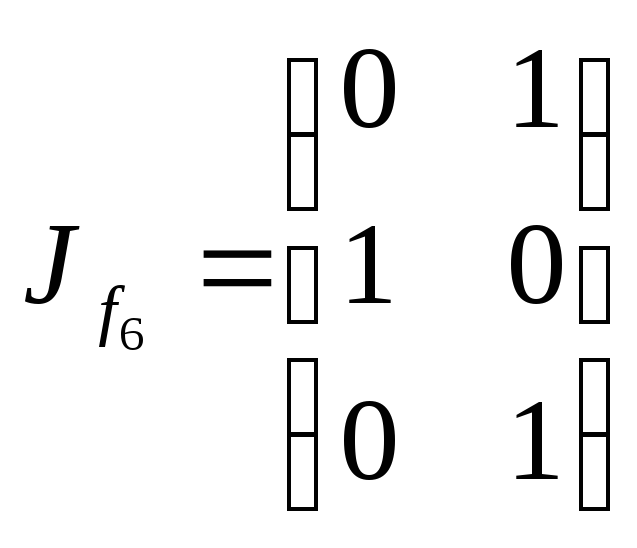Кроме представления в виде матрицы бинарного отношения, каждое функциональное соответствие можно задать также в виде двустрочной матрицы , в первой строке которой записаны элементы множества, а во второй – их образы из множества:

,,,,

,,,.

Представление функциональных соответствий в виде двустрочных матриц позволяет определить число таких соответствий. В данном случае их столько, сколько можно составить различных наборов по три элемента в каждом, используя при этом два элемента,и. Формулы для вычисления числа таких наборов рассматриваются в комбинаторике (см. главу 3).

В соответствиях f₂, f₃ , f₄ ,f₅ ,f₆ иf₇ каждый элемент множестваимеетне менее одного прообразаво множестве. Такие соответствия называютсюръективными функциональными соответствиямиилиотображениями множества на множество.

Соответствия f₁, f₈ сюръективными соответствиями не являются, поскольку один из элементов множества имеет менее одного прообраза во множестве .(Вf₁ни одного прообраза не имеет элементb, вf₈ – элементa).

Очевидно, что если существует сюръективное функциональное соответствие на множестве , то множествосодержит элементов не больше, чем множество .

Пример 2.

Пусть . Декартово произведение

содержит двенадцать пар, а, следовательно, подмножеств. Каждое подмножествоесть бинарное отношение на множестве, следовательно, на множествесуществует 4096 различных бинарных отношений.

Чтобы бинарное отношение являлось функциональным соответствием, каждый элемент множества должен иметь единственный образ во множестве. Следовательно, график функционального соответствия может содержать только три пары, в которых на первом месте стоят элементы 1, 2, 3 множества .Однако существуетспособа выбрать

образ для каждого элемента множества , т. е. на множествесуществует 64 различных функциональных соответствия.

Поскольку элементов во множестве больше, чем во множестве, ни одно из этих функциональных соответствий не является сюръективным. Рассмотрим несколько соответствий, в которых каждый элементимеетне более одного прообраза во множестве. Такие соответствия называютинъективными функциональными соответствиямиилиотображениями множества во множество .

Запишем двустрочныематрицы некоторых инъективных функциональных соответствий на множествеи построим графы этих отображений.

,,,.

Пример 3.

Пусть .

Декартово произведение содержит девять пар, а, следовательно,подмножеств. Каждое подмножествоесть бинарное отношение на множестве, следовательно, на множествесуществует 1024 различных бинарных отношения.

Чтобы бинарное отношение являлось функциональным соответствием, каждый элемент множества должен иметь единственный образ во множестве. Следовательно, график функционального соответствия может содержать только три пары, в которых на первом месте стоят элементы 1, 2, 3 множества .Однако существуетспособов выбрать образ для каждого элемента множества, т. е. на множествесуществует 27 различных функциональных соответствий.

Некоторые из этих соответствий являются одновременно сюръективными и инъективными, т.е. каждый элемент множества имеет не менее, но и не более одного прообраза во множестве. Функциональные соответствия являющиеся одновременно сюръективными и инъективными называютсявзаимно однозначными соответствиями. Возможность установить взаимно однозначное соответствие между множествами говорит о том, что в этих множествах число элементов одинаково.

Обобщим понятия, рассмотренные в примерах.

Определение 2.11. Сюръективным функциональным соответствием на множественазывают функциональное соответствие, в котором каждый элемент множества имеют не менее одного прообраза во множестве.

Сюръективное функциональное соответствие на множественазывают также отображением множества на множество .

Определение 2.12. Инъективным функциональным соответствием на множественазывают функциональное соответствие, в котором каждый элемент множества имеют не более одного прообраза во множестве.

Инъективное функциональное соответствие на множественазывают также отображением множества во множество .

Определение 2.13. Биективным функциональным соответствием на множественазывают функциональное соответствие, в котором каждый элемент множества имеют один прообраз во множестве.

Биективное функциональное соответствие на множественазывают также взаимно однозначным соответствием между множествами и .

Определение 2.14. Если между отрезком натурального ряда и множествомсуществует взаимно однозначное соответствие, то числоназываютчислом элементов множества .

Определение 2.15. Если между множеством натуральных чисел и множествомсуществует взаимно однозначное соответствие, тоназываютсчетным множеством.

Определение 2.16. Если между множеством и его правильной частью () существует взаимно однозначное соответствие, то множества и называютбесконечными множествами, если же взаимно однозначного соответствия не существует, – то конечными множествами.

Можно показать, что множества ,,являются бесконечными счетными множествами, множество- бесконечным несчетным множеством.

Если – число элементов множества , – число элементов множества, то декартово произведениесодержитэлементов и имеетподмножеств, каждое из которых является бинарным отношением. Среди нихотношений являются функциональными соответствиями. Причеместь число различных наборов изэлементов поэлементов в каждом наборе. Формулы для вычисления числа таких наборов рассматриваются в комбинаторике (см. главу 3).

Пусть – бинарное отношение на множестве, т.е..

Определение 2.17. Отношением называют отношением, противоположным отношению , если есть дополнение множествадо множества.

Определение 2.18. Отношение называют отношениемобратным отношению , если .

Рассмотрим пример.

Пример 4.

Пусть ,(см. пример 3).

На множестве зададим функциональные соответствияf₁, f₂, f₃ и f₄ матрицами бинарных отношений и двустрочными матрицами:

,,,;

,,,.

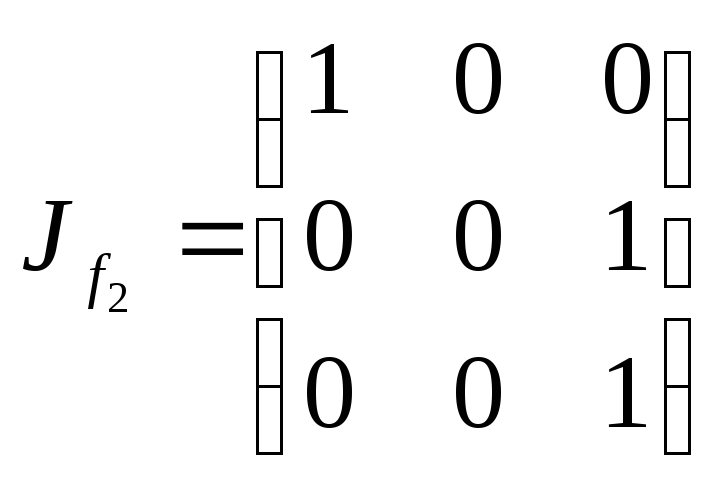Соответствия f₃ и f₄ являются взаимно однозначными соответствиями, поскольку каждый элемент множестваимеет единственный образ во множестве, и каждый элемент множестваединственный прообраз во множестве.

Запишем матрицы отношений ,,,и отношений,,,, а также,,и.

,,,;

,,,;

,,,.

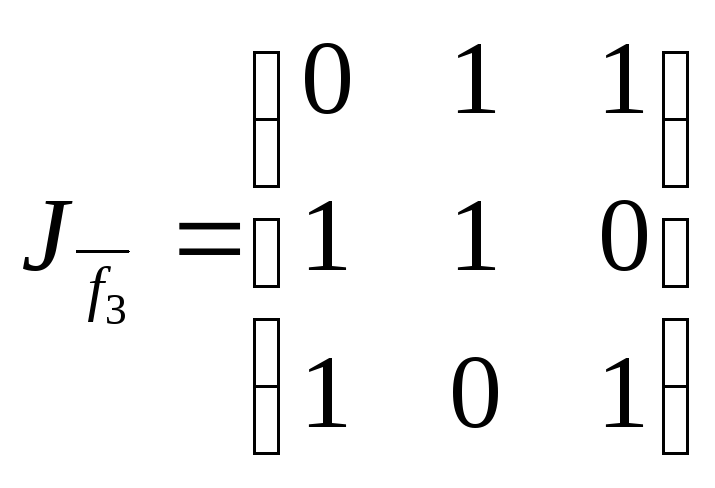Можно видеть, что только иявляются взаимно однозначными соответствиями на множестве. Представим эти соответствия двустрочными матрицами.

,.

Найдем матрицы композиций прямых и обратных отношений. Поскольку прямое отношение задано на множестве (), а обратное – на множестве , то их композицияесть отношение на множестве().

=;

=;

=;

=.

Матрицы иесть единичные матрицы, т.е. соответствияипереводят каждый элемент множествав себя. Такое отношение на множественазываюттождественным преобразованием множества .

Из примера 4 очевидны следующие утверждения.

Утверждение 1. Для того, чтобы отображение было взаимно однозначным соответствием, необходимо и достаточно, чтобы обратное ему бинарное отношениетакже являлось функциональным соответствием.

Утверждение 2. Если отображение является взаимно однозначным соответствием, то композицияесть тождественное преобразование.

Таблица 2.1 Свойства бинарных отношений
Свойство	Способы задания отношения
	График	Характеристическое свойство	Матрица отношения	Характеристическая функция
Рефлексивность		– истина,		,
Симметричность		– истина,		,
Антисимметричность		– истина,		,
Транзитивность		– истина,		,

Примечание.Символомобозначена транспонированная матрица, символом– единичная матрица.

45