2.4. Свойства и виды бинарных отношений

Наиболее важными свойствами бинарных отношений на множестве являются свойства рефлексивности, симметричности, антисимметричности и транзитивности (табл. 2.1).

Особую роль в теории бинарных отношений играют отношения эквивалентности и отношения порядка.

Определение 2.8. Отношением эквивалентности называют рефлексивное, симметричное и транзитивное отношение.

По отношению эквивалентности множество разбивается на непересекающиеся классы эквивалентности.

Определение 2.9. Классами эквивалентности множества называют подмножества множества , удовлетворяющие следующим условиям:

1) объединение всех классов есть множество ;

2) пересечение любых двух классов пусто.

Если на множестве задано отношение эквивалентности , то элементы попарно связанные друг с другом попадают в один класс, элементы из разных классов отношением не связаны. Множество классов эквивалентности обозначают /и называютфактор-множеством множества по отношению .

Отношение эквивалентности – это отношение "одинаковости" объектов по какому-либо признаку. Например, отношениями эквивалентности являются отношения сонаправленности геометрических векторов, отношение равенства обыкновенных дробей, отношение подобия треугольников и т.п.

Если /=– фактор-множество множества по отношению , то элементыипопавшие в один класс эквивалентности, называются эквивалентными друг другу по отношению:, где "~" – знак эквивалентности.

Примеры.

1. Пусть – множество геометрических векторов на плоскости. Отношениебудет отношением эквивалентности, разбивающим всю плоскость по направлениям, если изисключить нулевой вектор, т.е. образовать множество/. Нуль-вектор считают сонаправленным каждому из векторов плоскости, что нарушает свойство транзитивности. В самом деле, по свойству транзитивности

,

а это означает, что два любых вектора сонаправлены друг другу, что неверно.

2. На множестве всех обыкновенных дробей отношение равенства дробей:, является отношением эквивалентности, разбивающим все множество дробей на классы равных друг другу дробей. Пример такого класса:. Именно классы эквивалентности равных дробей и называют рациональным числом.

3. Пусть ,.

Отношение рефлексивно, так как на главной диагонали матрицывсе элементы – единицы (см. табл. 2.1).- симметричное отношение, поскольку. Найдем.

.

Поскольку,– транзитивное отношение.

На графе этого отношения (см. рисунок) видно, что множество разбито по данному отношению на два непересекающихся классаи.

Если вынуть из графа какое-либо ребро, например, , то отношение перестанет быть симметричным и транзитивным. В самом деле, для парыне найдется симметричной пары, а из того, чтоине будет следовать. Множествоперестанет быть классом эквивалентности, поскольку элементы 1 и 3 отношениемсвязаны не будут.

Нарушение транзитивности произойдет и в том случае, если исключить из графа какую-либо петлю, т.е. нарушить рефлексивность отношения. Исключим, к примеру, петлю . Тогда при выполнения условийизаключениеоказывается ложным.

Определение 2.9. Отношением порядка называют антисимметричное и транзитивное отношение.

Отношение порядка делает множество, на котором оно задано, упорядоченным множеством. Различают частичные порядки и линейные порядки. В частично упорядоченном множестве существуют элементы, не связанные отношением порядка. В линейно упорядоченном множестве каждая пара элементов связана отношением порядка.

Отношениями частичного порядка являются, отношение "делится" во множестве целых чисел, отношения "", "", ">", ">" во множестве n-мерных двоичных векторов, отношение включения в булеане любого множестваи пр.

Отношениями линейного порядка являются отношения "", "", ">", ">" в числовых множествах, отношения "старше", "моложе", "выше", "ниже" во множестве людей и пр.

Пример.

Пусть – множество двумерных двоичных векторов. Покажем, что отношениеявляется отношением частичного порядка. Составим матрицу этого отношения (см. определение (1.5) и формулу (1.3)).

.

Покажем, что и(см. табл. 2.1).

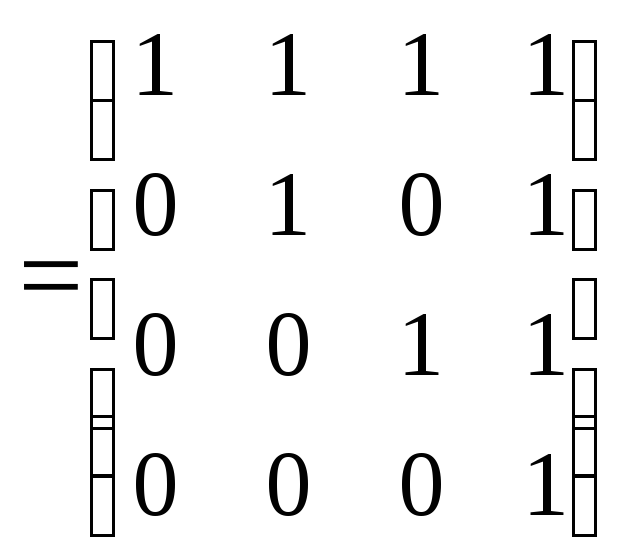
, следовательно, отношениеявляется антисимметричным;

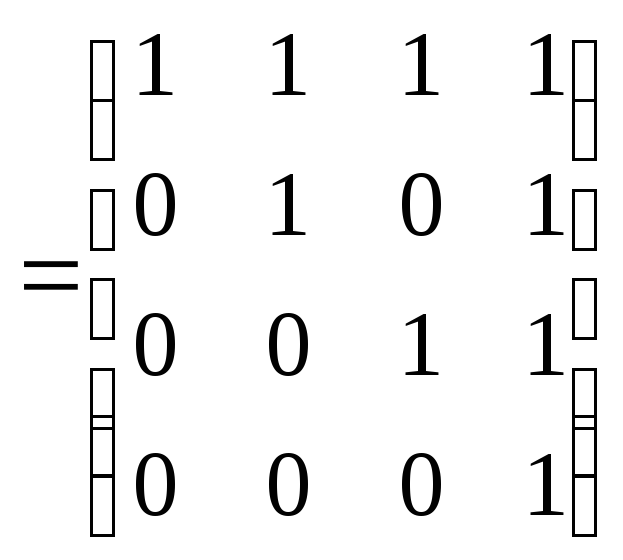
, следовательно,– транзитивное отношение.

Отношение антисимметрично и транзитивно, значит, оно является отношением порядка на множестве. Поскольку некоторые элементы множестване связаны друг с другом этим отношением, например, неравенстваиявляются ложными, то порядок частичный.