2.3. Транзитивность и транзитивное замыкание бинарного отношения

Определение 2.6. Бинарное отношение называюттранзитивным бинарным отношением, если для любых ,ииз того, чтои, вытекает, что.

Символически определение 2.6 записано формулой (2.7).

.

(2.7)

Другими словами, отношение транзитивно, если оно покрывает все опосредованные связи между элементами. Отсюда вытекает, чтоусловием транзитивности отношения является выполнение условия

(2.8)

Используя матрицы отношений, условие (2.8) можно переписать так:

.

(2.9)

Пример.

На множестве ={a,b,c} задано отношение :

.

Покажем, что не является транзитивным отношением.

,

инесравнимы между собой, следовательно, не транзитивно.

Найдем более высокие степени отношения , т.е. матрицы отношений,,,…,:

,

,

,

.

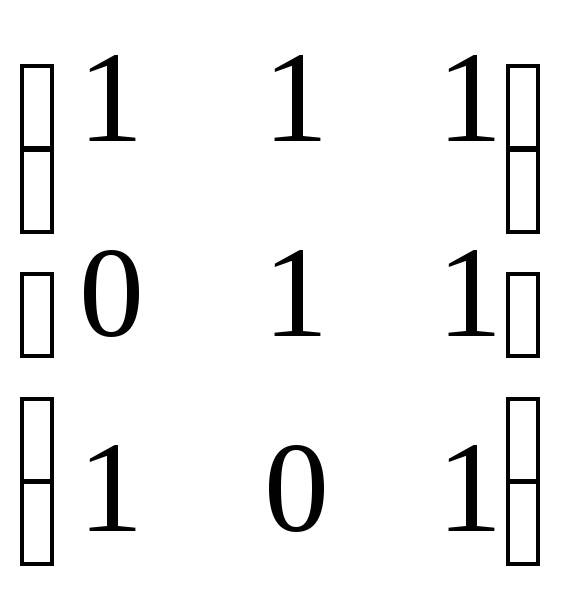
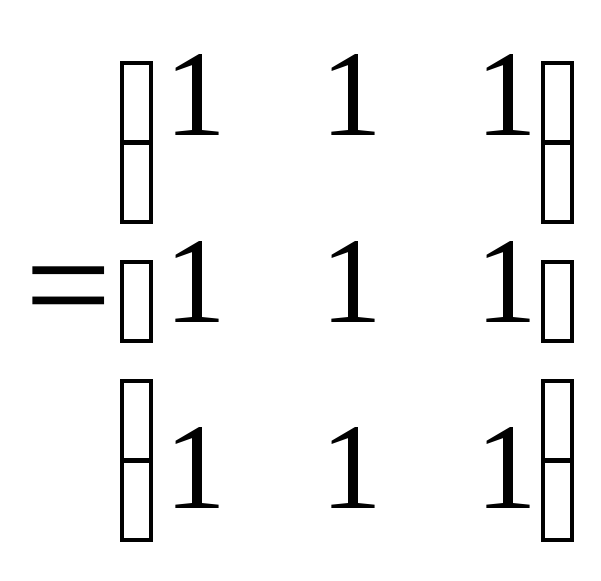Легко проверить, что …=.

Определение 2.7. Транзитивным замыканием бинарного отношения называют объединение степеней этого бинарного отношения:

.

(2.10)

Т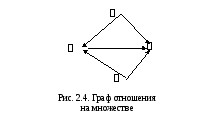ранзитивное замыкание отношения в рассмотренном примере имеет вид.

Пусть на множестве отношениезадано графом (рис.2.4). Запишем матрицуэтого отношения и найдем его транзитивное замыкание.

Матрица отношения .

Для нахождения транзитивного замыкания будем умножать матрицу на себя, получая,,…,, до тех пор, пока не выполнится равенство. Дальнейшее умножение не будет приводить к изменению матриц.

==.

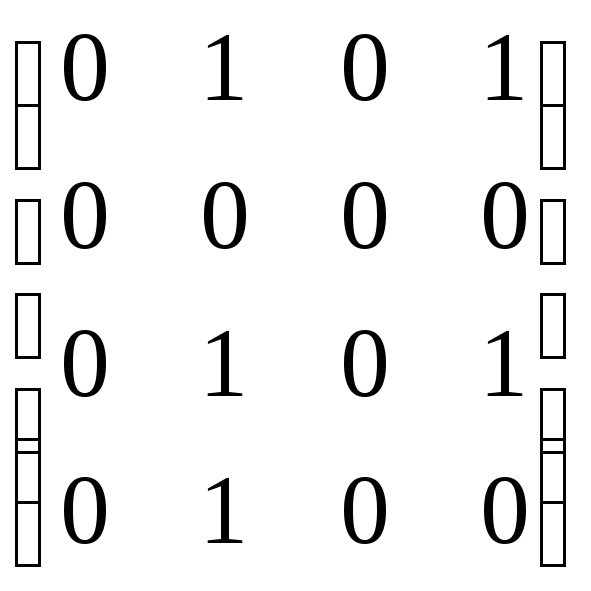Любой элемент матрицы не превосходит соответствующий элемент матрицы, т.е.. Это означает, чтовключает все опосредованные связи между элементами, следовательно,является транзитивным бинарным отношением. Покажем, что его транзитивное замыкание совпадает с самим.

==.

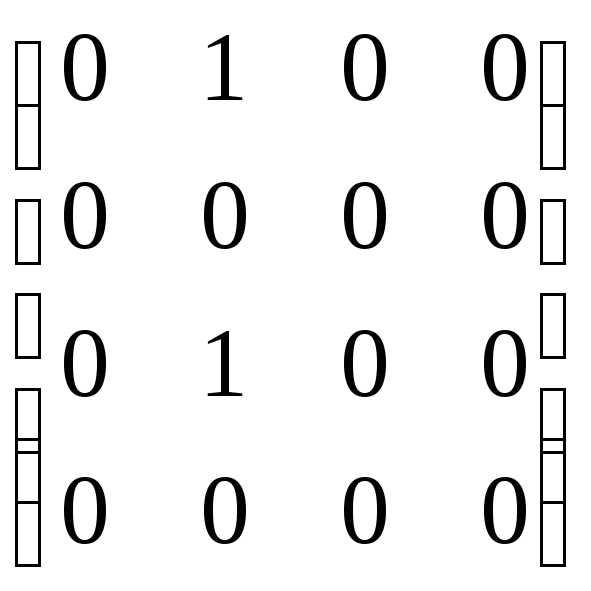
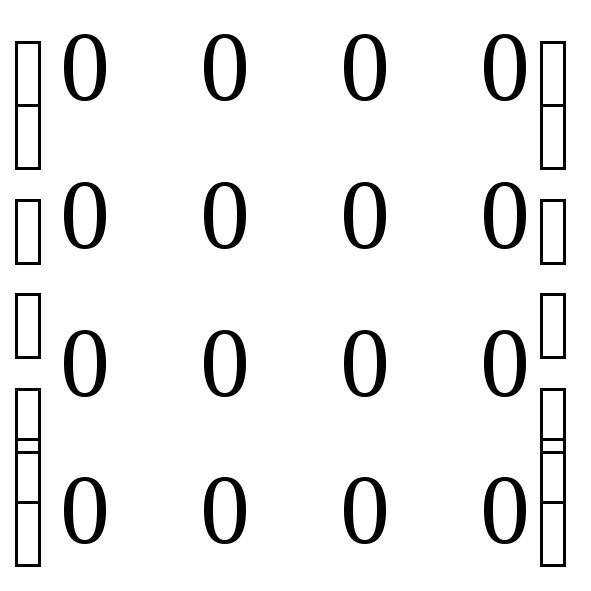
Умножение нуль-матрицы на любую другую матрицу есть нуль-матрица. Поэтому для любых.

Транзитивное замыкание отношения найдем, используя формулу (2.10) и матрицыи:

.

Как и следовало ожидать, поскольку отношение является транзитивным отношением, оно совпадает со своим транзитивным замыканием.

Справедливы следующие утверждения.

Утверждение 1. Транзитивное бинарное отношение совпадает со своим транзитивным замыканием.

Утверждение 2. Транзитивное замыкание бинарного отношения есть наименьшее по числу элементов транзитивное отношение, содержащее данное бинарное отношение.

Утверждение 3. Транзитивное замыкание есть ближайшее к транзитивное отношение.

Использование термина "ближайшее отношение" предполагает, что между отношениями определено расстояние. Для определения расстояния между множествами используют формулу линейного расстояния (формула 2.11), или формулу евклидова расстояния (формула 2.12).

,

(2.11)

,

(2.12)

где – расстояние между подмножествамииуниверсального множества,ихарактеристические функции этих подмножеств. Суммирование выполняется по всем элементам универсального множества.

Для бинарного отношения, заданного на множестве , универсальным множеством является множество. Если, тоназываютполным отношением. Очевидно, что все элементы матрицы полного отношения есть единицы: , где- число элементов множества. Формулы (2.11) и (2.12) для бинарных отношений имеют следующий вид:

,

(2.13)

,

(2.14)

где – число элементов универсального множества,,.

Не следует думать, что последовательность степеней матрицы отношения всегда имеет предел, т. е., начиная с некоторого шага , выполняется равенство. Приведем простой пример, показывающий, что это не так.

Пусть матрица отношения на множествеимеет вид.

Тогда

, ,,….,,

для любого .

Тем не менее .