2.2. Композиция бинарных отношений

Определение 2.5. Композицией бинарных отношений и , заданных на множестве, называют отношениетакое, что

(2.4)

Примечание. В формуле (2.4) использованы символы "", "", "", "". Все эти символы взяты из математической логики, которая рассматривается в главе 4. Однако многим эти символы известны из школьного курса математики. Символназывают квантором всеобщности, он заменяет слова "любой", "всякий", "каждый". Символ– квантор существования, его читают как "существует", "найдется". Символзаменяет слова "…тогда и только тогда…", "…если и только если…", символзаменяет соединительные союзы "и", "а", "но" и пр. Так предложение с этими символами в формуле (2.4) можно прочитать следующим образом: "Для любого элементаиз множестваи любого элементаиз этого же множества справедливо утверждение: паратогда и только тогда, когда во множественайдется такой элемент, чтои".

Если во множестве имеется элемент, через который осуществляется связь между элементамиив композиции отношений, то элементбудем называтьэлементом посредником, а саму связь между и–опосредованной связью.

Пусть ={a,b,c}. Отношения и заданы матрицами:

, .

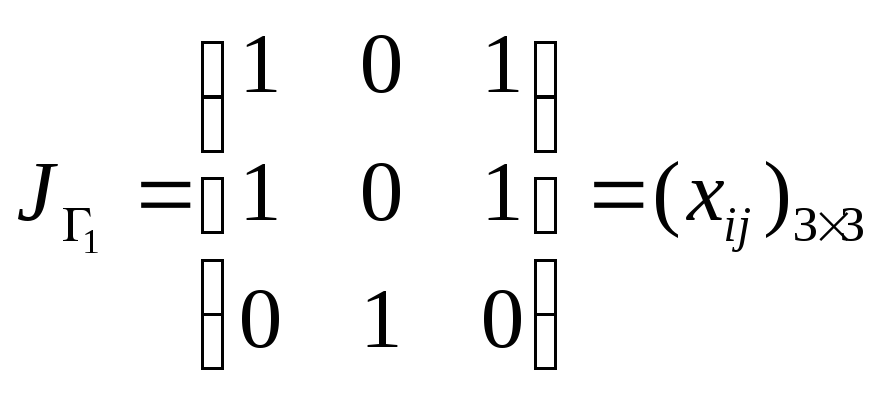Найдем композицию . Для этого выполним следующую последовательность действий:

1) используя матрицы и, запишем графики отношений и :,;

2) построим графы отношений и и объединим их (рис. 2.2);

Примечание1. Графы ипостроены в виде двудольных графов, причем входы графа являются выходами графа .

Примечание 2. Пути в объединении графов иведут от элементов множествак их образам в отношении , и далее к образам в отношении .

3) выпишем все пути, ведущие от элементов a, b и c к их образам в отношении , а также промежуточные элементы в этих путях, посредством которых осуществляются связи в отношении. Результат представим в виде таблицы:

Пути от элементов множества к их образам в отношении	Элементы, осуществляющие опосредованную связь в композиции отношений и	Элементы графика отношения

4) запишем график отношения и построим его граф (рис. 2.3).

Рассмотрим вопрос об отыскании элементов композиции отношений и , не прибегая к графам.

Пусть

, ,– матрицы отношений,и. Задача состоит в том, чтобы найти способ вычисления элементовматрицы.

1. Найдем .

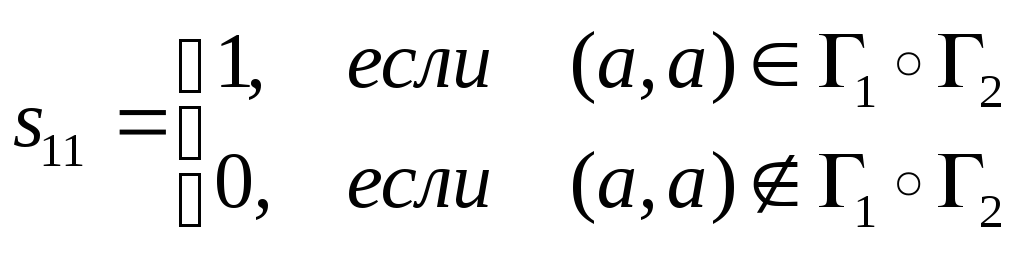, (см. определение 2.4). В свою очередь по формуле (2.4), пара тогда и только тогда, когда во множественайдется такой элемент, чтои. Рассмотрим эти включения для всех возможных значений.

1) ;, так как=1;, так как=0.

Следовательно, не является элементом множества , который осуществляет опосредованную связь междуив композиции отношений. Вывод о том, чтоне является элементом посредником в паре , символически можно записать так:.

2) ;, так как=0;, так как=0.

Следовательно, не является элементом посредником в паре и.

3) ;, так как=1;, так как=1.

Следовательно, осуществляет опосредованную связь в паре и.

Таким образом, во множестве найден элемент, осуществляющий опосредованную связь между элементами парыв композиции отношений. Следовательно,.

Последнее равенство можно рассматривать как результат умножения первой строки матрицы на первый столбец матрицы, в которых умножение элементов матрицы выполняется по правилу логического умножения, а сложение произведений – по правилу операции максимум (см. формулы (1.8), (1.10)).

2. Найдем , воспользовавшись выводом, сделанным в п. 1.

=

=.

Равенство означает, что во множествеесть элемент посредник, осуществляющий связь между элементами парыв композиции отношений. Покажем, что это действительно так.

₁₎ является элементом посредником, посколькуи;

₂₎ не является элементом посредником, так каки;

3) также не является элементом посредником, поскольку, но.

Аналогично находим все элементы матрицы :

=1,

элемент посредник – ;

=1,

элемент посредник – ;

=1,

элемент посредник – ;

=1,

элемент посредник – ;

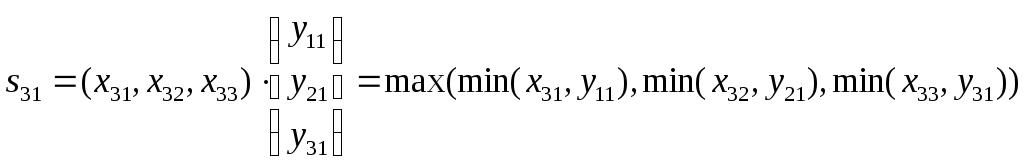=0,

опосредованных связей между инет,;

=0,

опосредованных связей между инет,;

=1,

элемент посредник – .

Таким образом, матрица имеет вид

.

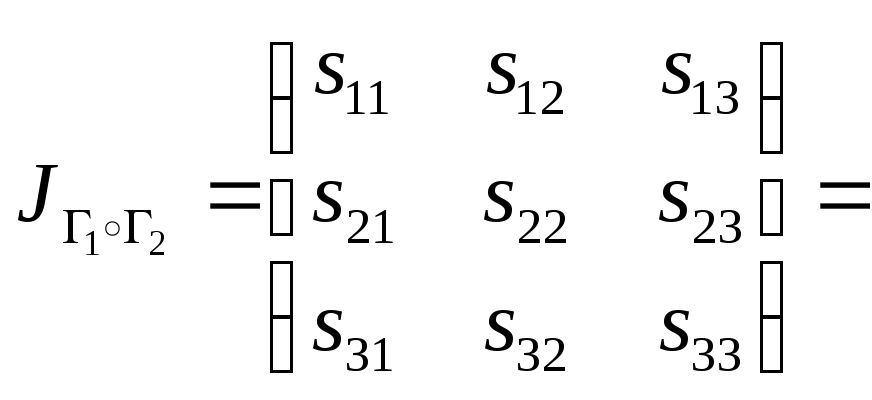
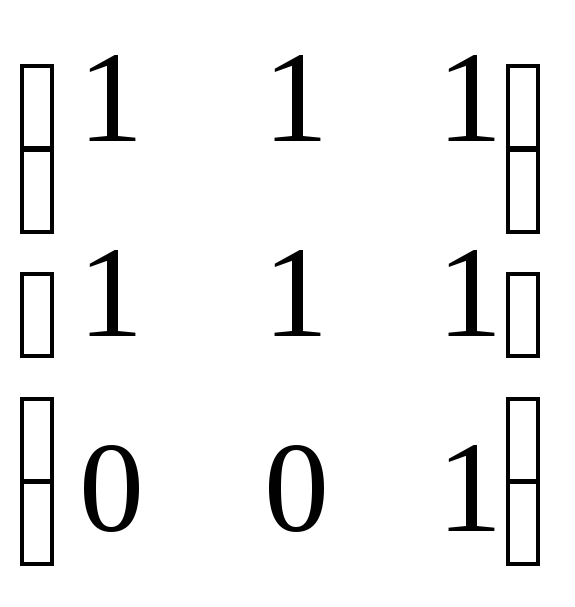Обобщением проделанных операций являются формулы (2.5) и (2.6), которые позволяют вычислять матрицы композиций бинарных отношений на произвольном множестве :

,

(2.5)

где – число элементов множества,– матрица отношения,– матрица отношения,– матрица отношения, элементыкоторой находят по формуле (2.6):

.

(2.6)

Рассмотрим композицию , когда==. В этом случае естественно обозначить=. Учитывая формулу (2.5), получаем:.

Примеры.

1. Пусть и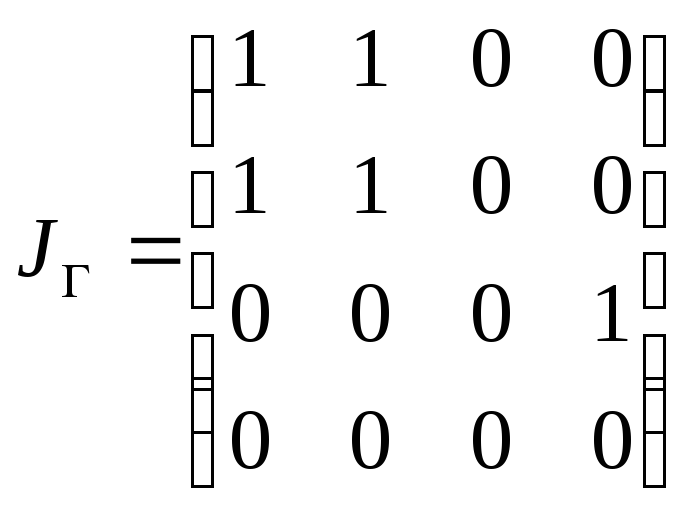– матрица бинарного отношения, заданного на множестве.

Найдем матрицу композиции .

.

Для любой строки матрицыи соответствующей строкиматрицывыполняются неравенства(см. определение (1.5) и формулу (1.3)). Все строки матрицыне меньше отношенующих строк матрицы. Будем считать, что в таком случае. Очевидно, что из неравенстваследует.

В матрице учтены все связи между элементами множества, определяемые отношением, в матрице– все дополнительные опосредованные связи между элементами того же множества. Неравенствоозначает, чтокаждая опосредованная связь покрывается непосредственной связью, т.е. в отношенииучтены все опосредованные связи.

2. , .

.

,,,– строки матрици. Имеем неравенства:,. Строкиинесравнимы между собой.

В матрице записаны все непосредственные связи, определяемые отношением, в матрице– дополнительные опосредованные связи в этом же отношении.

Проанализируем неравенства истрок, соответствующих элементам.

1) означает, что опосредованная связь(– элемент посредник) не покрывается непосредственной связью меду этими элементами в отношении:, но.

2) говорит о том, что связьтолько непосредственная, элемент посредник, осуществляющий эту связь в композиции отношений, отсутствует:, но.

3) , означает, что связьявляется только опосредованной (– элемент посредник):, но.

Таким образом, если строки иматрицинесравнимы или, то опосредованные связи между элементами множества покрываются непосредственными связями лишь частично или не покрываются совсем.

Из рассмотренных примеров делаем вывод.

Вывод. Если в отношении непосредственные связи между элементами множествапокрывают все опосредованные связи между его элементами, тои.