
Пу-112 КТэ 2 сем / Математика / Словарь
.doc
ГЛОССАРИЙ
К разделу «Линейная алгебра и аналитическая геометрия»
курса «МАТЕМАТИКА»
(ГОС 2000)
для студентов заочной формы обучения специальности
060800 - Экономика и управление на предприятии (машиностроение)
Екатеринбург 2005
|
Термин |
Обозначение |
Определение и пояснения |
|
|
Алгебра линейная |
|
|
|
|
Аксиомы линейной алгебры |
- |
Аксиомы сложения:
|
Аксиомы умножения на число:
|
|
Вектор |
|
Основное, неопределяемое понятие линейной алгебры, элемент множества, в котором определены линейные операции. |
|
|
Линейные операции над векторами |
- |
Умножение вектора на число и сложение векторов. |
|
|
Вектор арифметический |
|
Последовательность чисел, координат вектора, записанная либо строкой (вектор-строка), либо столбцом (вектор-столбец) |
|
|
Размерность арифметического вектора |
- |
Число координат вектора. |
|
|
Нуль-вектор арифметический |
|
Арифметический вектор, все координаты которого – нули. |
|
|
Умножение на число арифметического вектора |
|
Умножение на число x каждой координаты вектора. |
|
|
Сложение арифметических векторов одинаковой размерности |
|
Сложение соответствующих координат векторов. |
|
|
Векторы арифметические коллинеарные |
|
Векторы
|
|
|
Векторы арифметические противонаправленные |
|
Коллинеарные
векторы, для которых
|
|
|
Векторы арифметические противоположные |
|
Противонаправленные
векторы, для которых
|
|
|
Векторы арифметические равные |
|
Векторы, состоящие из одинаковых координат. |
|
|
Векторы арифметические сонаправленные |
|
Коллинеарные
векторы, для которых
|
|
|
Скалярное произведение арифметических векторов |
|
Действительное число, сопостовляемое каждой паре векторов одинаковой размерности, и удовлетворяющее следующим аксиомам:
При
ортонормированном базисе вычисляется
по формуле:
|
|
|
Норма (длина) арифметического вектора |
|
Неотрицательное
действительное число, сопостовляемое
вектору. В евклидовых пространствах
с ортонормированным базисом вычисляется
по формуле:
|
|
|
Ортогональные арифметические векторы |
- |
Векторы одинаковой размерности, скалярное произведение которых равно нулю. |
|
|
Евклидово пространство |
- |
Векторное пространство, в котором определено скалярное произведение |
|
|
|
|
|
|
|
|
|
|
|
|
Вектор геометрический |
|
Направленный отрезок; отрезок, имеющий начало и конец. |
|
|
Векторы геометрические коллинеарные |
|
Направленные отрезки, лежащие на одной прямой или на параллельных прямых. |
|
|
Векторы геометрические противонаправленные |
|
Коллинеарные геометрические векторы, лежащие в разных полуплоскостях, на которые разбивает плоскость прямая, проведенная через их начала. |
|
|
Векторы геометрические равные |
|
Сонаправленные геометрические векторы, одинаковой длины. |
|
|
Векторы геометрические сонаправленные |
|
Коллинеарные геометрические векторы, лежащие в одной полуплоскости, границей которой является прямая, проведенная через их начала. |
|
|
Вектор геометрический свободный |
|
Множество равных друг другу направленных отрезков. |
|
|
Единичный геометрический вектор |
|
Направленный отрезок, длина которого равна единице длины. |
|
|
Длина геометрического вектора |
|
Длина направленного отрезка. |
|
|
Нуль-вектор геометрический |
|
Вектор нулевой длины, точка. |
|
|
Умножение геометрического вектора на число |
|
Операция,
сопоставляющая заданным числу
1. 2.
|
|
|
Сложение геометрических векторов |
|
Операция, сопоставляющая двум заданным геометрическим векторам третий вектор, который находят по правилу треугольника или правилу параллелограмма. |
|
|
Правило треугольника |
- |
Приложить
вектор |
|
|
Правило параллелограмма |
- |
Приложить
векторы
|
|
|
Скалярное произведение геометрических векторов |
|
Число,
равное произведению длин векторов
на косинус угла между ними:
|
|
|
Векторное произведение геометрических векторов |
|
Вектор, длину и направление которого находят по следующему правилу:
|
|
|
Компланарные векторы |
|
Векторы, лежащие в одной плоскости или параллельных плоскостях. |
|
|
Правая тройка векторов, левая тройка векторов |
|
Пусть
|
|
|
Смешанное произведение геометрических векторов |
|
|
|
|
Векторное пространство |
Vn, Rn |
Множество геометрических или арифметических векторов, замкнутое относительно операций умножения на число и сложения |
|
|
Система векторов |
( |
Последовательность векторов какого-либо векторного пространства |
|
|
Линейная комбинация векторов |
- |
Вектор
вида:
|
|
|
Нулевая линейная комбинация векторов |
- |
Линейная комбинация векторов, равная нуль-вектору. |
|
|
Вырожденная линейная комбинация векторов |
- |
Линейная комбинация векторов, в которой все числовые коэффициенты равны нулю. |
|
|
Линейно независимая система векторов |
- |
Система векторов, единственная нулевая комбинация которых вырожденна. |
|
|
Свободная система векторов |
- |
Другое название линейно независимой системы векторов. |
|
|
Линейно зависимая система векторов |
- |
Система векторов, которая помимо вырожденной имеет другие (невырожденные) нулевые линейные комбинации |
|
|
Максимальная свободная система векторов пространства |
- |
Свободная система векторов, добавление к которой любого вектора пространства делает ее линейно зависимой. |
|
|
Базис векторного пространства |
- |
Максимальная линейно независимая система векторов векторного пространства. |
|
|
Размерность векторного пространства |
- |
Число векторов в максимальной свободной системе векторов этого пространства. |
|
|
Разложение вектора по базису |
- |
Представление вектора в виде линейной комбинации базисных векторов. Такое представление при фиксированном базисе единственно. |
|
|
Векторы базисные |
( |
Векторы, составляющие выбранный базис векторного пространства. |
|
|
Ортонормированный базис |
- |
Базис, все векторы которого попарно ортогональны и имеют длину (норму) равную единице. В пространствах геометрических векторов ортонормированные базисы имеют обозначения: ( |
|
|
Числовая ось |
Ox, Oy, Oz…. |
Прямая,
к одной из точек которой приложен
единичный вектор. Точку O,
к которой приложен единичный вектор,
называют началом числовой оси. Каждой
точке P
числовой оси соответствует определенное
действительное число x,
равное
|
|
|
Проекция точки M на прямую |
M’ |
Основание перпендикуляра к прямой, проходящего через точку M, |
|
|
Проекция вектора (геометрического) на ось |
|
Пусть
|
|
|
Проекции вектора (геометрического) на вектор, |
|
Проекция
вектора
|
|
|
Проекция вектора (геометрического) на плоскость |
|
Вектор
|
|
|
Орт вектора |
|
Вектор
единичной длины, сонаправленный
|
|
|
Система координат |
- |
Способ установления взаимно однозначного соответствия между пространствами геометрических и арифметических векторов одинаковой размерности. |
|
|
Декартова прямоугольная система координат |
- |
Ортонормированный
базис
|
|
|
Линейная оболочка системы векторов |
- |
Множество всех линейных комбинаций этих векторов. |
|
|
Линейное подпространство пространства Rn |
- |
Подмножество множества Rn, замкнутое относительно линейных операций. |
|
|
Сумма линейных подпространств L1 и L2 пространства Rn |
L1+L2 |
Подмножество множества Rn, состоящее из всех сумм векторов пространств L1 и L2. |
|
|
Пересечение линейных подпространств L1 и L2 пространства Rn |
|
Подмножество множества Rn, состоящее из всех общих векторов пространств L1 и L2. |
|
|
Объединением линейных подпространств L1 и L2 пространства Rn |
|
Подмножество множества Rn, состоящее из всех векторов, принадлежащих пространству L1 или пространству L2. |
|
|
Матрица,
размерности p |
|
Прямоугольная таблица чисел, состоящая из p строк и q столбцов. |
|
|
элемент матрицы |
|
Число, принадлежащее матрице, стоящее в i-той строке и j-том столбце. |
|
|
Транспонированная матрица |
|
Матрица,
полученная из матрицы
|
|
|
Квадратная матрица |
|
Матрица, в которой число строк равно числу столбцов. |
|
|
Порядок квадратной матрицы |
- |
Число строк или число столбцов квадратной матрицы. |
|
|
Главная диагональ матрицы |
- |
Диагональ,
идущая сверху вниз и слева направо,
проходящая через элементы
|
|
|
Побочная диагональ квадратной матрицы |
- |
Диагональ,
идущая сверху вниз и справа налево,
проходящая через элементы
|
|
|
Единичная матрица |
|
Квадратная матрица порядка n, по главной диагонали которой стоят единицы, а все остальные числа – нули. |
|
|
Диагональная матрица |
- |
Квадратная матрица, по главной диагонали которой стоят числа, отличные от нуля, а все остальные – нули. |
|
|
Верхнетреугольная матрица |
- |
Квадратная матрица, на главной диагонали которой стоят числа, отличные от нуля, выше главной диагонали – числа не все равные нулю, ниже главной диагонали - все числа равны нулю |
|
|
Нижнетреугольная матрица |
- |
Квадратная матрица, на главной диагонали которой стоят числа, отличные от нуля, ниже главной диагонали – числа не все равные нулю, выше главной диагонали - все числа, равные нулю. |
|
|
Равенство матриц |
|
Матрицы
одинаковой размерности, для которых
выполняется равенство:
|
|
|
Умножение матрицы на число |
|
Умножение на число каждого элемента матрицы |
|
|
Сложение матриц |
|
Сложение соостветствующих элементов матриц. |
|
|
Подматрица. |
- |
Часть
матрицы
|
|
|
Произведение матриц |
|
Матрица
|
|
|
Коммутирующие матрицы |
- |
Матрицы,
для которых выполняется равенство: |
|
|
Обратная матрица
|
|
Матрица,
для которой выполняются равенства:
|
|
|
Определитель матрицы второго прядка |
|
Числовая
характеристика матрицы второго
порядка, вычисляемая по правилу:
|
|
|
Минор |
|
Определитель квадратной подматрицы. |
|
|
Алгебраическими дополнениями элемента матрицы A |
|
|
|
|
Присоединенная матрица |
|
Матрица, элементами которой являются алгебраические дополнения матрицы AT. |
|
|
Элементарные преобразования строк (столбцов) матрицы |
- |
Следующие операции над строками (столбцами) матрицы:
|
|
|
Эквивалентные матрицы |
|
Матрицы, полученные одна из другой путем элементарных преобразований. |
|
|
Ранг матрицы |
|
Число линейно независимых строк (столбцов) матрицы. |
|
|
Система линейных алгебраических уравнений (СЛАУ) |
- |
Система
равенств, вида:
|
|
|
Решение СЛАУ |
- |
Набор значений неизвестных, при подстановке которых в систему все равенства системы становятся верными числовыми равенствами. |
|
|
Несовместная СЛАУ |
- |
СЛАУ, не имеющая решений. |
|
|
Равносильные |
- |
СЛАУ, все решения которых одинаковы. |
|
|
Формулы Крамера |
- |
Формулы
вычисления решения совместной СЛАУ
с квадратной матрицей:
|
|
|
Метод Гаусса решения СЛАУ |
- |
Решение
СЛАУ последовательным выполнением
прямой и обратной процедур Гаусса.
Прямая процедура - сведение путем
элементарных преобразований расширенной
матрицы системы
|
|
|
Однородная СЛАУ |
- |
Система,
столбец свободных членов которой
состоит из нулей: |
|
|
Базисные переменные |
- |
Переменные СЛАУ, соответствующие единичной матрице после прямой процедуры Гаусса. |
|
|
Свободные переменные |
- |
Переменные СЛАУ, не являющиеся базисными. |
|
|
Общее решение СЛАУ. |
- |
Множество
всех решений СЛАУ в случае, когда ранг
главной матрицы системы r
равен рангу расширенной матрицы
системы, но меньше числа неизвестных
n.
Общее решение включает в себя
произвольные константы
|
|
|
Частное решение СЛАУ |
- |
Решение СЛАУ, полученное из общего решения путем придания значений произвольным константам. |
|
|
Фундаментальная система решений однородной СЛАУ. |
- |
Система
столбцов
|
|
|
Отображение множества X во множество Y |
- |
Правило или закон, по которому каждому элементу множества X поставлен в соответствие определенный (единственный) элемент множества Y. |
|
|
Линейный
оператор, действующий на пространстве
|
|
закон
|
|
|
матрица
линейного оператора
|
|
матрица |
|
|
Сумма
линейных операторов
|
|
линейный
оператор такой, что
|
|
|
Произведение
оператора
|
α |
оператор
(α |
|
|
Произведение
оператора
|
|
оператор
|
|
|
Собственный
вектор оператора
|
- |
называют
ненулевой вектор
.
|
|
|
Собственное
направление оператора
|
- |
все
векторы
|
|
|
Собственное
значение оператора
|
- |
число
|
|
|
характеристическим
уравнением матрицы
|
|
Уравнение для нахождения собственных значений матрицы A. |
|
|
Репер или система координат в пространстве |
|
упорядоченный
набор
|
|
|
Радиус-вектор
точки
|
|
вектор
|
|
|
Общее уравнение плоскости |
|
уравнение
вида:
|
|
|
общее уравнение прямой на плоскости. |
|
уравнение
вида:
|
|
|
общее уравнение прямой |
|
Система
равенств вида:
|
|
|
ортогональной матрицей. |
|
Матрица
|
|
|
симметрическим или самосопряженным оператором |
|
Линейный
оператор
|
|
|
Квадратичная
форма в пространстве
|
|
однородный многочлен с действительными коэффициентами от координат переменного вектора, то есть выражение:
|
|
|
матрица квадратичной формы |
|
матрица коэффициентов квадратичной формы, симметрична, относительно главной диагонали:
|
|
|
приведение квадратичной формы к главным осям. |
|
нахождение базиса, в котором квадратичная форма превращается в сумму квадратов своих переменных.
|
|
|
Кривая второго порядка на плоскости |
|
линия,
уравнение которой в заданной системе
координат имеет вид:
|
|
|
Эллипс |
|
плоская
замкнутая кривая, сумма расстояний
|
|
|
Каноническое уравнение эллипса |
|
Уравнение
вида:
|
|
|
Гипербола |
|
плоская
кривая, модуль разности расстояний
|
|
|
Каноническое уравнение гиперболы |
|
Уравнение
вида:
|
|
|
Парабола |
|
плоская
кривая, расстояние
|
|
|
Каноническое уравнение параболы |
|
Уравнение
вида:
|
|
|
Поверхность второго порядка |
|
линия,
уравнение которой в заданной системе
координат имеет вид:
|
|
|
Эллипсоид |
|
поверхность,
каноническое уравнение которой имеет
вид:
|
|
|
Однополостный гиперболоид |
|
поверхность,
каноническое уравнение которой имеет
вид:
|
|
|
Двуполостный гиперболоид |
|
поверхность,
каноническое уравнение которой имеет
вид:
|
|
|
Эллиптический параболоид |
|
называют
поверхность, каноническое уравнение
которой имеет вид:
|
|



 .
.
 ,
где
,
где
 числовая матрица,
числовая матрица,
 - вектор столбец чисел,
- вектор столбец чисел,
 - вектор столбец переменных.
- вектор столбец переменных.
 такая, что
такая, что
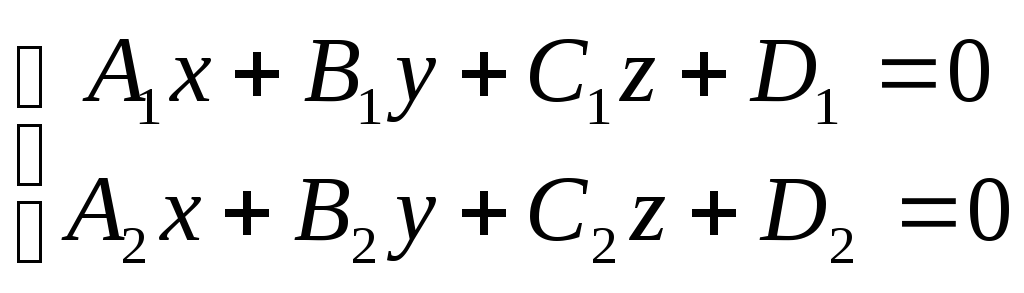 .
. .
.