Раздел 5. Линейные векторные пространства.

Задача 1.Выяснить, является ли линейным пространством множество всех матриц второго порядка вида(*), где?

Множество указанных матриц является линейным пространством, если в этом множестве определены операции сложения элементов и умножения элемента на число, удовлетворяющие свойствам.

Введем следующие обозначения:

,, где.

Заметим, что операция сложения в этом множестве определена, поскольку рассматриваются квадратные матрицы одного порядка (второго), кроме того, результат сложения – матрица такого же вида.

Проверим коммутативность и ассоциативность сложения таких матриц.

Действительно, на основании коммутативности сложения во множестве действительных чисел имеем:

.

Аналогично, на основании ассоциативности сложения во множестве , получается ассоциативность сложения исследуемых матриц.

Заметим, что в выполнении этих свойств можно было убедиться, используя аналогичные свойства сложения матриц.

В качестве нулевого элемента укажем нулевую матрицу , для которой, очевидно, выполняется свойство:, где- матрицы из исследуемого множества. В качестве противоположного элемента для каждой матрицы вида (*) выберем матрицу, тогда.

Необходимые свойства операции умножения на число следуют из справедливости аналогичных свойств этой операции над матрицами. Отметим только, что результат – снова матрица вида (*), поскольку при умножении элементов второй строки на любое вещественное число они не изменятся (свойство нуля во множестве ), а при умножении элементов первой строки – результат будет снова вещественным числом.

Таким образом, линейные операции удовлетворяют аксиомам линейного пространства, что означает, что множество матриц вида (*) является линейным пространством.

Задача 2. Выяснить, является ли данная система векторов излинейно зависимой?

Для того чтобы указанная система векторов была линейно зависимая, необходимо существование таких чисел, не равных одновременно нулю, что будет выполняться векторное равенство:

.

Для нахождения чисел распишем векторное равенство в координатной форме, в результате чего получим систему линейных уравнений:

.

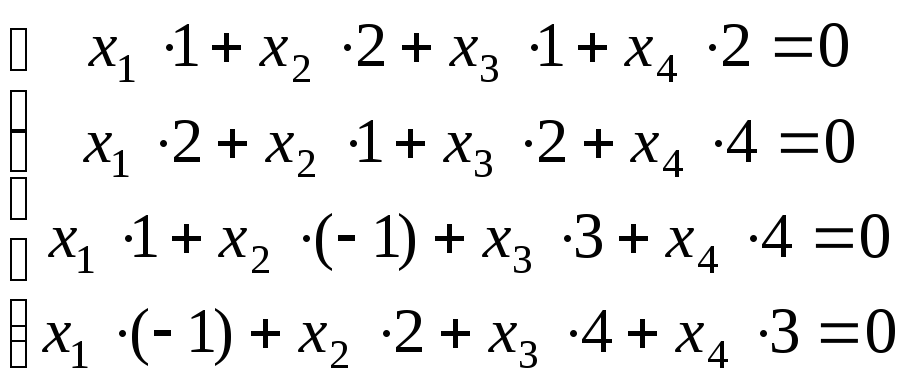Решим систему методом Гаусса:

Поскольку ранг матрицы (r=3) меньше числа переменных (n=4), то однородная система линейных уравнений имеет бесконечное множество решений (), что и означает линейную зависимость системы векторов.

Замечание. Задачу 2 можно было решить и иначе, используя тот факт, что однородная система неопределенна в случае, если определитель матрицы системы равен нулю. В противном случае, т.е. когда определитель матрицы системы отличен от нуля, система была бы определенна и имела бы только нулевое решение, что означало бы линейную независимость векторов.

Таким образом, линейную зависимость векторов можно проверять, вычисляя определитель, составленный из координат этих векторов.

Задача 3. Даны векторыв некотором базисе. Показать, что векторыобразуют базис и найти координаты векторав этом базисе.

Для того чтобы показать, что векторыобразуют базис вычислим определитель, составленный из координат векторов:

Значит, векторы образуют базис.

Определим координаты вектора в этом базисе, т.е. найдем такие числа, что.

Расписывая последнее соотношение в координатной форме, получаем систему линейных уравнений:

Решая систему методом Гаусса, получаем:

.

Таким образом, система принимает вид:

откуда

Таким образом, координаты векторав базисеследующие:.

Задача 4. Найти все значения, при которых векторлинейно выражается через векторы, если.

Согласно условию,есть линейная комбинация, т.е.

или в координатной форме:

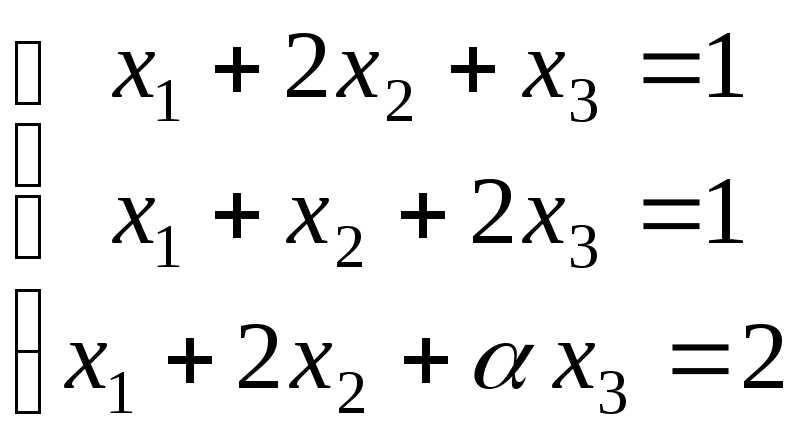, где- неизвестные числа, не равные одновременно нулю.

Решим полученную систему линейных уравнений методом Гаусса:

.

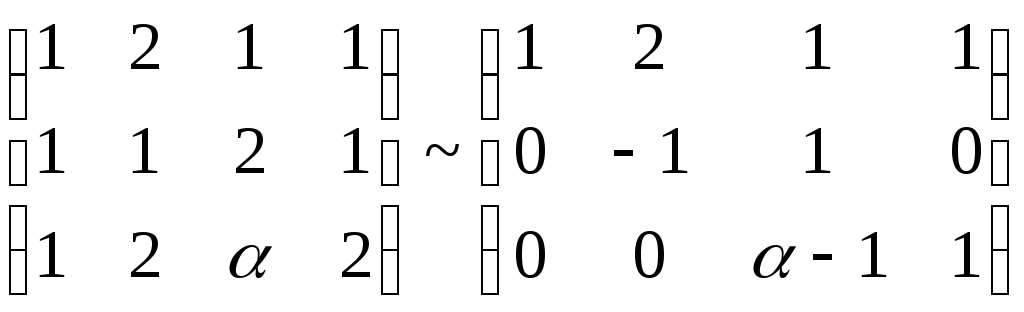
Поскольку система линейных уравнений совместна только в случае, когда ранг матрицы системы совпадает с рангом расширенной матрицы, то рассматриваемая система будет совместна при. В противном случае, ранг матрицы системы равен 2, а ранг расширенной матрицы равен 3, а значит, система будет несовместна.

Задача 5. Показать, что система арифметических векторов,,,,образует базис ви найти координаты вектора.

Векторыобразуют базис, если они линейно независимы. Поэтому, используя замечание к задаче 2, вычислим определитель, составленный из координат векторов:

. При вычислении определителя использовали свойство: определитель треугольного вида равен произведению диагональных элементов.

Таким образом, векторы образуют базис в.

Тогда любой вектор можно представить в виде линейной комбинации базисных векторов, т.е.

, где- неизвестные числа, не равные одновременно нулю, причем, числаявляются координатами векторав базисе.

Запишем последнее равенство в координатной форме:

или

Решая подстановкой последнюю систему линейных уравнений, получаем:

.

Таким образом, координаты векторав базисеимеют вид:(-1;3;-3;3;-3).