4.2. Плоскость в пространстве.

Задача 4.Составить уравнение плоскости, проходящей через точку, параллельную плоскости3x+2y-z+1=0.

Воспользуемся уравнением плоскости, перпендикулярной данному векторуи проходящей через точку:.

Поскольку плоскостьпараллельна плоскости3x+2y-z+1=0, вектор нормаликоторой определяется коэффициентами передx, y,z, т.е. , то в качестве вектора, перпендикулярного плоскостиможно взять именно этот вектор. Таким образом, уравнение плоскостиимеет вид:или3х+2у-z-17=0.

Задача 5.Составить уравнение плоскости, которая проходит через точкуперпендикулярно двум плоскостям:x-3y+2z+1=0и

: 2x+y-2z+5=0.

Воспользуемся уравнением плоскости, перпендикулярной данному векторуи проходящей через точку:. Но сначала найдем вектор.

По общим уравнениям плоскостей и определим векторы нормалей этих плоскостей, а именно,и.

Поскольку по условию плоскость перпендикулярна плоскостями , то нормальный векторплоскостиперпендикулярен векторами. Поэтому в качестве нормального вектора можно взять вектор, равный векторному произведению этих векторов (поскольку, по определению, векторное произведениеперпендикулярно и векторуи вектору), т.е.

.

Откуда =(4;6;7).

Таким образом, получаем уравнение плоскости :

4(x-2)+6(y-(-1))+7(z-(-1))=0или4(х-2)+6(у+1)+7(z+1)=0.

Т.е. 4х+6у+7z+5=0.

Задача 6. Найти расстояниеdточкидо плоскости2x-y-2z+5=0.

Расстояниеdнайдем по формуле:

d =.

Задача 7. Уравнение плоскости, проходящей через точкиА(2;4;3),В(6;3;1),С(3;3;4).

Воспользуемся уравнением плоскости, проходящей через три точки. Получаем:

.

.

Раскладываем определитель по первой строке:

или

(х-2)(-1-2)-(у-4)(4+2)+(z-3)(-4+1)=0,

-3(х-2)-6(у-4)-3(z-3)=0,

-3x+6-6y+24-3z+9=0,

-3x-6y-3z+39=0 /(-3)

x+2y+z-13=0 –уравнение плоскостиАВС.

4.3. Прямая в пространстве.

Задача 8.Составить канонические и параметрические уравнения прямойl, проходящей через точкупараллельно:

а) прямой ;

б) осиОх.

а) Составим канонические уравнения прямой l:, где- точка прямойl,

- направляющий вектор прямойl, т.е. вектор, лежащий на прямой, параллельнойl, или на самой прямой l .

Поскольку прямая lпараллельна прямой, то направляющий вектор этой прямой(3;-1;2)будет направляющим и для прямойl.

Поэтому канонические уравнения прямой lтаковы:

или.

Из канонических уравнений прямой lполучим параметрические уравнения. Введем обозначения:.

Из последнего соотношения получаем уравнения:

или- параметрические уравнения прямойl.

б) Поскольку прямая параллельна оси Ох, то в качестве направляющего вектора выберем единичный вектор, лежащий на осиОх, -. Тогда канонические уравнения искомой прямой имеют вид:.

Аналогично предыдущему пункту данной задачи составим параметрические уравнения:

,

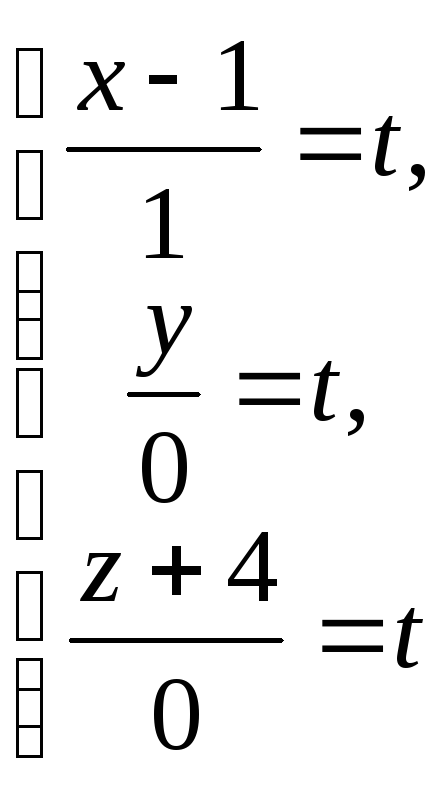или- параметрические уравнения искомой прямой.

Задача 9. Составить канонические уравнения прямойl

.

Для составления канонических уравнений прямойlнеобходимо знать точку- точку прямойlи- направляющий вектор прямойl.

Из заданных уравнений прямой l

найдем координаты точки.

Для этого, поскольку неизвестных – три, а уравнений в системе лишь два, придадим одной из неизвестных конкретное значение, например, х=0. Тогда система принимает вид:или. Решая систему, получаем:

y-3z=1 3

-3y+z=5 1

-8z=8, z=-1, y=1+3z=1-3=-2.

Итак, .

Далее, поскольку прямая l, согласно условию, - есть пересечение плоскостей5х+y-3z-1=0и 2x-3y+z-5=0, т.еl принадлежит каждой плоскости,то нормальные вектораиэтих плоскостей перпендикулярны прямойl. А значит, в качестве направляющего вектора возьмем векторное произведениеи, т.е.:

т.е.. Тогда параметрические уравнения прямой имеют вид:или.