2.3. Однородные системы линейных уравнений.

Однородные системы линейных уравнений всегда имеют решение, по крайней мере, нулевое. Поэтому однородная система либо имеет единственное (нулевое) решение, либо бесконечное множество решений. Причем, если , то система имеет единственное, нулевое решение, если, то система имеет бесконечное множество решений.

Задача 4. Решить систему уравнений:

.

Приведем матрицу системы к ступенчатому виду, используя, например, алгоритм метода Гаусса:

~~.

Поскольку , то система имеет бесконечное множество решений. Главная матрица системы имеет вид:. Поэтому в качестве базисных переменных выберем, тогда- свободная, и пусть.

В результате, система уравнений принимает вид:

или ,

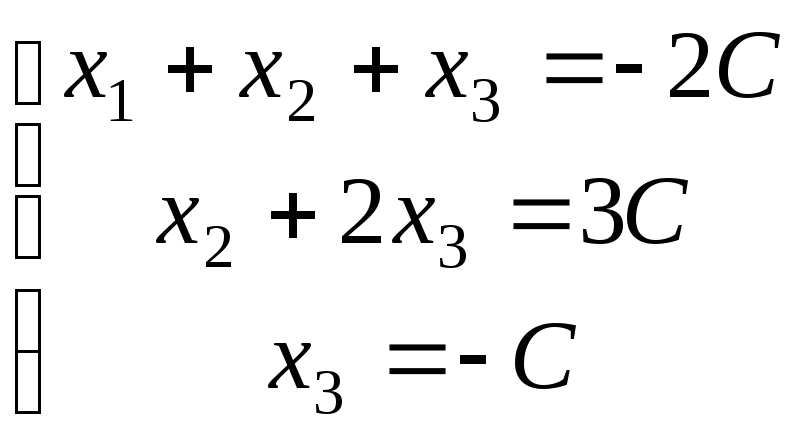откуда ,

.

Таким образом,или.

Задача 5. Решить систему уравнений:

.

Приведем матрицу системы

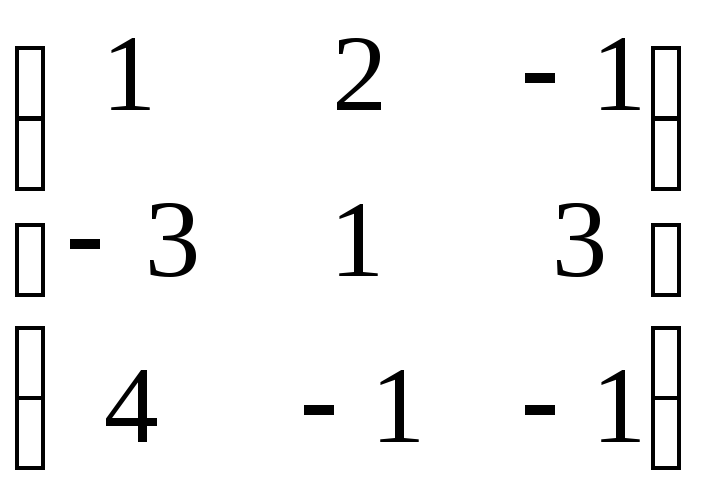
к диагональному виду, используя правило прямоугольника.

Шаг 1. Разрешающий элемент . Тогда матрица примет вид:

Шаг 2. Разрешающий элемент .

.

Шаг 3. Разрешающий элемент . Тогда окончательная матрица принимает вид:

. Значит, решением однородной системы (ранг которой совпадает с числом неизвестных) является единственное нулевое решение: .

Раздел 3. Векторная алгебра.

Формулы, использованные при решении задач данного раздела приведены в главе 2 теоретической части. Добавим лишь, что при вычислении векторного и смешанного произведения векторов формулы, указанные в главе 2, можно записать иначе, используя определители.

Так, вычисляя векторное произведение векторов , далее будем использовать формулу:

(1).

А при вычислении смешанного произведения векторов иследующую формулу:

(2).

Задача 1. Даны вершины треугольникаАВС:А(1;-1;2), В(2;1;0), С(6;3;4). Найти:

1. векторы ;

2. скалярное произведение ;

3. длины сторон треугольника;

4. величину угла А;

5. проекцию вектора на направление вектора;

6. векторное произведение и его модуль;

7. площадь треугольника АВС;

8. длину высоты, опущенной из вершины А.

1. Координаты указанных векторов найдем, вычитая из координат конца координаты начала вектора:, т.е.;;.

2. Скалярное произведение векторов, заданных в прямоугольной системе координат, равно сумме произведений их одноименных координат (см. формулу 2.13 теоретической части):

.

3. Для определения длин сторон необходимо найти длины соответствующих векторов: . Применяя формулу 2.6., получаем:

,,

.

4. Угол Аесть угол между векторами.

Вычислим косинус угла между указанными векторами по формуле:

,.

Значит, .

5. Проекцию вектора на направление векторавычисляем по формуле:

.

6. Векторное произведение вычислим по формуле (1), раскладывая определитель по первой строке:

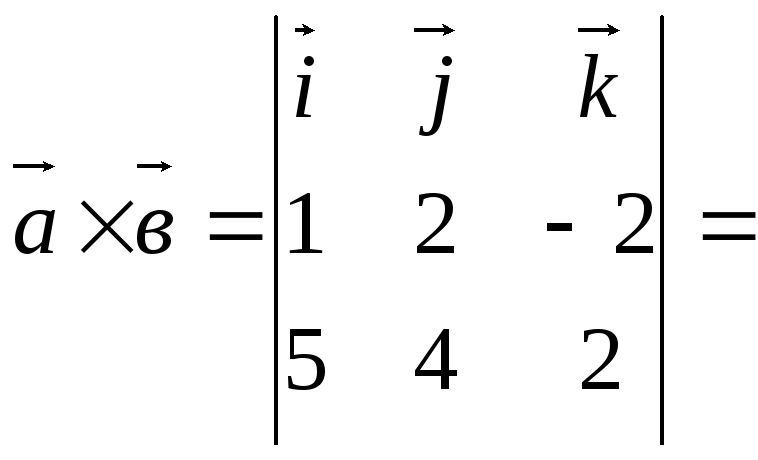
Найдем модуль векторного произведения:.

7. Площадь SтреугольникаАВСвычислим по формуле:.

В нашем случае, (кв.ед.).

8. В пункте 7 мы нашли площадь треугольника АВС,(кв.ед.), с другой стороны, известно, что площадь треугольника равна половине произведения основания на высоту, опушенную к этому основания.

Внашем случае,, гдеАН– искомая высота. Из последней формулы ее можно выразить так:(ед.), гдеВС=6найдено в пункте 3 нашей задачи.

Задача 2. Вычислить смешанное произведение векторов,,.

Запишем координаты векторов, учитывая их разложение по ортам ,,. Тогда смешанное произведениеэтих векторов равно определителю, составленному из координат первого, второго и третьего векторов (формула (2)):

Итак,.

Задача 3. Вычислить объем пирамиды, вершины которойА(1;2;1),

В(-2;3;-3), С(1;3;3), D(2;1;-3).

Объем пирамиды вычислим, используя одно из свойств смешанного произведения: объем Vпирамиды, построенной на векторах, равен

V=. Поэтому определим сначала векторы, а затем найдем их смешанное произведение.

В качестве векторов выберем векторы, исходящие из точкиА:

,.

,

,.

.

ТогдаV=