Практикум

Раздел 1. Матрицы и определители.

1. Матрицы и операции над ними.

Правила выполнения линейных операций (сложение, умножение на число) над матрицами, операции транспонирования были рассмотрены в пункте 3.1 теоретической части, операция умножения матриц – в 3.2. Перейдем к решению задач.

Задача 1. Найти матрицу , если

,

Найдем матрицу , транспонированную к, для этого поменяем местами строки и столбцы:.

Найдем матрицу , умножив все элементы матрицына 5:

.

Выполним вычитание матриц и(поэлементно):

.

Задача 2. Найти значение матричного многочлена , если,.

.

Поскольку , то

.

Задача 3. Найти произведение матриц , где

,

Поскольку число столбцов матрицы А совпадает с числом строк матрицы В, то произведение АВ существует: ,.

Следовательно,

.

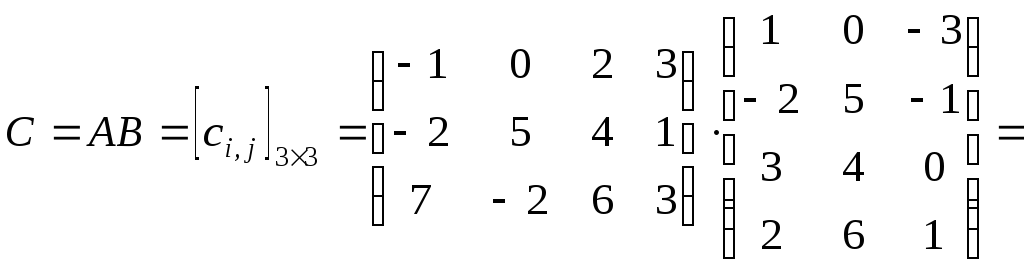
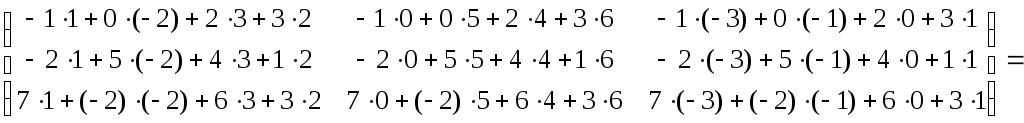
Задача 4. Найти произведение матриц АВ и проверить, коммутируют ли матрицы ,.

Поскольку число столбцов матрицы А совпадает с числом строк матрицы В, то произведение АВ существует. Итак, ,, тогда,

Напомним, что матрицыАВ, для которых АВ=ВА называются коммутирующими. В нашей задаче произведение ВА не существует, так как число столбцов матрицы В не совпадает с числом строк А . А следовательно, матрицыА и В не коммутируют.

1.2. Определители.

Как было показано в пункте 3.3 теоретической части, при вычислении определителей второго порядка используется формула

; при вычислении определителей третьего порядка – «правило треугольников», а также метод разложения определителя по какой-либо строке (столбцу). Отметим, что последним методом можно пользоваться при вычислении определителя произвольного порядка. Вычисляя определитель разложением по строке (столбцу), в качестве строки (столбца), по которой происходит разложение определителя (если в задании не указано иное), выбирают ту строку (столбец), которая содержит больше других нулевых элементов. Если таких столбцов (строк) несколько, то выбирают любую из них.

Задача 5. Вычислить определители:

а) ; б) по «правилу треугольников».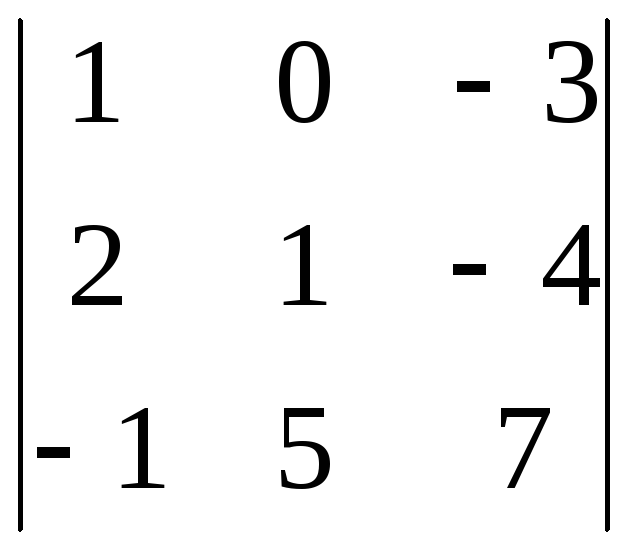

в) разложением по элементам первой строки

г)

а) Поскольку задан определитель второго порядка, то получаем:

.

б) По правилу треугольников, согласно которому три произведения элементов, «относящихся» к главной диагонали, берутся со знаком «+», а три других произведения элементов, «относящихся» к побочной диагонали – со знаком «-», получаем

в) Раскладывая определитель по элементам первой строки, получаем

Определители третьего порядка здесь вычислены по «правилу треугольников».

г) Для вычисления определителя разложим его по третьему столбцу, т.к. именно в этом ряду большее число нулевых элементов:

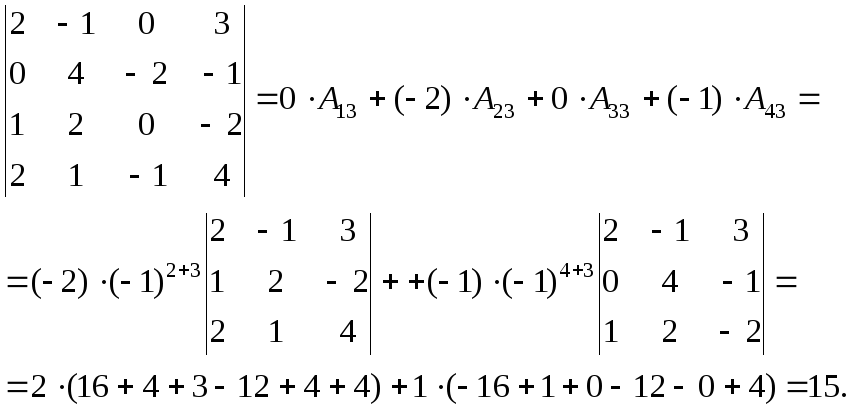
При вычислении определителей, нахождении обратной матрицы, решении систем линейных уравнений и далее при решении задач математического программирования часто используют «правило прямоугольника». Это правило позволяет свести матрицу к треугольному или к диагональному виду, в зависимости от задачи. Определители же треугольных и диагональных матриц равны произведению элементов, стоящих на главной диагонали. Рассмотрим правило прямоугольника на примере вычисления определителей. Алгоритм этого метода приведен в пункте 3.3 теоретической части.

Задача 6. Вычислить .

Шаг 1. В качестве разрешающего элемента выбираем элемент, стоящий на главной диагонали, например, . Тогда строка (первая), в которой он находится, будет разрешающей, а соответствующий столбец (первый)- разрешающим. При записи нового определителя разрешающую строку переписываем, все элементы разрешающего столбца, стоящие ниже, обращаем в ноль; а все элементы, стоящие справа от разрешающего элемента пересчитываем по формуле, где- разрешающий элемент. Получим следующий определитель:

=.

Шаг 2. В качестве разрешающего элемента возьмем .

Первую строку и новую разрешающую строку (вторую) оставляем без изменения, а элементы разрешающего столбца (второго), стоящие под , обращаем в ноль; элементы, стоящие справа от разрешающего элемента пересчитываем по правилу прямоугольника:

=.

Вынесем общий множитель в третьей строки, а в четвертой – множитель, получим:

.

Шаг 3. В качестве разрешающего элемента возьмем элемент .

= =.

Таким образом, исходный определитель равен –72.

Заметим, что с помощью этого метода можно привести определитель и к диагональному виду. В этом случае по правилу прямоугольника пересчитывают все элементы, кроме элементов разрешающей строки.

Приводить определитель к треугольному виду можно и другими элементарными преобразованиями. Покажем это на следующей задаче.

Задача 7. Вычислить определитель приведением к треугольному виду:

.

===

1.3. Обратная матрица.

Обратная матрица существует и единственна тогда и только тогда, когда определитель исходной матрицыА отличен от нуля, т.е. .

В этом случае обратную матрицу находят по формуле (1) из пункта 3.4 теоретической части.

Задача 7. Найти матрицу , обратную к матрице.

Убедимся в том, что матрица А имеет обратную. Для этого вычислим определитель :

Таким образом, поскольку определитель матрицы А отличен от нуля, т.е. матрица А невырожденная, значит, для нее существует обратная матрица.

Для нахождения присоединенной матрицы вычислим алгебраические дополнения элементов матрицыА:

Тогда, согласно формуле

. Значит, .

Проверим правильность вычислений, используя формулу :

Аналогично убеждаемся в том, что .

Таким образом, вычисления обратная матрица найдена верно.

Обратную матрицу можно найти и другим методом – методом элементарных преобразований.

Задача 8. Методом элементарных преобразований найти обратную матрицу к матрице.

Шаг 0. Запишем матрицу, состоящую из исходной матрицы А и единичной матрицы Е такого же размера, что и исходная матрица, т.е. третьего:

.

Цель наших элементарных преобразований – привести матрицу А к единичной.

Шаг 1. Разрешающая строка - , разрешающий столбец -. Применяя правило прямоугольника, преобразуем строки:

.

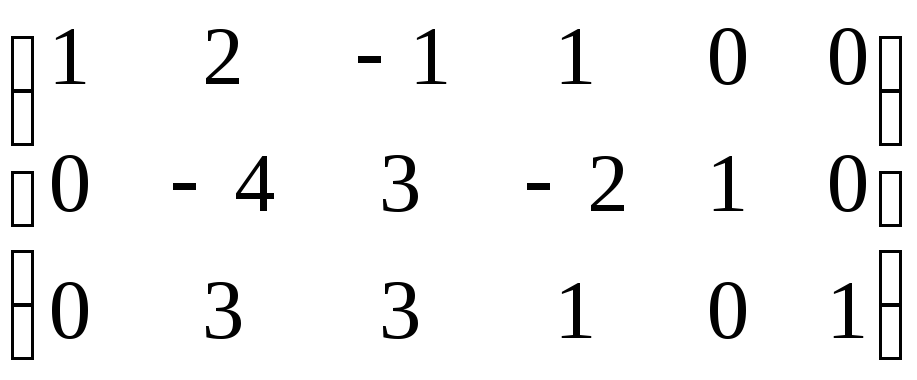
Шаг 2. Разрешающая строка - , разрешающий столбец -. Разделим все элементы разрешающей строки на разрешающий элемент:

.

Применяя правило прямоугольника, преобразуем строки :

.

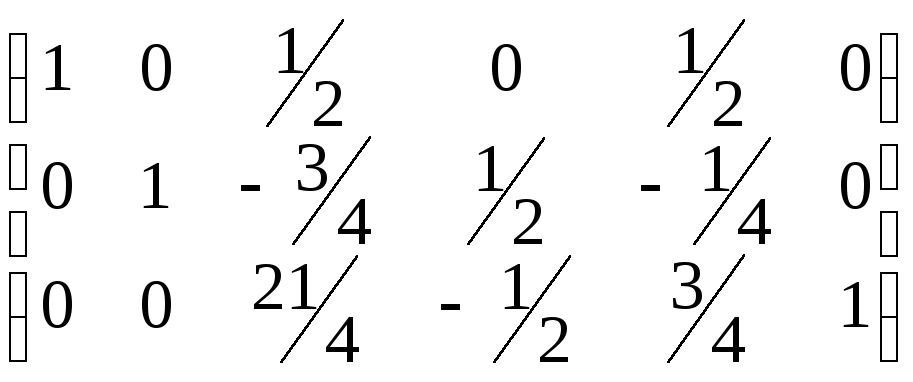
Шаг 3. Разрешающая строка - , разрешающий столбец -. Разделим все элементы разрешающей строки на разрешающий элемент:

.

Применяя правило прямоугольника, преобразуем строки :

.

Поскольку левая половина матрицы – единичная матрица, то преобразования на этом заканчиваются. Правая половина полученной матрицы и есть обратная матрица к исходной, т.е.:

=.

Выполним проверку:

=

=.

Рассмотрим матричные уравнения.

При решении матричных уравнений вида

применяют следующие формулы, соответственно,

, ,.

Задача 9. Решить матричное уравнение

а) ; б).

а) Поскольку , где,то для нахождения матрицыХ сначала вычислим :,

, ,,.

Тогда . Следовательно,.

б) , где,то для нахождения матрицыХ сначала вычислим :,

, ,,.

Тогда. Следовательно,.