Решение
Матрица
имеет размерность 3 3,
то есть является представлением
линейного оператора в пространстве
3,
то есть является представлением
линейного оператора в пространстве .
Собственный вектор матрицы будем искать
в виде:
.
Собственный вектор матрицы будем искать
в виде: .
.
Составим
уравнение для отыскания собственных
векторов в матричном виде:
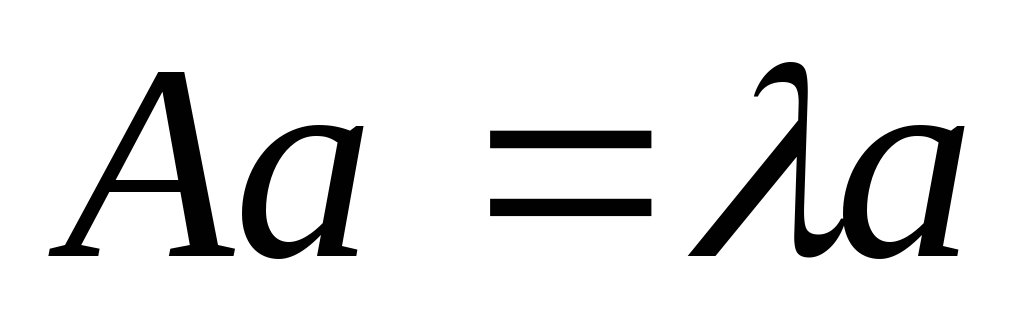




3.
Перепишем матричное уравнение в виде
системы уравнений:

Однородная
система имеет ненулевые решения тогда
и только тогда, когда определитель ее
главной матрицы равен 0. Получаем
характеристическое уравнение системы
и решаем его:

 =
=
=
Корни
уравнения
 находим подбором:
находим подбором: ,
, ,
, 4.
4.
Найдем
собственные векторы для каждого
собственного значения:
|

 ; ;
 ; ;
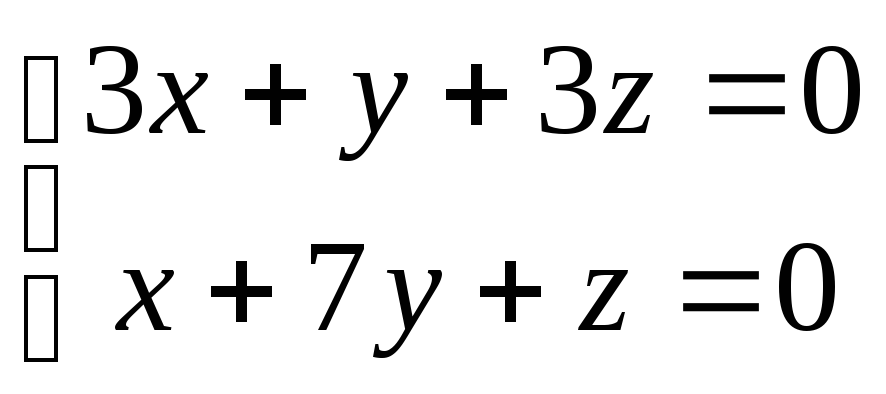 ; ;
 ; ;
 
Пусть
 ,
тогда собственное направление матрицы ,
тогда собственное направление матрицы ,
соответствующее собственному значению ,
соответствующее собственному значению ,
задается множеством векторов: ,
задается множеством векторов:  ,
где ,
где
 . .
|




~  ; ;   . .
Пусть
 ,
тогда собственное направление матрицы ,
тогда собственное направление матрицы ,
соответствующее собственному значению ,
соответствующее собственному значению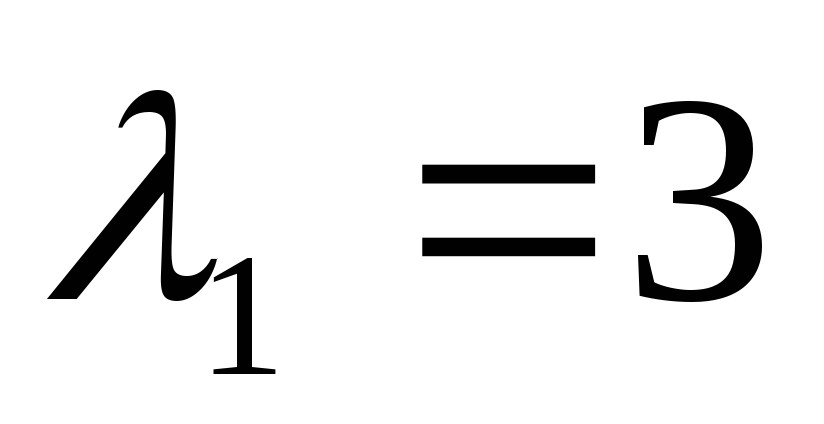 ,
задается множеством векторов: ,
задается множеством векторов:  ,
где ,
где
 . .
|

 ; ;
 ; ;

~  ; ;   . .
Пусть
 ,
тогда собственное направление матрицы ,
тогда собственное направление матрицы ,
соответствующее собственному значению ,
соответствующее собственному значению ,
задается множеством векторов: ,
задается множеством векторов:  ,
где ,
где
 . .
|
Если
выбрать
 =
=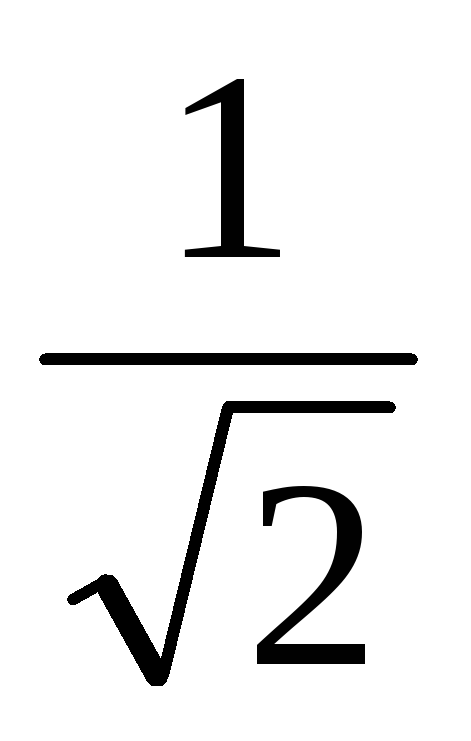 ,
, =
= и
и =
= .
то
.
то ,
, и
и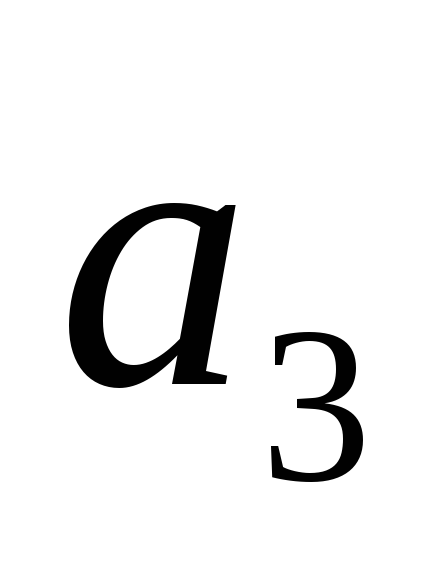 имеют единичную длину:
имеют единичную длину:

 ,
,

 ,
,

 .
.
В
базисе ( )
имеет вид:
)
имеет вид: .
.
Рассмотрим
матрицы перехода от базиса ( )
к базису (
)
к базису ( )
и обратно.
)
и обратно.
Столбцы
матрицы
 =
= - координаты векторов
- координаты векторов в базисе (
в базисе ( ),
следовательно
),
следовательно - матрица перехода от (
- матрица перехода от ( )
к (
)
к ( ).
Найдем матрицу перехода
).
Найдем матрицу перехода от
(
от
( )
к (
)
к ( ):
):
 .
.
Найдем
алгебраические дополнения элементов
матрицы
 :
:
 =
= =
= .
.
Проверка:



 =
= .
.
1Использовано свойство дистрибутивности
умножения матриц относительно сложения: .
.
2Использовано свойство ассоциативности
умножения матриц на число: .
.
3Использовано свойство монотонности
умножения матриц на число: .
.
4Напомним, что для приведенного кубического
уравнения по теореме Виета свободный
член уравнения равен произведению его
корней, взятому с противоположным
знаком. Если уравнение имеет целые
корни, то они являются делителями
свободного члена. Делители числа 36: Подставляя эти числа в уравнение,
находим корни.
Подставляя эти числа в уравнение,
находим корни.
99


 .
.

 ;
; ;
; ,
где
,
где




 ,
где
,
где
 ;
; ;
;

 ,
где
,
где



 .
. =
= - координаты векторов
- координаты векторов =
= =0
=0 =
= =
= =
= =
= =
= =
= =
= =
= .
.
 =
=