1.7. Смешанное произведение векторов

Определение 1.19. Смешанным произведением векторов , и называют число, равное скалярному произведению вектора на векторное произведение векторов и .

(1.8)

Смешанное произведение имеет интересные геометрические приложения. Пусть векторы , и приложены к точке О и представлены

H H’ A B’ C’ D’ B O A’ C D

направленными отрезками , , , . Построим на этих векторах параллелепипед OBDCAB’D’C’. Объем параллелепипеда Vпар равен площади основания SOBDC умноженной на

высоту AA’. Но основание есть параллелограмм, построенный на векторах и , а следовательно его площадь S_OBDC=. перпендикулярен плоскости основания параллелепипеда, а значит, параллелен его высоте AA’. Длина высоты AA’=или .

Итак,

V_пар= AA’ S_OBDC==.

Смешанное произведение ненулевых некомпланарных векторов, образующих правую тройку, равно объему параллелепипеда, построенного на этих векторах:

Если векторы , и образуют левую тройку, то угол между и векторами и тупой, косинус этого угла отрицательный, а значит и скалярное произведение меньше нуля. В этом случае для вычисления объема параллелепипеда следует брать смешанное произведение векторов -, и , образующих правую тройку.

Vпар=, если тройка векторов правая Vпар= - , если тройка векторов левая

(1.9)

Объем треугольной пирамиды (тетраэдра), построенной на трех векторах равен одной шестой их смешанного произведения, взятого со знаком «+», если векторы образуют правую тройку, и со знаком « - «, если левую.

Vтетр=, если тройка векторов правая, Vтетр= - , если тройка векторов левая.

(1.10)

Вывод этих формул основан на известной из школьной программы по геометрии формулы объема тетраэдра: V_тетр=, где - площадь основания пирамиды, и h – ее высота, а также на том факте, что =.

Свойства смешанного произведения:

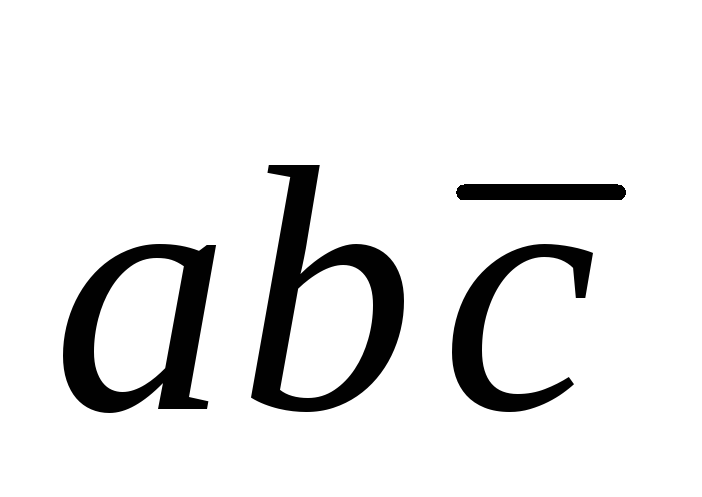1. (а) ==; (б) ==.

Для обоснования этого свойства воспользуемся геометрическим смыслом смешанного произведения. Из рис. 1.20 (а,б) видно, что если тройка является правой, то правыми являются также тройки и , а тройки , , являются левыми. Смешанные произведения векторов , и в любом порядке, представляют объем одного и того же параллелепипеда, взятый со знаком «+» для правых троек, и со знаком « – « для левых. Это и является подтверждением указанных равенств. Кроме того, любое смешанное произведение из группы (а) равно любому смешанному произведению из группы (б), взятому со знаком «- «.

2. Если , то =0 тогда и только тогда, когда , и компланарны.