1.6. Векторное произведение векторов

Напомним, что базис векторного пространства V³ - это упорядоченная тройка некомпланарных векторов. Рассмотрим, чем, с геометрической точки зрения, различаются тройки, состоящие из одних и тех же векторов, но по-разному упорядоченные. Векторы могут быть упорядочены следующими способами:

, , , , , .

Рис. 1.20 (а). Правые тройки векторов			1.20 (б). Левые тройки векторов

Определение 1.17. Тройку некомпланарных векторов называют правой тройкой векторов, если, глядя из конца первого вектора на второй и третий, движение от второго к третьему происходит справа налево (против часовой стрелки), и левой тройкой векторов, - если слева направо (по часовой стрелке).

На рис. 1.20 (а,б) показаны правые и левые тройки векторов , и .

Понятие векторного произведения связывает длины и направления векторов множителей , и порядок их следования в парах (,) и (,).

Определение 1.18. Векторным произведением векторов и называют вектор , такой, что: если и коллинеарны, то , если же и неколлинеарны, то:

1. ,

2. перпендикулярен плоскости, в которой лежат векторы и , то есть перпендикулярен как вектору , так и вектору,

3. тройка векторов 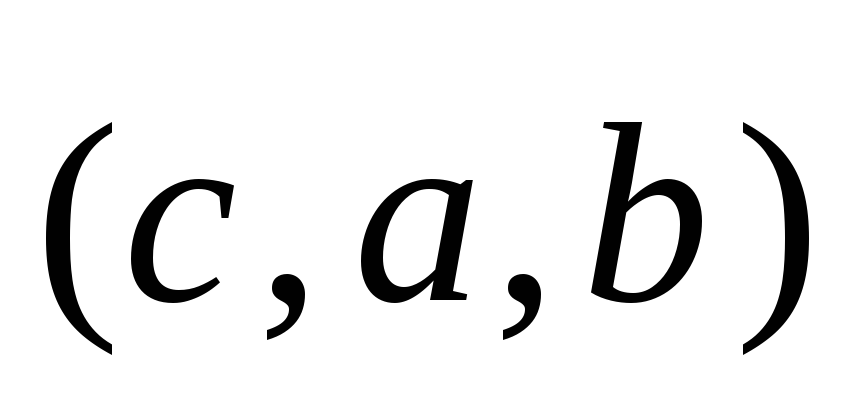- правая.

Напомним, что величина угла положительна, если движение от к происходит против часовой стрелки, и отрицательна, - если по часовой стрелке, а также: . В определении модуля векторного произведения использован . Очевидно, , следовательно, и . Если знак модуля величины угла опустить, то может оказаться отрицательным, а это невозможно.На рис. 1.21 показаны векторные произведения и . Оба они перпендикулярны плоскости P, одинаковы по длине, но противонаправлены . Следовательно, = - : векторное произведение антикоммутативно.

Перечислим свойства векторного произведения:

O

Рис. 1.21. Векторные произведения и

1. Антикоммутативность: = - .

2. Дистрибутивность относительно сложения векторов: .

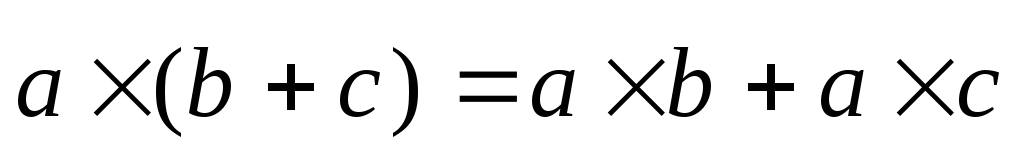3. Однородность: .

С помощью векторного произведения решают следующие геометрические задачи:

1. Установление кооллинеарности ненулевых векторов:

коллинеарен .

2. Вычисление площадей треугольника и параллелограмма. Отметим, что согласно формулам школьного курса геометрии, = =S_пар =2S_ , где S_пар- площадь параллелограмма., а S_ - площадь треугольника, построенных на векторах и .

Справедливо следующее утверждение: если тройка ненулевых векторов правая, то угол острый, если левая, - то тупой. Поясним данное утверждение чертежом. Пусть векторы и лежат в плоскости Р.

O P -

Вектор перпендикулярен плоскости Р и тройка векторов () правая. Назовем условно часть пространства, где лежит конец вектора : «сверху от плоскости Р». Все векторы, образующие с (, ) правую тройку и приложенные к точке О, также

заканчиваются сверху от плоскости Р, а те, которые образуют левую тройку – снизу от этой плоскости. Но все векторы, приложенные к точке О , конец которых лежит сверху от плоскости Р, образуют с вектором острый угол, те же, конец которых лежит снизу от нее, образуют острый угол с вектором -, а следовательно с вектором угол будет тупым. Из чертежа также видно, что если вектор образует с (, ) правую тройку, то (-) – левую.