
- •Математика
- •Оглавление
- •1. Пространство геометрических векторов
- •Геометрический вектор. Длина и направление вектора. Равенство векторов
- •1.2. Линейные операции над векторами
- •1.3. Свойства линейных операций над геометрическими векторами
- •1.4. Линейная зависимость и линейная независимость систем
- •Доказательство
- •1.5. Скалярное произведение векторов
- •Решение
- •1.6. Векторное произведение векторов
- •1.7. Смешанное произведение векторов
- •2. Система координат. Арифметические векторы
- •2.1. Декартова прямоугольная система координат. Координаты вектора
- •2.2. Операции над арифметическими векторами
- •2.3. Линейные векторные пространства. Базис линейного пространства
- •3. Матрицы и определители
- •3.1. Матрицы, их классификация и линейные операции над ними
- •Равенство матриц
- •Умножение матрицы на число
- •Сложение матриц
- •3.2. Умножение матриц
- •Свойства умножения матриц
- •3.3. Определители. Общие методы их вычисления
- •1. Вычисление определителей второго порядка.
- •2. Вычисление определителей третьего порядка
- •3. Вычисление определителя порядка n
- •3.4. Свойства определителей. Методы вычисления, основанные на свойствах
- •3.5. Нахождение обратной матрицы
- •3.6. Ранг матрицы
- •4. Системы линейных алгебраических уравнений
- •4.1. Основные понятия и определения
- •4.2. Решение систем с квадратной матрицей
- •4.3. Решение слау методом Гаусса
- •Решение
- •4.4. Однородные слау и их решение
- •4.5. Обобщение теории слау
1.5. Скалярное произведение векторов
Скалярное произведение связывает воедино длины векторов и величины углов между ними.
Определение
1.16. Скалярным
произведением векторов
![]() и
и
![]() называют
число,
равное произведению длин этих векторов
на косинус угла между ними, если
называют
число,
равное произведению длин этих векторов
на косинус угла между ними, если
![]() ,
,
![]() ,
и равное нулю, если хотя бы один из
векторов нулевой.
,
и равное нулю, если хотя бы один из
векторов нулевой.
|
|
(1.1) |
|
O
Рис.
1.18. Угол между векторами |
Величину
угла
Для
векторов на рис. 1.18:
Будем
считать, что для любых векторов |
Основные свойства скалярного умножения векторов:
1.
Коммутативность:
![]() .
.
2.
Дистрибутивность относительно сложения
векторов:
![]() .
.
3.
Однородность:
![]() .
.
4.
Свойство скалярного квадрата:
![]() .
.
Свойства 1 и 4 очевидны, свойства 2 и 3 можно проиллюстрировать чертежом. Выполните это самостоятельно для пространств V2 и V3.
С помощью скалярного произведения решают следующие задачи:
1. Нахождение длины вектора, представленного линейной комбинацией известных векторов.
2. Установление ортогональности векторов.
3. Нахождение угла между векторами по известному скалярному произведению и длинам векторов.
Пример.
|
P A
M
B O
C |
Дано:
Найти: (1)
|
Решение

 =(
=( )2=9
)2=9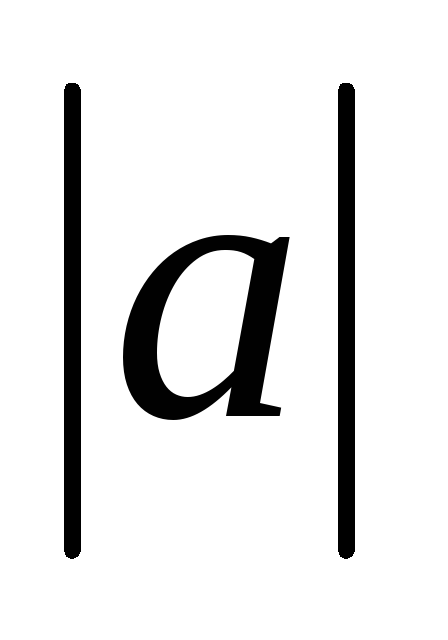 2-3
2-3
 +
+ =94-34.5+
=94-34.5+ =27.5625,
=27.5625,
 .
. COM,
COM,
 COM=
COM= .
.
![]()
![]() ,
,
![]()
![]() .
.
![]() COM=
COM=![]() ,
COM.
,
COM.![]() .
.
С понятие скалярного произведения тесно связано понятие проекции вектора на вектор, вектора на ось, вектора на плоскость которые определяются следующими формулами:
|
проекция
вектора
|
(1.2) |
|
проекция
вектора
|
(1.3) |
|
проекция
вектора
|
(1.4) |
Рис 1.19 (а,б) иллюстрирует эти понятия.
Сравнивая формулы (1.1) и (1.2), легко видеть, что
|
|
(1.5) |
|
B A
B’ O S A’ x
|
A
O A’’ x
|
|
Рис.1.19
(а). Проекции векторов
|
Рис.1.19
(б). Проекции вектора
|
Формулу
(1.5) перепишем следующим образом: ![]() =
=![]() .
Очевидно, что вектор
.
Очевидно, что вектор ![]() имеет длину, равную 1, и сонаправлен
имеет длину, равную 1, и сонаправлен ![]() .
Такой вектор называют ортом
вектора
.
Такой вектор называют ортом
вектора ![]() и обозначают:
и обозначают:![]() .
Используя понятие орта, проекцию вектора
на вектор можно записать следующей
формулой:
.
Используя понятие орта, проекцию вектора
на вектор можно записать следующей
формулой:
|
|
(1.6) |
Для проекции вектора на ось справедлива следующая формула:
|
|
(1.7) |
где
![]() - единичный вектор оси.
- единичный вектор оси.
Из формулы (1.6) и свойств скалярного произведения вытекают свойства проекций:
 или
или
 перпендикулярен
перпендикулярен
 .
. .
Если вектор умножить на какое-либо
число, то и проекция его будет умножена
на это же число.
.
Если вектор умножить на какое-либо
число, то и проекция его будет умножена
на это же число. .
Проекция суммы векторов равна сумме
проекций этих векторов.
.
Проекция суммы векторов равна сумме
проекций этих векторов.





