Доказательство

Необходимость. Пусть невырожденной линейно комбинации векторов системы не существует. Это означает, что лишь в том случае, когда все числовые коэффициенты нули, линейная комбинация равна нуль-вектору: . Но из такой линейной комбинации ни один вектор нельзя выразить через другие векторы, так как деление на нуль невозможно. Это значит, что данная система векторов является свободной.

Достаточность. Пусть существует невырожденная нулевая линейная комбинация векторов системы: , причем хотя бы один из числовых коэффициентов отличен от нуля. Пусть . Тогда . Это означает, что вектор представим линейной комбинацией остальных векторов системы. Тогда по определению 1.13, система является несвободной.

Справедливы следующие утверждения:

Утверждение 1. Система векторов, содержащая нуль-вектор, несвободна.

Утверждение 2. Система векторов, содержащая коллинеарные векторы, несвободна.

Утверждение 3. Система векторов пространства V² , содержащая более двух векторов, несвободна.

Утверждение 4. Система векторов пространства V³ , содержащая более трех векторов, несвободна.

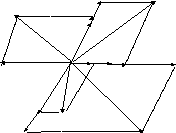
Справедливость утверждений 1 и 2 очевидна. Утверждения 3 и 4 означают, что в пространстве компланарных векторов любой вектор можно представить линейной комбинацией двух неколлинеарных векторов, а в пространстве V³ – линейной комбинацией трех некомпланарных векторов. Каким образом это можно сделать, показано на рис. 1.15 и 1.16.

Определение 1.14. Систему векторов называют максимальной линейно независимой системой векторов векторного пространства, если она свободна, но добавление к ней еще одного вектора этого же пространства делает ее линейно зависимой.

Определение 1.15. Базисом векторного пространства называют максимальную систему линейно независимых векторов этого пространства.

Пусть - какой-либо ненулевой вектор пространства V¹ . Как отмечено в разделе 1.2 любой вектор этого пространства, а также все векторы, коллинеарные ему, можно представить в виде: = (). Такое представление называют разложением вектора по базису (), число x - координатой вектора в данном базисе.

Пусть - система неколлинеарных векторов пространства V² . На рис. 1.15 показано, как любой вектор этого пространства можно представить в виде линейной комбинации векторов : .

Как видно из рис.1.15, вектор есть сумма векторов и , так как является диагональю параллелограмма, построенного на этих векторах.

= О = = Рис.1.15. Разложение компланарных векторов , ,, по базису (, )

Так как базисные векторы , неколлинеарны и , , всегда найдутся числа такие, что на векторах , можно построить параллелограмм, диагональю которого является вектор . Аналогичные рассуждения можно провести и обо всех остальных векторах. Представление . называют разложением вектора по базису (, ), числа x,y - координатами вектора в данном базисе.

Вектор, некомпланарный векторам , представить в виде линейной комбинации этих векторов невозможно, так как любая их линейная комбинация им компланарна. Пусть - система некомпланарных векторов пространства V³ . На рис. 1.16 показано, как любой вектор этого пространства можно представить в виде: . Такое представление называют разложением вектора по базису (,,), Числа x,y,z - координатами вектора в данном базисе.

= O

Рис 1.16 Разложение вектора по базису

Базисом пространства V¹ может служить любой ненулевой вектор этого пространства. Базисом пространства V² может служить любая пара неколлинеарных векторов этого пространства. Базисом пространства V³ может служить любая тройка некомпланарных векторов этого пространства. Базис выбирается из соображений удобства в каждой конкретной задаче. Если базис выбран, все остальные векторы пространства единственным образом представляются в виде линейных комбинаций базисных векторов, то есть раскладываются по выбранному базису. Координаты вектора при выбранном базисе определяются единственным образом.

В большинстве практически важных задач выбирают ортонормированные базисы. Такие базисы состоят из векторов единичной длины (нормированных векторов) перпендикулярных (ортогональных) друг другу (.рис.1.17 а,б,в). Базисные векторы ортонормированных базисов принято обозначать: ,,.

Рис. 1.17(a) Нормированный базис пространства V1

Рис. 1.17(б) Ортонормированный базис пространства V2

Рис. 1.17(в) Ортонормированный базис пространства V3