1.3. Свойства линейных операций над геометрическими векторами

Приведенные ниже свойства линейных операций над геометрическими векторами либо очевидны, либо легко проверяются с помощью построений.

1. Ассоциативность сложения: .²

2. Коммутативность сложения: .

3. Свойство нуль-вектора: 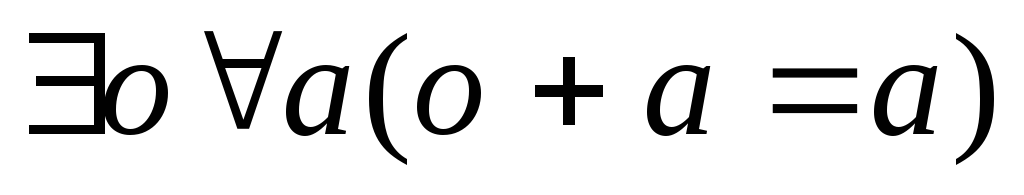.³

4. Наличие противоположного вектора: .

5. Смешанная ассоциативность: .⁴

6. Дистрибутивность умножения относительно сложения векторов:

.

7. Дистрибутивность умножения относительно сложения чисел:

.

8. Свойство единицы: ).

Проиллюстрируем для примера справедливость свойства 6. Возьмем произвольные векторы ии числоx (пусть x>0). Векторы xиxколлинеарны векторами. Приложим векторыиxк точке A, представив их направленными отрезками и, лежащими на одной

x B` B A C C`

прямой. Приложив вектор xк точкеB’, представив его направленным отрезком . Тогда: (*) Из точки B проведем отрезок BC, параллельный B’C’, до пересечения с отрезком AC’ И зададим ему направление так, чтобы. По правилу треугольника:

.

Треугольники ABC и A’B’C’ подобны как треугольники с параллельными сторонами, а значит стороны их пропорциональны:

.

Отсюда:

.

Следовательно:

Из равенств (1) и (2) получаем:

,

что и требовалось доказать.

1.4. Линейная зависимость и линейная независимость систем

геометрических векторов. Базис векторного пространства

Определение 1.10. Системой векторов называют последовательность векторов .

Подчеркнем, что в системе векторов важен порядок следования векторов друг за другом. Например, системы и не равны: хотя они состоят из одних и тех же векторов, но порядок следования векторов в них различен.

Определение 1.11. Линейной комбинацией векторов называют вектор вида: , где .

Очевидно, что если все числовые коэффициенты в линейной комбинации равны нулю, то и вся линейная комбинация равна нуль-вектору. Обратное утверждение верно не всегда: существуют линейные комбинации с ненулевыми коэффициентами, равные нуль-вектору. Например, для системы векторов () на рис. 1.15 линейная комбинация +, поскольку +, несмотря на то, что все ее числовые коэффициенты () отличны от нуля.

Определение 1.12. Нулевой линейной комбинацией системы векторов называют линейную комбинацию равную нуль-вектору. Вырожденной линейной комбинацией системы векторов называют линейную комбинацию, все числовые коэффициенты которой равны нулю.

В этих терминах приведенное выше рассуждение можно записать так:

всякая вырожденная линейная комбинация является нулевой, но существуют нулевые комбинации не являющиеся вырожденными.

Определение 1.13. Линейно независимой или свободной системой векторов векторного пространства называют систему векторов , если ни один из векторов системы не представим линейной комбинацией остальных векторов. Если хотя бы один из векторов системы можно представить линейной комбинацией остальных векторов, система называется линейно зависимой или несвободной.

Теорема 1. Для того, чтобы система векторов была линейно зависима, необходимо и достаточно, чтобы существовала невырожденная нулевая комбинация векторов системы.