1.2. Линейные операции над векторами

Линейные операции над векторами – это умножение вектора на число, сложение и вычитание векторов. Все векторы будем рассматривать в пространствах V₁, V₂ или V₃ .

Определение 1.7. Произведением вектора на число x () называют вектор , длина которого равна, а направление совпадает с направлением, еслиx положительно, и противоположно вектору , еслиx – отрицательно. Если , то=.

Кратко определение 1.7 можно записать так:

=;

1. длина :=,

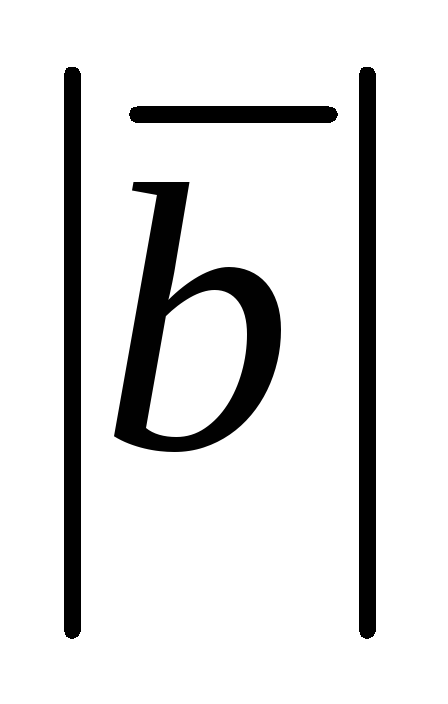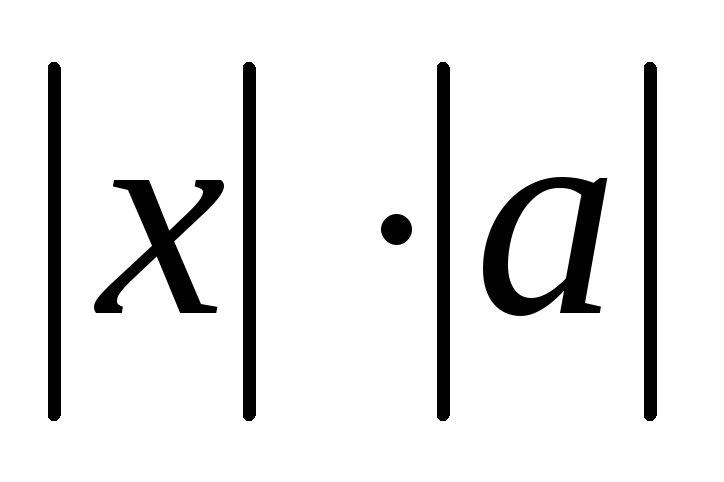2. направление :.

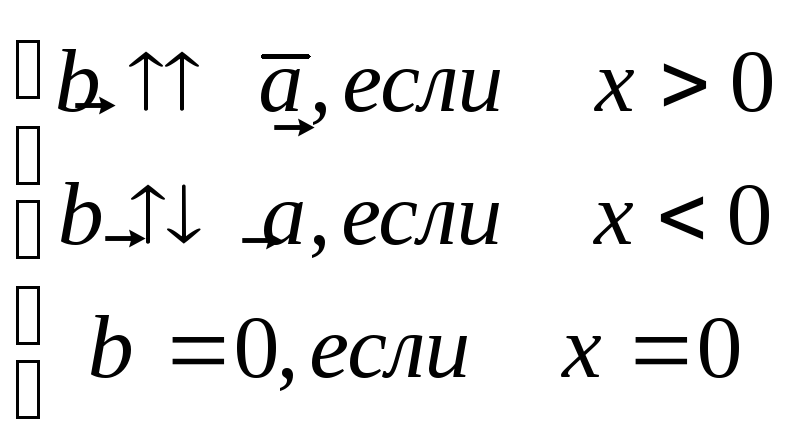На рис. 1.7 показано, как практически строят вектор =для различныхx.

B A O  C

Рис. 1.7. Умножение вектора на число: ,

Если постулировать коллинеарность нуль-вектора любому другому вектору, то будет справеливо следующее очевидное утверждение:

Утв.1 Вектор коллинеарен, каково бы ни было число x.

Из утв.1 следует, что множество всех коллинеарных друг другу векторовV¹ – это множество всех векторов, вида , где- базисный вектор, а- переменная, значениями которой являются действительные числа ().

Очевидно, что умножив вектор на (-1), получим противоположный ему вектор. Вектор противоположный вектору будем обозначать «-».

Определение 1.8. Суммой векторов иназывают вектор , начало которого совпадает с началом вектора , а конец – с концом вектора , при условии, что начало вектора совпадает с концом вектора . В определении 1.8 описано известное из школьного курса геометрии правило треугольника для сложения векторов. Его иллюстрирует рис.1.8 и 1.9.

= A B C A C B = Рис. 1.8. Сложение коллинеарных векторов

Рис. 1.9. Правило треугольника сложения векторов

Рис. 1.10. правило параллелограмма сложения векторов

C O B A Рис.1.11. Сложение трех векторов по правилу параллелограмма

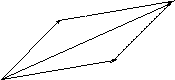
Кроме правила треугольника, для сложения векторов используется правило параллелограмма, иллюстрируемое рис. 1.10 и 1.11: если векторы иприложены к одной точке, то их суммаесть вектор, начало которого приложено к той же точке, а конец – совпадает с противолежащей вершиной параллелограмма, построенного на векторахи.

Подчеркнем, что сумма коллинеарные векторов есть вектор, коллинеарный слагаемым (рис.1.8), умножая на числа и складывая компланарные векторы, получаем вектор, компланарный слагаемым (.рис.1.9, рис.1.10). Умножая на числа и складывая векторы пространства V³, получаем вектор пространства V³ (рис.1.11). Таким образом, каждое из векторных пространств V¹, V² и V³ замкнуто отностиельно операций умножения вектора на число и сложения векторов.

Определение 1.9. Разностью векторов иназывают вектор , равный сумме вектора и вектора, противоположного вектору .

На рис.1.12-1.14 показаны правила выполнения вычитания векторов.

-- - -	- --	- -
Рис.1.12. Вычитание коллинеарных векторов	Рис. 1.13. Вычитание векторов по правилу параллелограмма	Рис. 1.14. Вычитание векторов по правилу треугольника.