
- •Математика
- •Оглавление
- •1. Пространство геометрических векторов
- •Геометрический вектор. Длина и направление вектора. Равенство векторов
- •1.2. Линейные операции над векторами
- •1.3. Свойства линейных операций над геометрическими векторами
- •1.4. Линейная зависимость и линейная независимость систем
- •Доказательство
- •1.5. Скалярное произведение векторов
- •Решение
- •1.6. Векторное произведение векторов
- •1.7. Смешанное произведение векторов
- •2. Система координат. Арифметические векторы
- •2.1. Декартова прямоугольная система координат. Координаты вектора
- •2.2. Операции над арифметическими векторами
- •2.3. Линейные векторные пространства. Базис линейного пространства
- •3. Матрицы и определители
- •3.1. Матрицы, их классификация и линейные операции над ними
- •Равенство матриц
- •Умножение матрицы на число
- •Сложение матриц
- •3.2. Умножение матриц
- •Свойства умножения матриц
- •3.3. Определители. Общие методы их вычисления
- •1. Вычисление определителей второго порядка.
- •2. Вычисление определителей третьего порядка
- •3. Вычисление определителя порядка n
- •3.4. Свойства определителей. Методы вычисления, основанные на свойствах
- •3.5. Нахождение обратной матрицы
- •3.6. Ранг матрицы
- •4. Системы линейных алгебраических уравнений
- •4.1. Основные понятия и определения
- •4.2. Решение систем с квадратной матрицей
- •4.3. Решение слау методом Гаусса
- •Решение
- •4.4. Однородные слау и их решение
- •4.5. Обобщение теории слау
4.4. Однородные слау и их решение
Определение 4.4. СЛАУ называют однородной системой, если ее столбец свободных членов состоит из нулей:
|
|
(4.5) |
где
 .
.
В разделе 2.3 (формула 2.23), было отмечено, что решение вопроса о линейной зависимости и линейной независимости системы векторов, сводится к решению однородной СЛАУ: На основании Теоремы 1, вопрос о линейной зависимости или линейной независимости системы n-мерных арифметических векторов может быть решен с помощью системы уравнений:
|
|
(2.23) |
Таким
образом, вопрос о линейной зависимости
и линейной независимости системы
векторов, сводится к вопросу о решении
однородной системы уравнений: если
(2.23) имеет только нулевое решение, то
система векторов (![]() )
свободна, если же имеются ненулевые
решения, то система векторов линейно
зависима.
)
свободна, если же имеются ненулевые
решения, то система векторов линейно
зависима.
Дадим ответ на вопрос, в каких случаях однородная СЛАУ (4.5) имеет единственное нулевое решение, а в каких бесконечно много решений..
Выпишем расширенную матрицу системы (4.5):
![]() .
.
Поскольку
столбец свободных членов нулевой, то
ранг расширенной матрицы не может быть
выше ранга главной матрицы. Поэтому
система (4.5) всегда совместна. Напомним
(см. раздел 4.3), что, если
![]() ,
то совместная система имеет единственное
решение, если же
,
то совместная система имеет единственное
решение, если же![]() ,
то решений бесконечно много. Поэтому,
если число переменных однородной СЛАУ
равно рангу матрицы системы, то система
имеет единственное решение – это нулевое
решение.
,
то решений бесконечно много. Поэтому,
если число переменных однородной СЛАУ
равно рангу матрицы системы, то система
имеет единственное решение – это нулевое
решение.
Таким образом, если после преобразований матрицы однородной СЛАУ, матрица приведена к квадратной матрице, то векторы - столбцы этой матрицы образуют линейно независимую систему.
Если
![]() ,
то для нахождениявсех
решений СЛАУ
(4.5) выполним последовательность операций:
,
то для нахождениявсех
решений СЛАУ
(4.5) выполним последовательность операций:
Выполнить элементарные преобразования строк матрицы
 и перестановку ее столбцов. В результате
этих преобразований установить
эквивалентность матрицы
и перестановку ее столбцов. В результате
этих преобразований установить
эквивалентность матрицы матрице вида
матрице вида :
: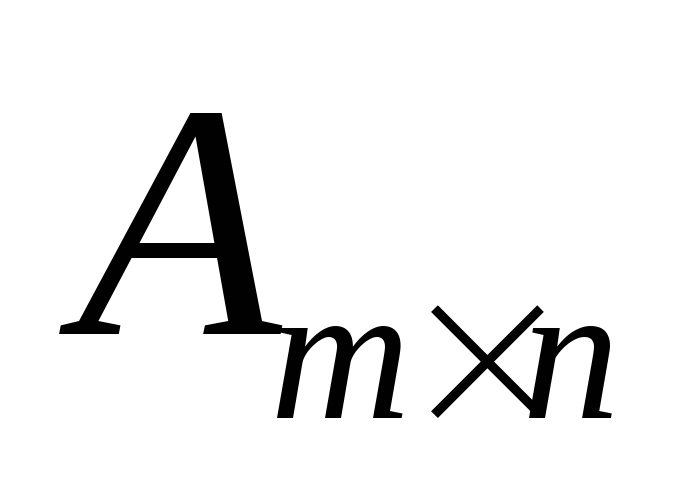 ~
~
Объявить неизвестные, соответствующие матрице
 ,
базисными переменными; неизвестные,
соответствующие матрице
,
базисными переменными; неизвестные,
соответствующие матрице - свободными переменными.
- свободными переменными.Придавая свободным переменным произвольные значения
 и,
выражая через них базисные переменные,
получить общее решение однородной
СЛАУ.
и,
выражая через них базисные переменные,
получить общее решение однородной
СЛАУ.
Рассмотрим пример решения однородной системы.
Пример.
Решить
систему:
 .
.
Решение.
 ~
~
 ~ ~
~ ~![]()
 ~
~![]()
![]() ~
~
~![]()
![]() ~
~![]()
![]() .
.
Базисные
переменные: (![]() ),
свободные переменные: (
),
свободные переменные: (![]() ).
).
Пусть
![]() ,
где
,
где![]() - произвольные константы (любые
действительные числа). Тогда:
- произвольные константы (любые
действительные числа). Тогда:![]() ,
,![]()
Запишем решение в векторном виде:
![]() =
= =C1
=C1 +C2
+C2 +C3
+C3![]() .
.
Проанализируем полученное решение. В записи решения участвуют три вектора
![]() =
=
 ,
,![]() =
= ,
,![]() =
=![]() .
.
Первые
две координаты этих векторов соответствуют
базисным переменным
![]() ,
последние три – свободным переменным
,
последние три – свободным переменным![]() .
В каждом из векторов одна из свободных
переменных принимает значение 1, а
остальные две – 0. Такую систему векторов
называютфундаментальной
системой решений однородной СЛАУ.
Общее решение СЛАУ есть сумма произведений
векторов фундаментальной системы на
произвольные константы
.
В каждом из векторов одна из свободных
переменных принимает значение 1, а
остальные две – 0. Такую систему векторов
называютфундаментальной
системой решений однородной СЛАУ.
Общее решение СЛАУ есть сумма произведений
векторов фундаментальной системы на
произвольные константы
![]() .
.
Итак,
общее решение однородной СЛАУ
![]() ,
при условии
,
при условии![]() может быть представлено следующим
образом:
может быть представлено следующим
образом:
![]() ,
,
где
![]() произвольные действительные числа,
(
произвольные действительные числа,
(![]() )
фундаментальная система решений, первыеr
компонентов которых соответствуют
базисным переменным, последние (n-r)
– свободным переменным, причем в каждом
векторе
)
фундаментальная система решений, первыеr
компонентов которых соответствуют
базисным переменным, последние (n-r)
– свободным переменным, причем в каждом
векторе
![]() свободная переменная
свободная переменная![]() принимает
значение 1, а все остальные свободные
переменные – значения 0.
принимает
значение 1, а все остальные свободные
переменные – значения 0.
Назначение
одних переменных базисными, а других –
свободными, определяется смысловым
значением этих переменных. В связи с
этим, возникает задача о переводе
свободных переменных в базисные, а
базисных - в свободные. Пусть, например,
требуется перевести
свободные переменную
![]() в базис, а базисную переменную
в базис, а базисную переменную![]() сделать свободной:
сделать свободной:
![]() ~
~![]()
![]() ~
~
~![]()
![]() ~
~![]()
![]()
Базисные
переменные: (![]() ),
свободные переменные: (
),
свободные переменные: (![]() ).
).
Пусть
![]() ,
где
,
где![]() - произвольные константы. Тогда:
- произвольные константы. Тогда:![]() ,
,![]()
Запишем решение в векторном виде:
![]() =
= =
=
=C1 +C2
+C2 +C3
+C3![]() =
=
![]() .
.
Отметим, что кратко общее решение однородной системы можно записать в виде:
![]() ,
,
где
![]() - столбец неизвестных,
- столбец неизвестных,![]() - строка произвольных констант,
- строка произвольных констант,![]() - матрица размерности
- матрица размерности![]() ,
столбцами которой являются фундаментальные
решения однородной системы.
,
столбцами которой являются фундаментальные
решения однородной системы.

