4.3. Решение слау методом Гаусса

Метод или алгоритм Гаусса позволяет решить любую СЛАУ. В школьном курсе данный алгоритм называют методом последовательного исключения переменных. Приведем пример «школьного» решения системы.

Пример.

Решить систему: .

Решение.

Поменяем местами первое и второе уравнения: ;

Вычтем из второго уравнения удвоенное первое, а к третьему прибавим первое: ; (из второго и третьего уравнений исключена переменнаяx).

Разделим второе уравнение на (-7): ;

Вычтем из третьего уравнения второе:

; (из третьего уравнения исключены переменные x и y).

Получаем: .

Каждый шаг этого алгоритма опирается на свойства числовых равенств и переводит СЛАУ в равносильную ей СЛАУ. Решение последней системы очевидно, но оно же является и решением исходной системы по причине их равносильности.

Если выполнять аналогичные преобразования не над самими уравнениями, а над строками расширенной матрицы системы, то это будут элементарные преобразования строк матрицы, причем каждая преобразованная матрица есть матрица системы, которая равносильна исходной.

Рассмотрим решение трех систем, выполняя элементарные преобразования над строками их расширенных матриц.

Пример1. Решить систему: .

Решение.

Запишем расширенную матрицу системы:

.

Выполним элементарные преобразования над строками расширенной матрицы:

~~~

~~~~

~

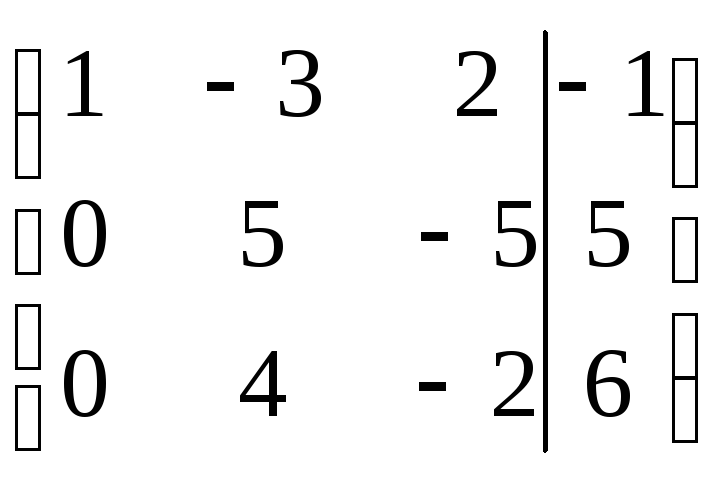Обратим внимание на то, что

• ранг главной матрицы системы равен рангу расширенной матрицы системы,

• число неизвестных равно рангу матрицы,

• система имеет единственное решение: .

Пример 2. Решить систему: .

Решение

~~~

.

Последняя матрица – это матрица системы:

.

Так как равенство 0 = -1 ложно при любых значениях переменных x₁ , x₂ , x₃ , то система несовместна.

Очевидно, что в матрице ранг главной матрицы равен 2, ранг расширенной матрицы равен 3. Элементарные преобразования не меняют рангов главной и расширенной матриц системы. Поэтому:если ранг главной матрицы системы меньше ранга расширенной матрицы системы, то система не имеет решения.

Пример 3.

Решение

~~~

~~.

Главная матрица системы в данном примере имеет вид: . Единичной матрицесоответствуют переменные. Назовем ихбазисными переменными. Матрице H соответствует переменная . Назовем еесвободной переменной.

В данном примере ранг главной матрицы равен рангу расширенной матрицы (равен 2), но число неизвестных больше ранга главной и расширенной матриц. Преобразованная матрица соответствует системе:

.

Последнее равенство системы справедливо при любых значениях неизвестных. Придадим свободной переменной произвольное значение: , где- любое действительное число. Тогда решение системы имеет вид:. При любом значенииC числа удовлетворяют всем уравнениям системы. Очевидно, что в данном примере система имеет не единственное решение, а множество решений, различающихся между собой значениямипроизвольной постоянной C. Такое множество решений называют общим решением системы. Придавая произвольной постоянной конкретное значение, получаем частное решение системы. Запишем общее решение в виде вектора столбца:

+=+.

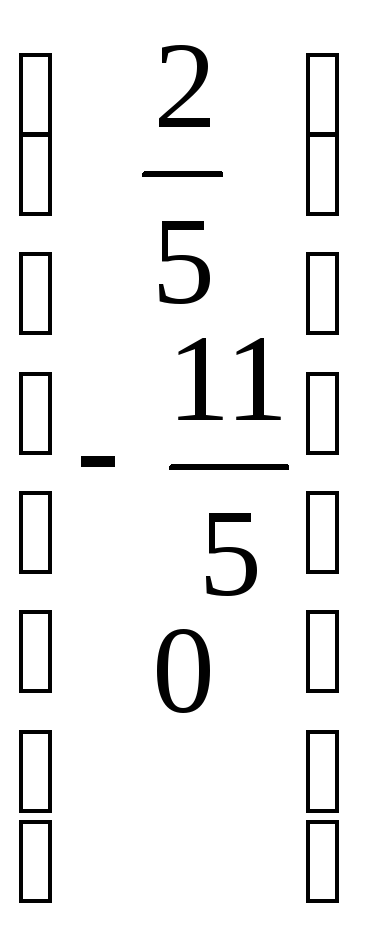В последней записи вектор столбец решений разбит на сумму постоянного вектора, в котором свободная переменная = 0, и множество коллинеарных друг другу векторов: .

Таким образом, если ранг главной матрицы системы равен рангу ее расширенной матрицы, а число переменных больше ранга этих матриц, то система имеет бесконечно много решений.

Обобщим выводы, сделанные по каждому из примеров.

Выводы.

Пусть дана СЛАУ: изm уравнений, содержащая n неизвестных. Чтобы решить систему, выполняем элементарные преобразования строк расширенной матрицы системы и перестановку столбцов главной матрицы. В результате этих преобразований устанавливается эквивалентность расширенной матрицы системы матрице одного из следующих видов, причем каждый из видов полностью определяет решение системы:

1. ~, ранг главной матрицыr меньше ранга расширенной матрицы r+1. Система несовместна (не имеет решений).

2. ~, ранг главной матрицы равен рангу расширенной матрицы и равен числу неизвестных системы. Система имеет единственное решение, которое с точностью до нумерации неизвестных имеет вид:, где- элементы столбца.

3. ~, ранг главной матрицы равен рангу расширенной матрицы, но меньше числа неизвестных (r<n). При этом ~, где,- единичная матрица порядкаr. Система имеет множество решений. Это множество решений находим в следующем порядке:

3.1. Объявляем неизвестные, соответствующие матрице , базисными переменными; переменные, соответствующие матрице- свободными переменными.

3.2. Придавая свободным переменным произвольные значения и, выражая через них базисные переменные, получаем общее решение СЛАУ.