4. Системы линейных алгебраических уравнений

4.1. Основные понятия и определения

Определение 1. Систему равенств вида:

(4.1)

где =числовая матрица,- вектор столбец чисел,- вектор столбец переменных, называютсистемой m линейных алгебраических уравнений c n неизвестными (СЛАУ).

Кратко СЛАУ можно записать в виде матричного равенства:

(4.2)

Матрицуназываютглавной матрицей системы (4.1), матрицу -расширенной матрицей системы, столбец -столбцом неизвестных, столбец -столбцом свободных членов.

В школьном курсе математики изучаются простейшие СЛАУ, в которых число уравнений не превышает трех и равно числу неизвестных. Однако в экономических дисциплинах, применяющих математические методы и модели, приходится решать СЛАУ с любым числом неизвестных и любым числом уравнений.

Определение 2. Решением СЛАУ называют вектор столбец значений неизвестных, при которых равенство (4.2) становится верным.

СЛАУ может не иметь ни одного решения (несовместная СЛАУ), единственное решение или бесконечно много решений.

Решить СЛАУ – значит найти все ее решения или доказать ее несовместность.

Определение 3. Две или более СЛАУ называют равносильными, если все они несовместны или их решения совпадают.

4.2. Решение систем с квадратной матрицей

Наиболее простые методы решения имеют системы, число уравнений в которых равно числу неизвестных, то есть их главная матрица – квадратная.

Пусть в системе главная матрица системыесть квадратная матрица порядкаn, имеющая обратную матрицу . Умножим слева обе части равенства на матрицу:

.

Итак, для систем с квадратной матрицей, имеющей обратную, решение системы находят по формуле:

(4.3)

Таким образом, чтобы найти столбец неизвестных, надо матрицу, обратную главной матрице СЛАУ, умножить на столбец свободных членов.

Пример. Решить СЛАУ:

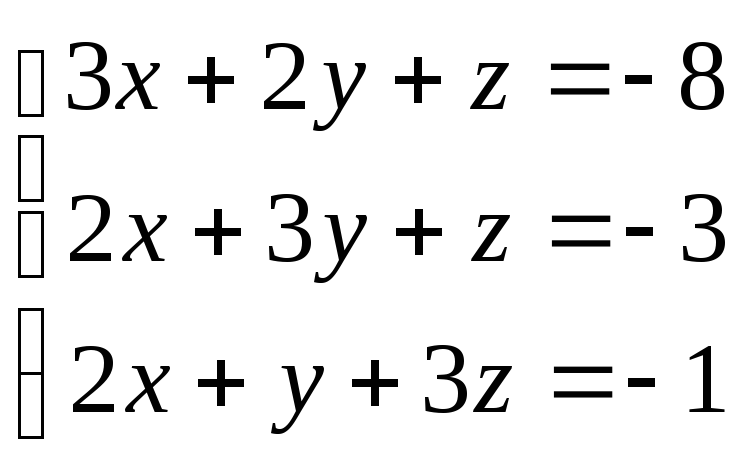
Решение.

Методом элементарных преобразований найдем матрицу, обратную главной матрице системы:

=~~~

~~ ~~~=.

;

.

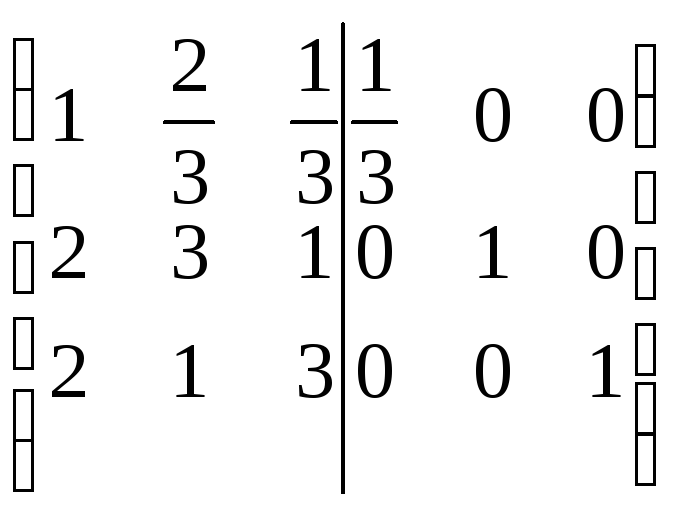Ответ:

Из формулы (4.3) вытекают формулы Крамера, позволяющие находить решение системы через вычисление нескольких определителей. Рассмотрим правую часть равенства (3). Матрицу запишем через присоединеную матрицу:

==,

где - алгебраическое дополнение элемента(). (См. стр. ).

Обозначим: .

Вычислим определители:

= =- разложение по первому столбцу;

= =- разложение по второму столбцу;

………………………………………………………………………………

= =- разложение поn-ному столбцу.

Получаем:

====,

или

(4.4)

Равенства (4.4) и есть формулы Крамера.

Определитель называютглавным определителем системы, определители -побочными определителями системы. Чтобы получить побочный определитель , надо в главной матрице системы заменить j-тый столбец столбцом свободных членов СЛАУ.

Чтобы найти неизвестное x_j надо разделить побочный определитель на главный определитель системы.

В заключение подчеркнем, что по формулам Крамера и с помощью обратной матрицы можно решать лишь системы с квадратной матрицей, определитель которой отличен от нуля.