3.5. Нахождение обратной матрицы

Определение матрицы, обратной данной квадратной матрице , приведено в разделе 3.2. В данном разделе рассмотрены методы нахождения обратной матрицы.

Основная формула:

(3.9)

где - алгебраическое дополнение элементаматрицы.

Обратим внимание на следующее:

1. Матрица =состоит из алгебраических дополнений элементов транспонированной матрицы. Такую матрицу называютприсоединенной матрицей..

2. Множитель перед матрицей - величина, обратная определителю матрицы. Из этого вытекает условие существования матрицы, обратной матрице .

Для того, чтобы матрицаимела обратную, необходимо и достаточно: .

Покажем справедливость формулы (1). По определению обратной матрицы: , гдеединичная матрица, того же порядка, что и. Рассмотрим произведение:

=.

Пусть -i-тая строка матрицы ,-j-тый столбец матрицы .

.

Действительно:

есть разложение поi-той строке, следовательно, . Если же, то. Это равнозначно тому, чтоj-тая строка матрицы заменена ее i-той строкой, то есть матрица имеет две одинаковых i-тых строки. Но по свойствам определителей (см. стр. ), определитель матрицы, имеющей две одинаковые строки, равен 0.

Следовательно:

=

=,

следовательно,

= =E.

Аналогично доказывается и вторая половина равенства: .

Пример.

Дана матрица . Найтии выполнить проверку.

Решение.

, ,

Проверка:

= =

==.

== ==.

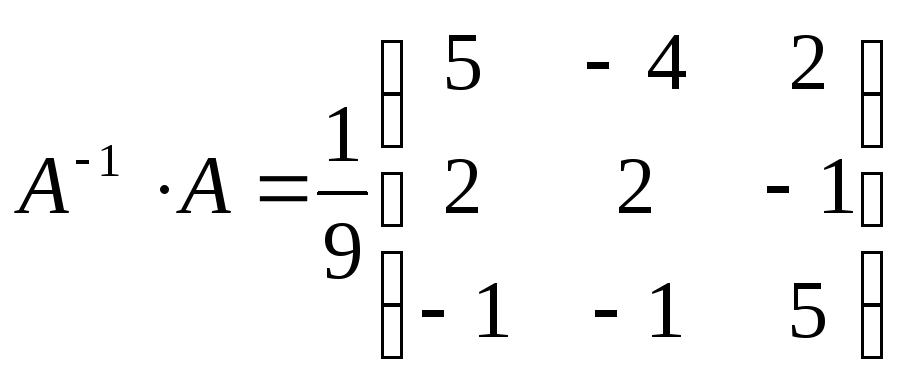
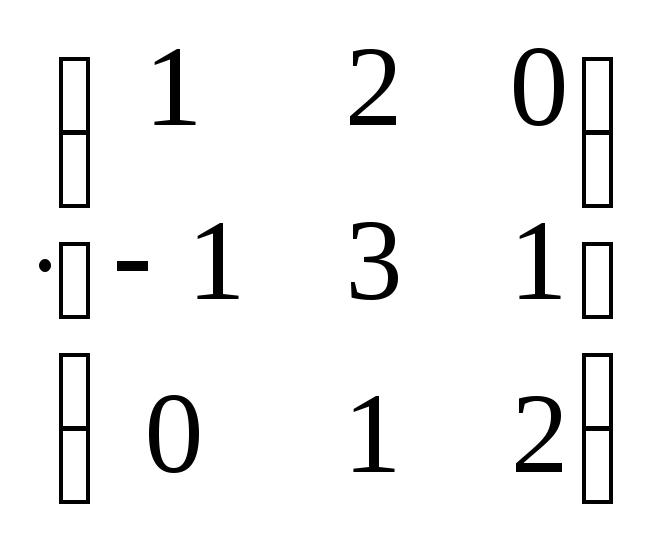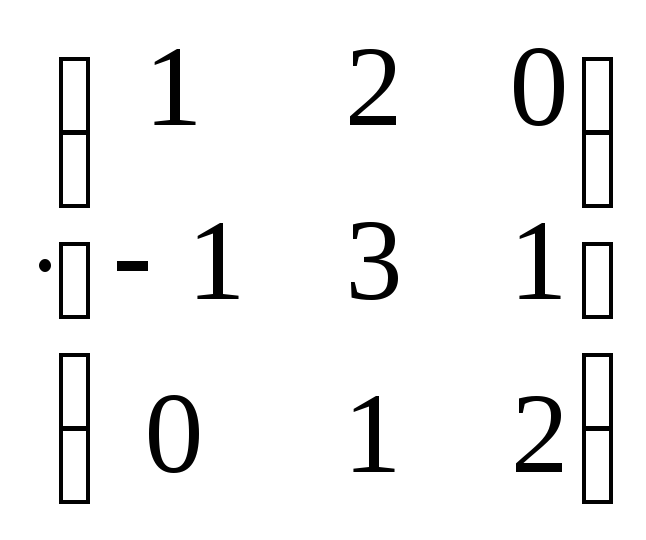
. Следовательно, найдена верно.

Получение обратной матрицы путем элементарных преобразований.

В курсах [ ] алгебры обоснован алгоритм получения обратной матрицы путем элементарных преобразований над ее строками. Рассмотрим последовательность шагов этого алгоритма на следующем примере.

Пример.

Найти матрицу, обратную матрице =.

Решение.

Шаг 0. Записать преобразуемую матрицу, состоящую из матрицы A и единичной матрицы Е:

.

Шаг 1. .

Шаг 2. Разрешающая строка - , разрешающий столбец -Переписать разрешающую строку. В разрешающем столбце записать:=1,. Применяя правило прямоугольника, преобразовать строки,,.

Шаг 3. Разрешающая строка - , разрешающий столбец -Переписать разрешающую строку. В разрешающем столбце записать:=1,. Применяя правило прямоугольника, преобразовать строки,,.

Шаг 3. .

Шаг 4.. Разрешающая строка - , разрешающий столбец -Переписать разрешающую строку. В разрешающем столбце записать:=1,. Применяя правило прямоугольника, преобразовать строки,,

Шаг 5.

Шаг 6.. Разрешающая строка - , разрешающий столбец -Переписать разрешающую строку. В разрешающем столбце записать:=1,. Применяя правило прямоугольника, преобразовать строки,,

Левая половина матрицы – единичная матрица  конец процедуры.

Правая половина матрицы есть :

=

Выполним проверку:

==

===E.

3.6. Ранг матрицы

Любую матрицу можно рассматривать как системуm векторов-строк или как системуn векторов-столбцов . Составляя всевозможные линейные комбинации векторов-строк и векторов-столбцов, получим линейные оболочки системы строк и системы столбцов матрицы, которые являются подпространствами пространствR^m и Rⁿ .Обозначим эти подпространства L и S соответственно. Размерности подпространств L и S равны соответственно максимальному числу линейно независимых строк матрицы и максимальному числу ее линейно независимых столбцов. В курсах линейной алгебры доказывается, что размерности подпространств L и S одинаковы: dimL = dimS = r. Число r называют рангом матрицы. Ранг матрицы – это основная числовая характеристика матрицы любого вида.

Определение1. Рангом матрицы называют максимальное число ее линейно независимых строк или максимальное число ее линейно независимых столбцов.

Обозначение: rangA= r – ранг матрицы A равен числу r.

Максимальное число линейно независимых строк и столбцов матрицы будем находить с помощью элементарных преобразований строк и столбцов. Отметим, что элементарные преобразования строк матрицы есть составление линейных комбинаций этих строк. Это означает, что, выполняя элементарные преобразования строк, мы остаемся в пространстве L. Аналогично, выполняя элементарные преобразования столбцов, остаемся в пространстве S. Другими словами, элементарные преобразования строк или столбцов матрицы не меняют ее ранга.

Определение 2. Матрицы, полученные одна из другой путем элементарных преобразований, строк или столбцов называют эквивалентными матрицами.

Обозначение: A~A’ - матрицы A и A’ эквивалентны.

Покажем на примере, как путем элементарных преобразований строк и столбцов можно найти размерность пространств L и S, иными словами, решить вопрос о ранге матрицы A.

Пример.

Найти размерность линейных оболочек строк и столбцов матрицы

.

Решение.

Будем выполнять элементарные преобразования строк матрицы, стремясь представить одни строки в виде линейных комбинаций других строк. После этих преобразований должно остаться максимальное число линейно независимых строк, то есть базис пространства L. Число строк в базисе и будет dimL=rangA. Элементарные преобразования будем выполнять, пользуясь правилом прямоугольника.

Шаг 1. Выберем разрешающую строку и разрешающий столбец матрицы A. На их пересечении будет стоять разрешающий элемент. В качестве разрешающего элемента удобно выбрать 1, поэтому в данном примере в качестве разрешающей строки удобно выбрать , а в качестве разрешающего столбца -. Тогда разрешающим элементом будет=1.

Шаг 2. Перепишем разрешающую строку. В разрешающем столбце все элементы, кроме , положим равными 0. Остальные элементы перепишем, пользуясь правилом прямоугольника:

~ .

Шаг 3. Выберем разрешающую строку и разрешающий столбец преобразованной матрицы A. Из соображений удобства разрешающей строкой выбираем , разрешающим столбцом -. Тогда разрешающим элементом будет= -1.

Шаг 4. Перепишем разрешающую строку, разделив ее на (-1). В разрешающем столбце все элементы, кроме , положим равными 0. Остальные элементы перепишем, пользуясь правилом прямоугольника:

.

Система строк () матрицыA линейно независима. В самом деле, нулевая линейная комбинация этих строк соответствует системе равенств:

.

Второе равенство этой системы выполняется лишь при условии , что влечет за собой:. Следовательно, система строк () имеет лишь вырожденную нулевую линейную комбинацию, а значит, она линейно независима. Остальные строкиматрицыA могут быть представлены как линейные комбинации строк .

Таким образом, в линейной оболочке L строк матрицы A выделен базис (), следовательно,dimL=rangA=2. Отметим, что в качестве базиса можно было бы взять какие-либо другие две строки матрицы A, однако, добавив к ним еще одну ее строку, вновь получили бы линейно зависимую систему.

Поменяем порядок столбцов преобразованной матрицы A, так, чтобы базисные столбцы встали на первое и второе места, а также опустим нулевые строки:

A~~~=

=.

Символ означает, что матрица разбита на две части: единичную матрицу второго порядка и матрицуB, размерности 23.

Аналогично найдем размерность линейной оболочки столбцов dimS.

~~.

Столбцы () образуют линейно независимую систему векторов столбцов. Остальные столбцы, соответствующие нулевым столбцам преобразованной матрицы, линейно через них выражаются. В качестве базиса линейной оболочкиS системы столбцов матрицы A, можно выбрать систему (). Следовательно,dimS= rangA =2.

Удалив нулевые столбцы из преобразованной матрицы, и поменяв местами первую и вторую строки, получим:

A~~~.

Символ означает, что матрица разбита на две части: единичную матрицу второго порядка и матрицуQ, размерности 22.

Обобщим выводы, вытекающие из рассмотрения примера, (примем их без доказательства):

1. Поскольку максимальное число линейно независимых строк матрицы равно максимальному числу ее линейно независимых столбцов, ранг матрицы можно находить либо путем элементарных преобразований строк, либо путем элементарных преобразований столбцов, руководствуясь соображениями удобства.

2. Любую матрицу можно привести к виду:, путем элементарных преобразований строк, или к виду:, путем элементарных преобразований столбцов, где:,;- единичная матрица порядкаr, - матрица, содержащаяr строк и (n-r) столбцов, - матрица, содержащая(n-r) строк и r столбцов. Если r=m, то =;. еслиr=n, то =.

3. Размерность линейной оболочки системы строк матрицы равна размерности линейной оболочки системы ее столбцов и равна рангу матрицы.