
- •Математика
- •Оглавление
- •1. Пространство геометрических векторов
- •Геометрический вектор. Длина и направление вектора. Равенство векторов
- •1.2. Линейные операции над векторами
- •1.3. Свойства линейных операций над геометрическими векторами
- •1.4. Линейная зависимость и линейная независимость систем
- •Доказательство
- •1.5. Скалярное произведение векторов
- •Решение
- •1.6. Векторное произведение векторов
- •1.7. Смешанное произведение векторов
- •2. Система координат. Арифметические векторы
- •2.1. Декартова прямоугольная система координат. Координаты вектора
- •2.2. Операции над арифметическими векторами
- •2.3. Линейные векторные пространства. Базис линейного пространства
- •3. Матрицы и определители
- •3.1. Матрицы, их классификация и линейные операции над ними
- •Равенство матриц
- •Умножение матрицы на число
- •Сложение матриц
- •3.2. Умножение матриц
- •Свойства умножения матриц
- •3.3. Определители. Общие методы их вычисления
- •1. Вычисление определителей второго порядка.
- •2. Вычисление определителей третьего порядка
- •3. Вычисление определителя порядка n
- •3.4. Свойства определителей. Методы вычисления, основанные на свойствах
- •3.5. Нахождение обратной матрицы
- •3.6. Ранг матрицы
- •4. Системы линейных алгебраических уравнений
- •4.1. Основные понятия и определения
- •4.2. Решение систем с квадратной матрицей
- •4.3. Решение слау методом Гаусса
- •Решение
- •4.4. Однородные слау и их решение
- •4.5. Обобщение теории слау
Свойства умножения матриц
Умножение матриц выполнимо, если число столбцов первой матрицы равно числу строк второй матрицы.
Умножение некоммутативно: существуют матрицы A и B, для которых
 .
Матрицы, для которых
.
Матрицы, для которых называюткоммутирующими
матрицами.
называюткоммутирующими
матрицами.Умножение ассоциативно
 .
.Умножение дистрибутивно относительно сложения:
![]() .
.
Если E – единичная матрица порядка n и
 -
прямоугольная матрица, содержащая n
строк и произвольное число столбцов,
то
-
прямоугольная матрица, содержащая n
строк и произвольное число столбцов,
то
 .
Если
.
Если
 -
прямоугольная матрица, содержащая n
столбцов и произвольное число строк,
то
-
прямоугольная матрица, содержащая n
столбцов и произвольное число строк,
то
 .
Если жеС
– квадратная матрица порядка n,
то
.
Если жеС
– квадратная матрица порядка n,
то
 .
Другими словами, единичная матрица
играет роль 1 в умножении чисел.
.
Другими словами, единичная матрица
играет роль 1 в умножении чисел.
Свойства умножения матриц принимаем без доказательства. Свойство 5 проиллюстрируем на примере.
Пример.
 .
.
Как
известно, если при умножении чисел
![]() ,
то число
,
то число![]() называют числом, обратным числу
называют числом, обратным числу![]() .
Обратного числа не имеет только
.
Обратного числа не имеет только![]() .
Во множестве квадратных матриц порядкаn
некоторые матрицы также имеют обратные.
.
Во множестве квадратных матриц порядкаn
некоторые матрицы также имеют обратные.
Определение
3. Матрицу
![]() называют
матрицей,обратной
матрице A,
если выполняются равенства:
называют
матрицей,обратной
матрице A,
если выполняются равенства:
![]() ,
гдеA
– квадратная матрица порядка n,
E – единичная
матрица порядка n.
,
гдеA
– квадратная матрица порядка n,
E – единичная
матрица порядка n.
Не всякая квадратная матрица имеет обратную. Условия существования обратной матрицы и алгоритмы ее нахождения рассматриваются в разделе 3.4.
3.3. Определители. Общие методы их вычисления
Определитель или детерминант квадратной матрицы – это одна из числовых характеристик матрицы. Определители используются при исследовании матриц, при решении систем уравнений и пр.
Обозначения определителей.
Пусть
![]() =
=![]() =
= - квадратная матрица порядкаn.
- квадратная матрица порядкаn.
 - определитель
матрицы D, определитель порядка n.
- определитель
матрицы D, определитель порядка n.
Обратим внимание на то, что в обозначении длины вектора и определителя матрицы использован один и тот же символ – прямые скобки:
![]() - вектор,
- вектор,
![]() - длина вектора, его числовая характеристика;
- длина вектора, его числовая характеристика;
![]() -
матрица,
-
матрица,
![]() -
определитель матрицы, ее числовая
характеристика.
-
определитель матрицы, ее числовая
характеристика.
В строгом определении понятия «определитель» используются такие понятия как «перестановка» и «подстановка», изучение которых выходит за рамки нашего курса8. Не давая строгого определения, покажем, как вычисляются определители различных порядков.
1. Вычисление определителей второго порядка.

![]() =
=
![]()
побочная диагональ главная диагональ
Пример.
![]() .
.
2. Вычисление определителей третьего порядка
 =
=
![]()
![]() .
.
Последовательность выполнения действий при вычислении определителя третьего порядка легко запомнить с помощью следующей схемы, которая называется Правилом треугольника для вычисления определителя третьего порядка.
Другое правило вычисления определителя третьего порядка называют Правилом разложения определителя по строке или столбцу. Оба эти правила представлены следующими таблицами.
Правило треугольника
|
+ |
- | |
|
главная диагональ
Сложить произведения элементов, стоящих на главной диагонали и в вершинах двух треугольников, одна из сторон которых параллельна главной диагонали |
побочная диагональ
Сложить произведения элементов, стоящих на побочной диагонали и в вершинах двух треугольников, одна из сторон которых параллельна побочной диагонали | |
|
Из первой суммы вычесть вторую |
| |
Разложение определителя по строке или столбцу
|
№ п/п |
Последовательность действий |
Выполнение действий |
Комментарии |
|
|
Выделить любойстолбец или строку определителя |
|
Выделен третий столбец |
|
2. |
Для каждого элемента выделенной строки или столбца составить определители второго порядка |
|
Полученные определители
Индексы i,jу
символа
|
|
3. |
Приписать каждому минору знаки «+» или «-» |
|
Полученные определители
|
|
4 |
Вычислить определитель |
|
|
Пример.
Вычислить
определитель:
 .
.
|
1). Применим правило треугольника: |
+
|
-
|
 =
=
=![]() .
.
2). Вычислим определитель разложением по третьей строке:
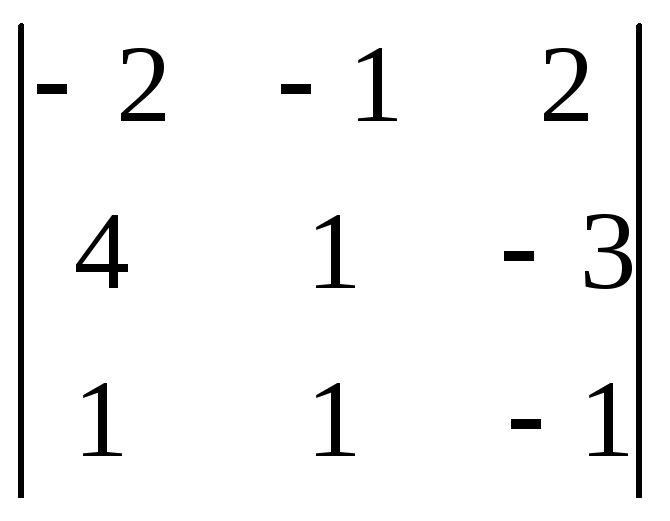
![]() =
=
=![]() .
.




 1.
1.






