Умножение матрицы на число

C=x C=

(3.4)

В сокращенной записи:



(3.5)

Отметим, что размерность матрицы вполне достаточно указывать один раз. Указание размерности сразу определяет возможные значения текущих индексов i,j.

Сложение матриц

Подчеркнем, что складывать можно лишь матрицы одинаковой размерности.

+=+= =

(3.6)

В краткой записи:

, 

(3.7)

Во множестве матриц одинаковой размерности линейные операции сложения и умножения на число обладают всеми свойствами, какими обладают эти операции над векторами (см. стр. ). Нулем во множестве матриц размерностиявляется матрица, все элементы которой – нули:

= =

(3.8)

Во многих задачах с использованием матриц исследуются части матриц – подматрицы. При составлении подматрицы порядок строк и столбцов основной матрицы не меняют, просто некоторые строки и столбцы вычеркивают.

Примеры.

1). =.

Матрица , размерности 53 имеет 6 квадратных подматриц порядка 3:

= ,=,=,

=,=,=.

2). Матрица Q= имеет 3 подматрицы размерности 23, 3 подматрицы размерности 32 и 9 квадратных подматриц порядка 2:

Номера вычеркнутой строки	Строка 3	Строка 2	Строка 1
Номер вычеркнутого столбца	Столбец 3	Столбец 2	Столбец 1
Номер вычеркнутого столбца Номер вы- черкнутой строки	столбец 3	столбец 2	столбец 1
строка 3
строка 2
строка 1

В таблице показано получение подматриц: вычеркивается либо строка матрицы Q, либо ее столбец, либо строка и столбец. В матрицах, полученных последним способом, индексы у символа Q, указывают номера вычекнутых строки и столбца.

3.2. Умножение матриц

Вопрос об умножении матриц начнем рассматривать с числового примера умножения матрицы строки на матрицу столбец.

Пример. .

Как видно из примера, произведение строки на столбец есть скалярное произведение арифметических векторов, первый из которых – вектор строка, второй вектор столбец. (См. стр.).

Если в матрице A n строк, а в матрице B m столбцов, то их произведение есть матрица AB, состоящая из скалярных произведений каждой строки матрицы A на каждый столбец матрицы B. Очевидно, что скалярное умножение строки на столбец выполнимо лишь в том случае, если число элементов строки равно числу элементов столбца. Это означает, что каждая строка матрицы A должна содержать столько же элементов, сколько содержит их каждый столбец B. Пусть и. В матрицеA n строк, каждая из которых содержит p элементов. В матрице B m столбцов, каждый из которых содержит q элементов. Чтобы умножение набыло выполнимо, необходимо, чтобыp=q.

Определение 2. Произведением матрицы на матрицуназывают матрицу , гдеесть скалярное произведениеi-той строки матрицы A на j-тый столбец матрицы B.

Пример.

1. .

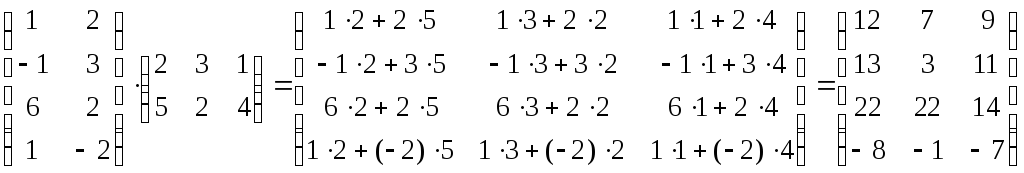2. .

Как видно из примера 2, произведением столбца на строку является квадратная матрица, порядок которой равен длине строки. В то же время произведение строки на столбец есть число.