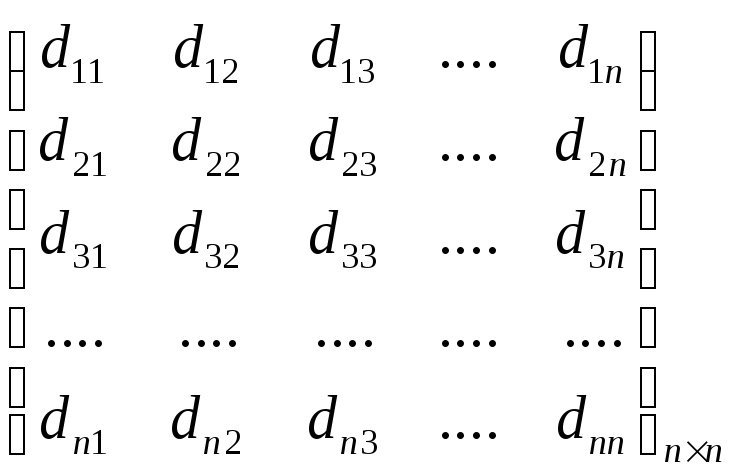3. Матрицы и определители

3.1. Матрицы, их классификация и линейные операции над ними

Систему n-мерных арифметических векторов () можно записать в виде таблицы, сделав их координаты либо строками, либо столбцами такой таблицы:

,

(3.1)

Определение 1. Матрицей, размерности pq называют прямоугольную таблицу чисел, содержащую p строк и q столбцов. Числа, из которых состоит матрица, называют элементами матрицы.

В формулах (3.1) участвуют матрицы, размерности kn и nk.

Правила записи матриц:

1). Матрицы обозначают большими латинскими буквами. Нижний индекс у буквы – размерность матрицы. Этот индекс можно опустить, если размерность матрицы известна.

2). Символ ^«T», как и ранее (см.стр. ), означает транспонирование, то есть замену строк столбцами.

3). Сама таблица чисел записывается в круглых скобках.

4). Если матрица не транспонирована, то первый индекс ее элемента, означает номер строки, второй - номер столбца.

Матрицы очень широко используются в математике, информатике, экономике и пр. Правила оперирования матрицами – один из вопросов линейной алгебры. Именно из линейной алгебры понятие матрицы пришло в другие области знаний .

Классификация матриц по размерности.

Название матрицы	Матрица столбец	Матрица строка	Прямоугольная матрица	Квадратная матрица
Вид матрицы
Пример

Квадратные матрицы играют особую роль в линейной алгебре. Рассмотрим их более детально. Прежде всего, отметим, что в случае квадратной матрицы говорят не о размерности матрицы , а опорядке матрицы, равном n.

У квадратной матрицы есть главная и побочная диагонали:

побочная диагональ главная диагональ

побочная диагональ главная диагональ

Классификация квадратных матриц

Название	Единичная матрица	Диагональная матрица	Треугольные матрицы
			верхнетреугольная	нижнетреугольная
Вид матрицы
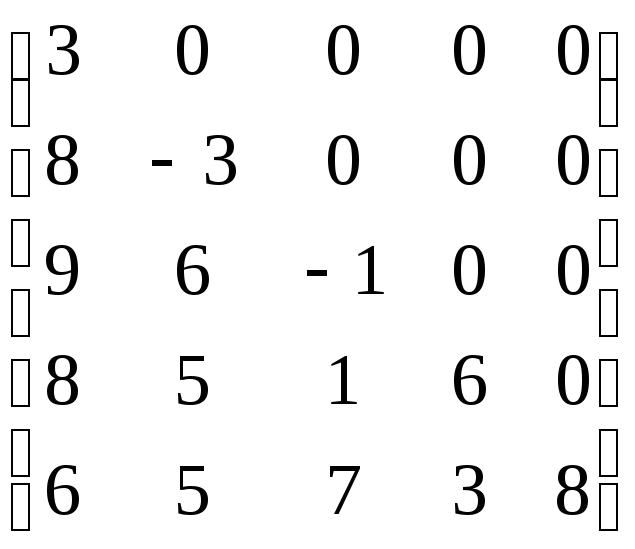
Пример	Единичная матрица четвертого порядка	Диагональная матрица четвертого порядка	Верхнетреугольная матрица третьего порядка	Нижнетреугольная матрица пятого порядка

Рассматривая матрицу как систему арифметических векторов, легко понять, что означает равенство матриц и как выполняются линейные операции над ними.

Равенство матриц

Две матрицы одинаковой размерности равны друг другу, если равны их соответствующие элементы⁷.

Для удобства записи утверждений, касающихся матриц, часто используют следующую символику:

(3.2)

где .

В такой записи символ «» – обозначение любого из элементов матрицы, индексыi,j - текущие индексы, переменные, пробегающие значения, . Развернутая формула (3.2) выглядит так:

=

(3.3)