
- •Математика
- •Оглавление
- •1. Пространство геометрических векторов
- •Геометрический вектор. Длина и направление вектора. Равенство векторов
- •1.2. Линейные операции над векторами
- •1.3. Свойства линейных операций над геометрическими векторами
- •1.4. Линейная зависимость и линейная независимость систем
- •Доказательство
- •1.5. Скалярное произведение векторов
- •Решение
- •1.6. Векторное произведение векторов
- •1.7. Смешанное произведение векторов
- •2. Система координат. Арифметические векторы
- •2.1. Декартова прямоугольная система координат. Координаты вектора
- •2.2. Операции над арифметическими векторами
- •2.3. Линейные векторные пространства. Базис линейного пространства
- •3. Матрицы и определители
- •3.1. Матрицы, их классификация и линейные операции над ними
- •Равенство матриц
- •Умножение матрицы на число
- •Сложение матриц
- •3.2. Умножение матриц
- •Свойства умножения матриц
- •3.3. Определители. Общие методы их вычисления
- •1. Вычисление определителей второго порядка.
- •2. Вычисление определителей третьего порядка
- •3. Вычисление определителя порядка n
- •3.4. Свойства определителей. Методы вычисления, основанные на свойствах
- •3.5. Нахождение обратной матрицы
- •3.6. Ранг матрицы
- •4. Системы линейных алгебраических уравнений
- •4.1. Основные понятия и определения
- •4.2. Решение систем с квадратной матрицей
- •4.3. Решение слау методом Гаусса
- •Решение
- •4.4. Однородные слау и их решение
- •4.5. Обобщение теории слау
2.3. Линейные векторные пространства. Базис линейного пространства
Понятия одно- двух- и трехмерного арифметических векторов может быть естественным образом обобщено на векторы любой размерности.
Определение 2.4. n-мерным арифметическим вектором называют последовательность n чисел – координат вектора.
Множество
всех n-мерных арифметических векторов,
координатами которых являются
действительные числа, обозначают Rn
![]() ,
Записывают n-мерные арифметические
векторы либо в виде строки:
,
Записывают n-мерные арифметические
векторы либо в виде строки:
|
|
(2.18) |
либо в виде столбца:
|
|
(2.19) |
Все основные понятия и все операции над одно-, двух- и трехмерными арифметическими векторами (разд. 2.2), за исключением векторного умножения, естественным образом обобщаются на векторы произвольной размерности. Однако в разд. 2.2 не был введен ряд важных понятий, характеризующих множества арифметических векторов любой размерности. Основным понятием векторной алгебры является понятие линейного векторного пространства, но прежде, чем ввести это понятие, дадим определение множества, замкнутого относительно операции.
Определение 2.5. Множество называют замкнутым относительно какой-либо операции, определенной в этом множестве, если в результате выполнения этой операции получают элемент этого же множества.
Примеры.
1. МножествоV2 геометрических векторов на плоскости замкнуто относительно операций умножения на число и сложения, так как, умножив вектор на любое число, сложив векторы или построив их линейную комбинацию, получим вектор, принадлежащий этой же плоскости. Однако относительно векторного умножения V2 не замкнуто, поскольку результат такой операции – вектор, перпендикулярный плоскости, в которой лежат векторы множители.
2.
Пусть V0
- множество векторов на прямой, имеющих
целочисленные координаты. (Например,
![]() ). V0
замкнуто относительно операции сложения:
складывая или вычитая целые числа, вновь
получают целое число. Однако V0
не замкнуто относительно умножения на
число: умножив вектор на дробное или
иррациональное число, целочисленной
координаты получить нельзя.
). V0
замкнуто относительно операции сложения:
складывая или вычитая целые числа, вновь
получают целое число. Однако V0
не замкнуто относительно умножения на
число: умножив вектор на дробное или
иррациональное число, целочисленной
координаты получить нельзя.
Понятие замкнутости множества относительно какой-либо операции относится не только к множествам векторов, но и, например, к множествам чисел. Так множество всех целых чисел замкнуто относительно операций сложения, вычитания и умножения, но не замкнуто относительно деления: поделив одно целое число на другое, не всегда получают целое число, может получиться дробь. Множество всех действительных чисел замкнуто относительно деления, если из него исключить число нуль (на нуль делить нельзя).
Пусть L множество n-мерных арифметических векторов, координатами которых являются действительные числа. Определены операции умножения вектора на число и сложения векторов, обладающие свойствами 1-8 (см. разд. 1.3).
Определение 2.6. Множество векторов L называют линейным векторным пространством над полем действительных чисел6, если L замкнуто относительно операций умножения на число и сложения.
Пусть
![]() - n-мерные векторы.. Рассмотрим линейную
комбинацию этих векторов:
- n-мерные векторы.. Рассмотрим линейную
комбинацию этих векторов:
|
|
(2.19) |
где
![]()
Пусть все векторы, участвующие в равенстве (2.19), – это векторы столбцы, то есть:
 ,
,
 ,
, ,…..
,….. .
.
Обратим внимание на двойную индексацию координат векторов: первый индекс – номер координаты, второй – номер вектора.
Перепишем равенство (2.19) в следующем виде:
 +
+ +
+ +…….+
+…….+
Учитывая определение равенства арифметических векторов, последнее равенство можно переписать следующим образом:
|
|
(2.20) |
Систему равенств (2.20) можно рассматривать с различных точек зрения:
1.
Если заданы все векторы
![]() и все числа
и все числа![]() (i=1,2,3,…n;
j=1,2,3,…k),
то с помощью системы равенств (2.20)
вычисляются координаты вектора
(i=1,2,3,…n;
j=1,2,3,…k),
то с помощью системы равенств (2.20)
вычисляются координаты вектора
![]() .
.
2.
Если заданы все векторы
![]() и вектор
и вектор
![]() ,
то система (2.20) - это система n
линейных алгебраических уравнений с k
неизвестными x1,
x2,
x3,…..xk
. Системы
такого вида и их решение рассмотрены в
разделе 4.
Из школьного курса алгебры известно,
что при решении системы линейных
уравнений реализуется одна из следующих
возможностей: (а) система имеет единственное
решение, (б) система имеет бесконечно
много решений, (в) система не имеют ни
одного решения. В связи с этим решение
системы (2.19) позволяет ответить на
вопросы:
,
то система (2.20) - это система n
линейных алгебраических уравнений с k
неизвестными x1,
x2,
x3,…..xk
. Системы
такого вида и их решение рассмотрены в
разделе 4.
Из школьного курса алгебры известно,
что при решении системы линейных
уравнений реализуется одна из следующих
возможностей: (а) система имеет единственное
решение, (б) система имеет бесконечно
много решений, (в) система не имеют ни
одного решения. В связи с этим решение
системы (2.19) позволяет ответить на
вопросы:
может ли вектор
 быть представлен как линейная комбинация
векторов
быть представлен как линейная комбинация
векторов
 ?
?единственно ли такое представление?
3.
Если заданы векторы
![]() ,
то система (2.19) определяетлинейную
оболочку множества векторов
(
,
то система (2.19) определяетлинейную
оболочку множества векторов
(![]() ).
).
Определение 2.5. Линейной оболочкой множества векторов называют множество всех линейных комбинаций этих векторов.
Линейную оболочку множества M принято обозначать [M].
Справедливо следующее утверждение:
Утверждение 1 Если M - какое-либо (любое) множество векторов из Rn , то линейная оболочка множества M замкнута относительно операций умножение на число и сложения векторов.
Доказательство.
Пусть M={![]() }.
Векторы из [M]
– это векторы, координаты которых
определяются системой (1.19), если переменные
}.
Векторы из [M]
– это векторы, координаты которых
определяются системой (1.19), если переменные
![]() пробегают
все возможные значения из R. Возьмем два
любых вектора из [M]:
пробегают
все возможные значения из R. Возьмем два
любых вектора из [M]:
![]()
![]() и
и![]()
![]() .
.
Сумма этих векторов:
![]() +
+![]() =
=
=![]()
является
вектором из [M],
так как
![]() ,
а значит,
,
а значит,![]() есть линейная комбинация векторов
есть линейная комбинация векторов
![]() .
.
Аналогично
доказывается, что, умножив вектор
линейной оболочки множества M
на любое действительное число, вновь
получим линейную комбинацию векторов
![]() ,
то есть вектор из [M].
Это и означает, что [M]
является замкнутым относительно операций
сложения и умножения на число.
,
то есть вектор из [M].
Это и означает, что [M]
является замкнутым относительно операций
сложения и умножения на число.
Обратим внимание на то, что в доказательстве использованы в неявном виде следующие свойства линейных операций над векторами: коммутативность сложения, ассоциативность сложения, дистрибутивность умножения относительно сложения чисел, смешанная ассоциативность.
Докажите
замкнутость линейной оболочки множества
 ,
обосновывая переходы от одного равенства
к другому ссылками на соответствующие
свойства.
,
обосновывая переходы от одного равенства
к другому ссылками на соответствующие
свойства.
Какой бы n-мерный вектор мы ни взяли, это будет вектор из пространства Rn. Но как было показано, линейная оболочка системы векторов из Rn замкнута относительно операций сложения и умножения на число, а следовательно, сама является пространством. Любая система n-мерных векторов является подмножеством множества векторов Rn, а линейная оболочка такой системы – линейным подпространством пространства Rn.
Отметим,
что линейная оболочка системы векторов,
состоящая из одного нуль-вектора,
является подпространством Rn,
хотя и состоит из одного лишь вектора
![]() .
Подпространство, состоящее из одного
нуль-вектора, называют вырожденным
подпространством.
.
Подпространство, состоящее из одного
нуль-вектора, называют вырожденным
подпространством.
Над линейными подпространствами определены операции сложения, пересечения и объединения.
Определение
2.6. Суммой
линейных подпространств L1
и L2
пространства Rn
называют множество L1+L2
всех векторов из Rn
вида:
![]() ,
где
,
где![]() .
.
Определение
2.7. Пересечением
линейных подпространств L1
и L2
пространства Rn
называют множество векторов
![]() ,
состоящее из общих векторов пространствL1
и L2.
,
состоящее из общих векторов пространствL1
и L2.
Определение
2.8. Объединением
линейных подпространств L1
и L2
пространства Rn
называют множество векторов
![]() ,
состоящее из всех векторов, принадлежащих
,
состоящее из всех векторов, принадлежащих![]() или
или![]() .
.
Встает
вопрос о ранжировании подпространств.
В случае геометрических пространств
вопрос этот интуитивно ясен: прямая
«больше» точки, размерность пространства
V1
равна 1. Плоскость «больше» прямой,
размерность пространства V2
равна 2. Все геометрическое пространство
векторов «больше» плоскости, размерность
V3
равна 3. Все векторы на прямой есть
линейные комбинации единственного
базисного вектора, например, вектора
![]() ,
на плоскости – системы двух базисных
векторов (
,
на плоскости – системы двух базисных
векторов (![]() ),
в пространстве – системы трех базисных
векторов (
),
в пространстве – системы трех базисных
векторов (![]() ).
).
Таким образом, размерность пространства равна числу базисных векторов. Определение базиса векторного пространства геометрических векторов было введено через понятие максимальной системы линейно независимых или свободных векторов (см. Определение 1.15). Аналогично можно ввести понятие базиса и размерности линейного векторного пространства в общем случае. Потребуются следующие понятия
Нулевая линейная комбинация системы векторов (
 ):
):
|
|
(2.21) |
Вырожденная линейная комбинация системы векторов (
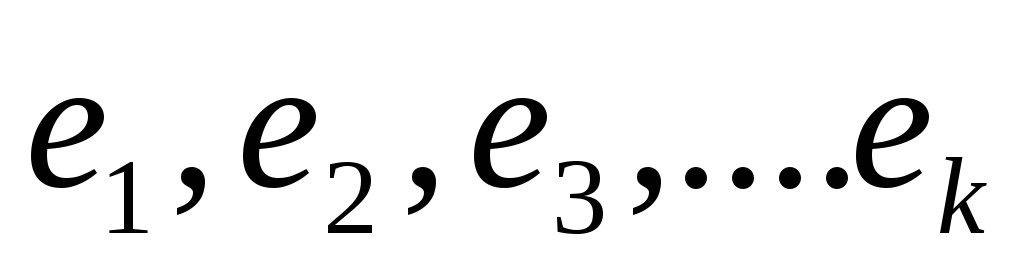 ):
):
|
|
(2.22) |
Очевидно, что вырожденная линейная комбинация всегда является нулевой, но, как и в случае геометрических векторов, обратное утверждение не всегда верно: существуют нулевые невырожденные линейные комбинации.
3.
Линейная
зависимость и линейная независимость
системы векторов (![]() ):
систему векторов (
):
систему векторов (![]() )
называют линейно независимой или
свободной, если ни один из векторов
системы не может быть представлен
линейной комбинацией других ее векторов.
В противном случае систему называют
линейно зависимой.
)
называют линейно независимой или
свободной, если ни один из векторов
системы не может быть представлен
линейной комбинацией других ее векторов.
В противном случае систему называют
линейно зависимой.
Как и в случае систем геометрических векторов, справедливо следующая теорема.
Теорема
1. Если
существует
невырожденная нулевая линейная комбинация
системы векторов (![]() )
, то система векторов является линейно
зависимой, если же единственной нулевой
комбинацией векторов системы является
вырожденная комбинация, то система
является свободной.
)
, то система векторов является линейно
зависимой, если же единственной нулевой
комбинацией векторов системы является
вырожденная комбинация, то система
является свободной.
Эта теорема, как и ее доказательство полностью повторяет соответствующую теорему в разделе 1.4. Для арифметических векторов, также, как и для геометрических, справедливы утверждения 1-4, вытекающие из этой теоремы (см. стр )
На основании Теоремы 1, вопрос о линейной зависимости или линейной независимости системы n-мерных арифметических векторов может быть решен с помощью системы уравнений:
|
|
(2.23) |
Отметим,
что в правой части системы (2.23) все числа
–нули. Такая система называется
однородной
линейной системой алгебраических
уравнений.
Очевидно, что однородная система имеет
по крайней мере одно решение - нулевое:
![]() .
Таким образом, вопрос о линейной
зависимости и линейной независимости
системы векторов, сводится к вопросу о
решении однородной системы уравнений:
если (2.23) имеет только нулевое решение,
то система векторов (
.
Таким образом, вопрос о линейной
зависимости и линейной независимости
системы векторов, сводится к вопросу о
решении однородной системы уравнений:
если (2.23) имеет только нулевое решение,
то система векторов (![]() )
свободна, если же имеются ненулевые
решения, то система векторов линейно
зависима.
)
свободна, если же имеются ненулевые
решения, то система векторов линейно
зависима.
4. Максимальная свободная система векторов.
Определение этого понятия для пространства арифметических векторов полностью совпадает с его определением для пространства геометрических векторов (см. определение 1.14, стр ). Однако следует помнить, что геометрический вектор не может иметь более трех измерений, поэтому в любом пространстве геометрических векторов максимальная свободная система содержит не более трех векторов. Размерность арифметического вектора может быть любой, а вопрос о числе векторов в максимальной свободной системе решается с помощью систем уравнений. Решение этого вопроса рассмотрено в разделе 4.
Согласно определению максимальной свободной системы векторов пространства, добавление в нее любого вектора пространства делает систему базисных векторов линейно зависимой.
Пусть
(![]() )
- максимальная свободная система
векторов линейного векторного пространства
L
и
)
- максимальная свободная система
векторов линейного векторного пространства
L
и
![]() ,
но
,
но![]() (
(![]() ).
В силу линейной независимости этих
векторов, однородная система уравнений
(2.23) имеет единственное решение –
нулевое.
).
В силу линейной независимости этих
векторов, однородная система уравнений
(2.23) имеет единственное решение –
нулевое.
Докажем справедливость утверждения:
Утверждение
1. Любой
вектор
![]() можно представить как линейную комбинацию
векторов максимальной свободной системы
векторов этого пространства (
можно представить как линейную комбинацию
векторов максимальной свободной системы
векторов этого пространства (![]() ),
или по-другому,
разложить
его по векторам (
),
или по-другому,
разложить
его по векторам (![]() ).
).
Пусть
сначала
![]() .
Система векторов (
.
Система векторов (![]() )
линейно зависима, то есть существует
их невырожденная нулевая линейная
комбинация:
)
линейно зависима, то есть существует
их невырожденная нулевая линейная
комбинация:
![]() ,
в которой среди чисел
,
в которой среди чисел![]() есть
хотя бы одно число отличное от нуля, а
следовательно, система уравнений
есть
хотя бы одно число отличное от нуля, а
следовательно, система уравнений
|
|
(2.24) |
помимо
нулевого, имеет хотя бы одно ненулевое
решение. Пусть в ненулевом решении
системы (2.24) y=0.
В этом случае система (2.24) обращается в
систему (2.23), имеющую единственное
решение – нулевое, а значит все xi
(i=1,2,3,…..k) в
этом решении также равны 0. Таким образом,
равенство
y=0 возможно
лишь в случае нулевого решения системы
(2.24), а чтобы
решение было ненулевым необходимо
условие:
![]() .
Отсюда следует, что
.
Отсюда следует, что
![]() есть линейная
комбинация
системы
векторов
(
есть линейная
комбинация
системы
векторов
(![]() ):
):
|
|
(2.25) |
где
![]() .
.
Если
![]() ,
то в системе (2.23)у
может быть любым числом. Положив
,
то в системе (2.23)у
может быть любым числом. Положив
![]() ,
вектор
,
вектор
![]() также можно записать в виде (2.25).
также можно записать в виде (2.25).
Утверждение 1 доказано.
Утверждение
2. Разложение
![]() =
=![]() вектора
вектора
![]() по
векторам (
по
векторам (![]() )
является единственным.
)
является единственным.
(Другими
словами, других чисел, помимо
![]() ,
не существует).
,
не существует).
Докажем
Утверждение
2 методом от
противного. Предположим, что помимо
набора чисел
![]() существует другой набор чисел
существует другой набор чисел![]() ,
таких, что
,
таких, что
![]() =
=![]() .
.
Получим:
![]() -
-![]() =
=![]() =(
=(![]() )
- (
)
- (![]() )=
)=
=(![]() .
.
В
силу линейной независимости системы
векторов (![]() )
, любая их нулевая линейная комбинация
является вырожденной, следовательно:
)
, любая их нулевая линейная комбинация
является вырожденной, следовательно:
![]()
![]() .
.
Это
и означает, что другого набора чисел,
помимо
![]() не существует.
не существует.
Определение 2.10. Базис линейного векторного пространства L – это любая максимальная свободная система векторов пространства L .
Определение 2.11. Число векторов в базисе линейного векторного пространства L называют размерностью пространства L.
Размерность пространства L обозначают: dimL.
Любой вектор из L можно единственным образом разложить по базисным векторам. Числовые коэффициенты в этом разложении называют координатами вектора в данном базисе.
Пусть
![]() -n-мерный
вектор. Все векторы вида:
-n-мерный
вектор. Все векторы вида:
![]() ,
где
,
где![]() ,
образуют линейную оболочку вектора
,
образуют линейную оболочку вектора![]() ,
которая замкнута относительно операций
сложения и умножения на число, а
следовательно образует линейное
векторное пространствоL1
=[
,
которая замкнута относительно операций
сложения и умножения на число, а
следовательно образует линейное
векторное пространствоL1
=[![]() ].
Единственным базисным вектором этого
пространства является вектор
].
Единственным базисным вектором этого
пространства является вектор![]() .СледовательноdimL1
=1. С
геометрической точки зрения, L1
– это числовая прямая, и
.СледовательноdimL1
=1. С
геометрической точки зрения, L1
– это числовая прямая, и
![]() -
направленный отрезок единичной длины,
приложенный к точкеO.
(См. стр. ).
-
направленный отрезок единичной длины,
приложенный к точкеO.
(См. стр. ).
Пусть
![]() и
и![]() - два неколлинеарных вектора. Каждый из
них образует линейное пространство
размерности 1:L’1
=[
- два неколлинеарных вектора. Каждый из
них образует линейное пространство
размерности 1:L’1
=[![]() ]
иL’’1
=[
]
иL’’1
=[![]() ],dimL’1
=
dimL’’1=1.
В геометрическом пространстве они
соответствуют двум непараллельным
прямым.
Составляя
всевозможные линейные комбинации
системы векторов (
],dimL’1
=
dimL’’1=1.
В геометрическом пространстве они
соответствуют двум непараллельным
прямым.
Составляя
всевозможные линейные комбинации
системы векторов (![]() ,
,![]() ):
):![]()
![]() ,
получим линейную оболочкуL2
=[
,
получим линейную оболочкуL2
=[![]() ,
,![]() ],
которая является линейным пространством
размерности 2, аL’1
и L’’1
– его подпространствами. В геометрических
терминах L2
представляет
плоскость, проходящую через две
пересекающиеся прямые.
],
которая является линейным пространством
размерности 2, аL’1
и L’’1
– его подпространствами. В геометрических
терминах L2
представляет
плоскость, проходящую через две
пересекающиеся прямые.
Аналогично
строятся пространства
![]() ,
,![]() …..
…..![]() ,
размерности которых 3, 4,….n
соответственно. Отметим, что, начиная
с
,
размерности которых 3, 4,….n
соответственно. Отметим, что, начиная
с
![]() геометрическая
интерпретация неприменима. Математика,
наряду с конечномерными, занимается
изучением и бесконечномерных линейных
пространств, однако бесконечномерные
линейные пространства в нашем курсе не
рассматриваются.
геометрическая
интерпретация неприменима. Математика,
наряду с конечномерными, занимается
изучением и бесконечномерных линейных
пространств, однако бесконечномерные
линейные пространства в нашем курсе не
рассматриваются.
Справедлива Теорема, которую принимаем без доказательства.
Теорема
о конечномерных пространствах.
Пусть L
– конечномерное пространство и (![]() )
– его базис. Тогда:
)
– его базис. Тогда:
(1) все базисы L конечны и состоят из k векторов;
(2) любая система векторов L, состоящая более, чем из k векторов, линейно зависима;
(3) всякая свободная система, состоящая из k векторов, является базисом пространства L;
(4)
произвольную свободную систему векторов,
состоящую из m
векторов, где m<k,
можно дополнить (k
- m) векторами
из (![]() )
до базиса пространстваL.
)
до базиса пространстваL.
В
пространстве Rn
часто используется ортонормированный
базис, примером которого может служить
последовательность векторов (![]() ):
):
![]() =
=![]() ,
,![]() =
=![]() ,
,![]()
![]() ….
….![]() =
=![]() .
.
Норма каждого из этих векторов равна 1, а скалярное произведение любых двух векторов равна 0.



