
Пу-112 КТэ 2 сем / Математика / КЗ для Филиппова
.docxЗадания 11- 20.
Даны точки А(2; 0; 1) В(-1; 0; 0) С (0; 2; 3) S(3; 2; 1).
По данным точкам построить пирамиду в системе координат и найти:
-
длину ребра АВ;
-
угол межlу ребрами АВ и АS;
-
площадь основания пирамиды;
-
объем пирамиды;
-
уравнение прямой АВ;
-
уравнение плоскости АВС;
-
угол наклона ребра АS к основанию пирамиды;
-
проекцию вершины S на плоскость АВС;
-
длину высоты пирамиды.
-
Длина ребра

 =
=

= =
=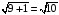 .
.
-
Угол между ребрами или


-
Найдем векторы
 и
и
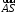
 =(-1-2;
0-0; 0-1) = (-3; 0; -1)
=(-1-2;
0-0; 0-1) = (-3; 0; -1) 
 =(3-2;
2-0; 1-1) = (1; 2; 0)
=(3-2;
2-0; 1-1) = (1; 2; 0)
 =
-3
=
-3 1+
0
1+
0 2
- 1
2
- 1 0 = -3;
0 = -3;
 =
=
 ;
;
 =
=
 =
=


 ;
;
 =
=
 ;
;
-
Найдем площадь
 –
основание пирамиды.
–
основание пирамиды.
 ,
где
,
где
 –
векторное
произведение.
–
векторное
произведение.
По
формуле
 =
=
 Найдем
Найдем
 =
=
 =
=

 =
=
=
 .
.

=
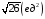 .
.
4)
Объем пирамиды
 ,
применяя смешанное произведение
векторов, по формуле
,
применяя смешанное произведение
векторов, по формуле

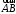 =
(-3;
0; 1)
=
(-3;
0; 1)
 = (1; 2; 0)
= (1; 2; 0)
 = (-2; 2; 2)
= (-2; 2; 2)

 =
=
 .
.
-
Известны точки
 и
и
 .
.
Уравнение прямой, проходящей через две данные точки имеет вид


Получим каноническое уравнение прямой :
 ,
в котором известен направляющий вектор
прямой
,
в котором известен направляющий вектор
прямой

-
Уравнение плотности
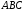 составим
по формуле
составим
по формуле
 ,
где
,
где



Подставим
координаты точек
 в
данное уравнение
в
данное уравнение
 .
.
 или
или

 .
.
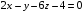 из
полученного уравнения запишем координаты
нормального вектора
из
полученного уравнения запишем координаты
нормального вектора

-
Дадим иллюстрацию для решения задачи 7)





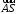




8)Запишем
уравнение прямой, проходящей через
точку S перпендикулярно
плоскости ABC:

 –
координаты
вектора, параллельного данной прямой
и перпендикулярного плоскости
ABC.
Это вектор
–
координаты
вектора, параллельного данной прямой
и перпендикулярного плоскости
ABC.
Это вектор
 .
.
 –
координаты
точки S
–
координаты
точки S
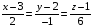
Проекцию
вершины S
на плоскость ABC
найдем
как точку пересечения прямой и плоскости
из решения системы





Подставим
 в уравнение плоскости
в уравнение плоскости
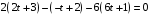





 Итак
Итак
 – искомая точка пересечения.
– искомая точка пересечения.
-
Длину высоты пирамиды H можно найти из формулы:

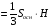


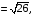
Значит
 ,
тогда
,
тогда
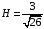
Задания 51 – 60
Дана система линейных уравнений




Решим систему а) матричным методом, б) методом Крамера, в) методом Гаусса.
а)
Данной соответствует матричное уравнение
 ,
которое решается по формуле:
,
которое решается по формуле:
 .
Матрицы имеют вид:
.
Матрицы имеют вид:



Находим
обратную матрицу

 =
=




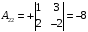




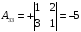
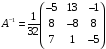 Находим
матрицу
Находим
матрицу
 .
.



 .
.
б)
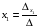 ;
;
 ;
;
 – формулы Крамера. Вычислим все
определители
– формулы Крамера. Вычислим все
определители





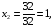

в) Метод Гаусса
Составим
расширенную матрицу
 и
преобразуем ее с помощью элементарных
преобразований.
и
преобразуем ее с помощью элементарных
преобразований.







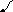
Из
полученной матрицы, выделяя последнюю
строку, видим, что исключены неизвестные
 и
и
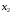 .
Найдем
.
Найдем
 .
.
 ,
,
 .
.
Вторая
строка соответствует уравнению
 или
или
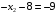 ;
;
 ,
,
 .
.
Аналогично
из первой строки запишем уравнение


 .
.
Итак


 .
.
Для решения задач 11 – 20 и 51– 60 рекомендуется учебное пособие П.Е. Данко., А.Г. Попов, Т.Я. Кожевникова «Высшая математика в упражнениях и задачах», ч.1 М.: Оникс 21 век. 2005, гл. I – IV стр. 39 – 91.
Задания 91 – 100
Дано
комплексное число
 .
Записать число
.
Записать число
 в
алгебраической и тригонометрической
формах и найти все корни уравнения
в
алгебраической и тригонометрической
формах и найти все корни уравнения
 .
.
Рекомендуемая литература П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова «Высшая математика в упражнениях и задачах», ч. II гл. III §7 стр. 97 – 101.
Найдем
алгебраическую форму комплексного
числа
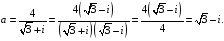
Тригонометрическая
форма комплексного числа
 определяется
по формуле
определяется
по формуле

Изобразив
число на плоскости, найдем
 и
и .
.



Итак,
число
 .
.
Найдем
корни уравнения

 .
.
 =
= ,
,
 .
.

при
 =0
=0
 ,
,
при



 ,
,
при


 .
.
Задания 111 – 120
Вычислить пределы.
а)
 За скобку выносим наивысшую степень
За скобку выносим наивысшую степень
 для
числителя и знаменателя.
для
числителя и знаменателя.

б)



Для
исключения неопределенности
 требуется числитель и знаменатель
разложить на множители.
требуется числитель и знаменатель
разложить на множители.
в)

В
данном случае для исключения
неопределенности
 использованы эквивалентные бесконечно
малые, например
использованы эквивалентные бесконечно
малые, например
 ,
,

г)

= .
.
д)



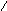
=



Задания 131 – 140
Задана
функция
 .
Найти точки разрыва, если они существуют.
Сделать чертеж.
.
Найти точки разрыва, если они существуют.
Сделать чертеж.
если
 <
1
<
1
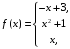 ,
если
,
если
 <
2
<
2
если

Кусочно – заданная функция представлена функциями, непрерывные на данных интервалах.
Проверим непрерывность в граничных точках.
 Найдем
односторонние пределы
Найдем
односторонние пределы


 ;
;

Левосторонний
и правосторонний пределы равны и равны
значению функции в точке
 .
Значит функция в этой точке непрерывна.
.
Значит функция в этой точке непрерывна.
 Аналогично
Аналогично

 5,
5,

 .
.
Пределы
различны, значит в точке
 функция
имеет разрыв с конечным скачком.
функция
имеет разрыв с конечным скачком.
График функций выполните самостоятельно.
Обратите внимание на вспомогательное учебное пособие П.Е. Данко., А.Г. Попов, Т.Я. Кожевникова «Высшая математика в упражнениях и задачах», ч.1 гл. V1 §§ 4 – 6.
Задание 141– 150
Найти
производные
 следующих функций:
следующих функций:
а)

 ;
б)
;
б)
 ;
;
в)
 ;
г)
;
г)
 ;
;
д)
 .
.
а)
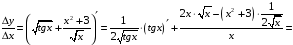
= .
.
б)

=
в)

г)
 .
.
Прологарифмируем обе части равенства
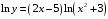
Продифференцируем обе части
 ;
;
 ;
;
 ;
;

д)
 ;
;
Функция
 задана
не явно.
задана
не явно.
 ;
;
 ;
;
 ;
;
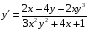 .
.
