
- •Задания к контрольной работе по дисциплине
- •Комплекты контрольных работ по дисциплине «Математика» для студентов заочной формы обучения по профилизациям Комплект заданий 1
- •Комплект заданий 2
- •1. Элементы линейной алгебры и аналитической геометрии
- •2. Производная и её приложение
- •2. Приложения дифференциального исчисления
- •6. Дифференциальное исчисление функций нескольких переменных
- •7. Неопределённый и определённыё интегралы
- •8. Дифференциальные уравнения
- •9. Двойные и криволинейные интегралы
- •9. Ряды
- •10. Операционное исчисление
- •11. Теория вероятностей и математическая статистика
- •521-530.
- •Задания для выполнения контрольной работы по дисциплине
2. Производная и её приложение
141-150.
Найти производные
![]() данных функций.
данных функций.
141.
а)
 ;
б)
;
б)![]() ;
;
в)
![]() ;
г)
;
г)
![]() ; д)
; д)
 .
.
142.
а)
![]() ; б)
; б) ; в)
; в)![]() ;
;
г)
![]() ;
д)
;
д)
![]() .
.
143.
а)
 ;
б)
;
б)
 ;
в)
;
в)
![]() ;
;
г)
![]() ; д)
; д)
![]() .
.
144.
а)
 ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ; д)
; д)
 .
.
145.
а)
 ; б)
; б) ; в)
; в) ;
;
г)
![]() ; д)
; д)
![]() .
.
146.
а)
 ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ; д)
; д)
![]() .
.
147.
а)
 ; б)
; б)
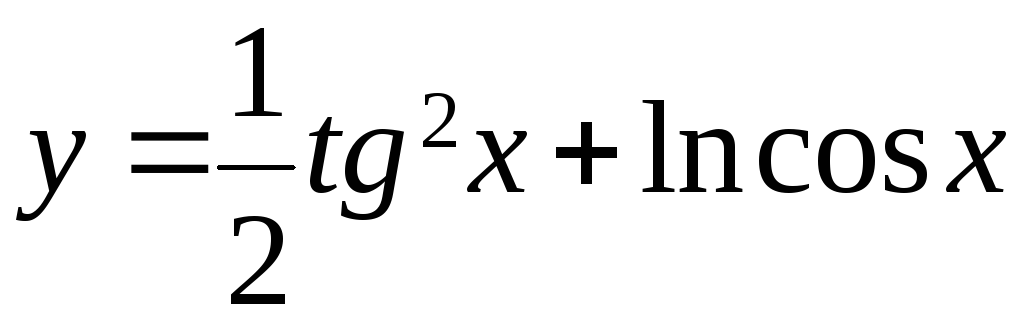 ;
;
в)
 ;
г)
;
г)![]() ;
;
д)
![]() .
.
148.
а)
 ; б)
; б) ;
;
в)
![]() ; г)
; г)
![]() ;
д)
;
д)
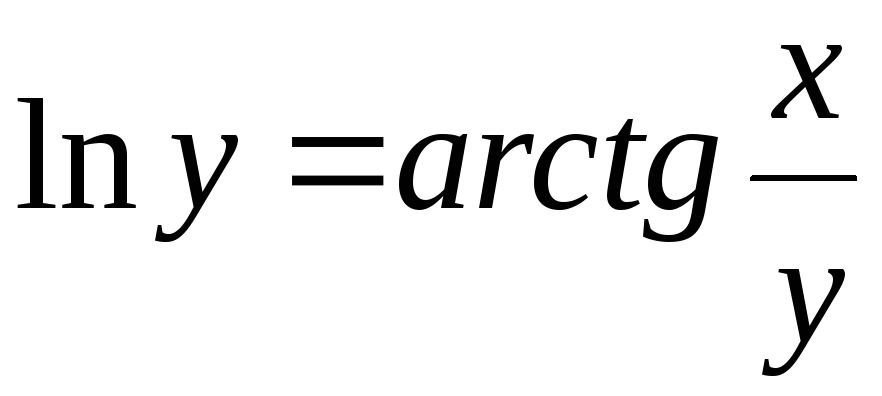 .
.
149.
а)
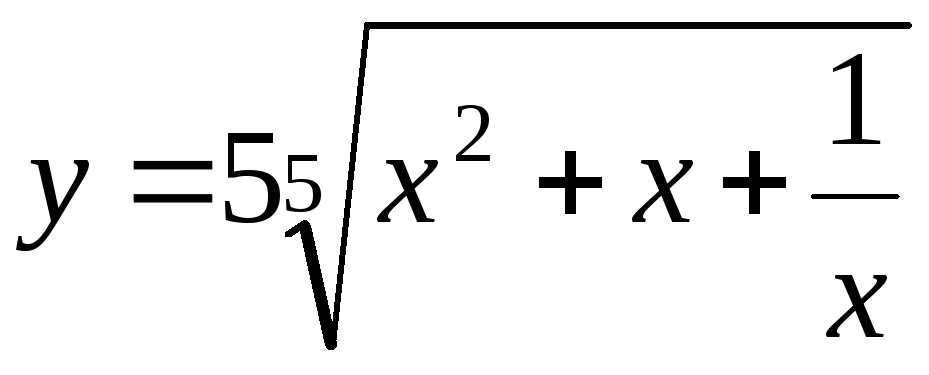 ;
б)
;
б)
![]() ;
в)
;
в)
 ;
;
г)
![]() ; д)
; д)
![]() .
.
150.
а)
![]() ; б)
; б)
 ;
;
в)
 ;
г)
;
г)
![]() ;
;
д)
![]() .
.
151-160.
Найти
![]() и
и
![]() .
.
151.
а)
 ; б)
; б) .
.
152.
а)
![]() ; б)
; б)![]() .
.
153.
а)
![]() ; б)
; б)![]() .
.
154.
а)
![]() ; б)
; б)![]() .
.
155.
а)
![]() ; б)
; б)![]() .
.
156.
а)
![]() ; б)
; б)![]() .
.
157.
а)
![]() ; б)
; б)![]() .
.
158.
а)
![]() ; б)
; б)![]() .
.
159.
а)
![]() ; б)
; б)![]() .
.
160.
а)
![]() ; б)
; б) .
.
2. Приложения дифференциального исчисления
191-200. Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить ее график.
191.
 . 192.
. 192. .
.
193.
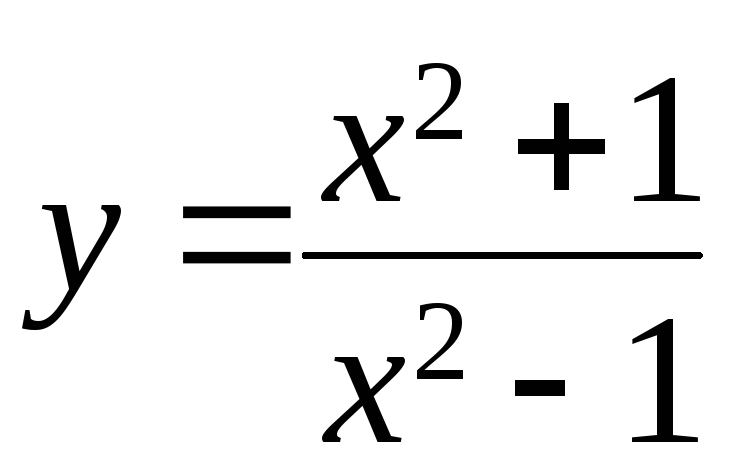 . 194.
. 194. .
.
195.
 . 196.
. 196.![]() .
.
197.
![]() . 198.
. 198. .
.
199.
 . 200.
. 200.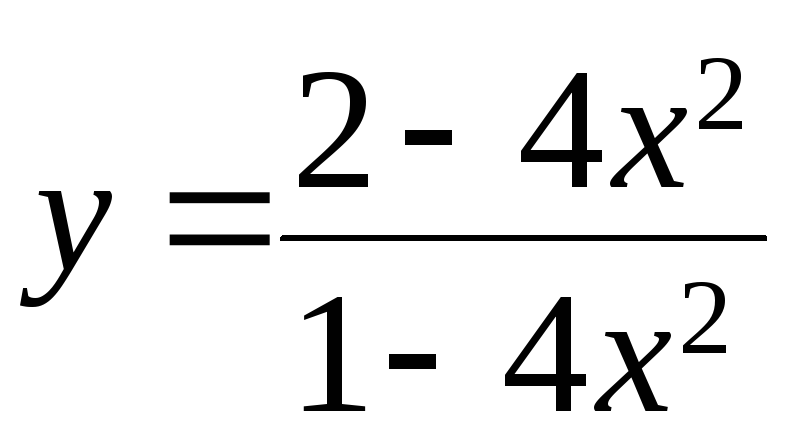 .
.
6. Дифференциальное исчисление функций нескольких переменных
231.
Дана функция
 .
.
Показать,
что
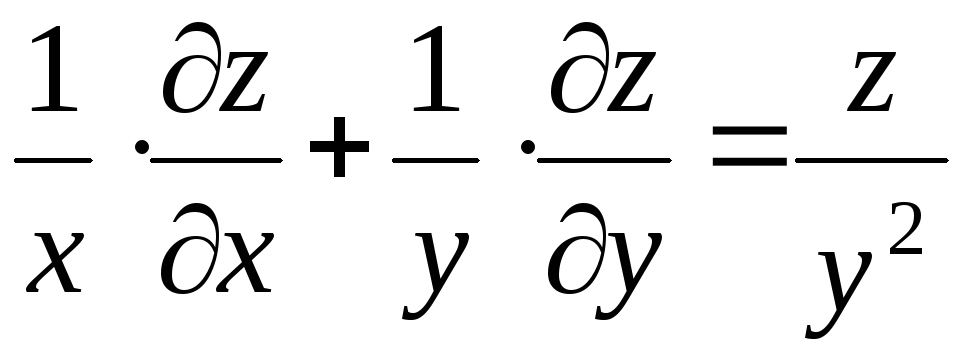 .
.
232.
Дана функция
 .
.
Показать,
что
 .
.
233.
Дана функция
![]() .
.
Показать,
что
 .
.
234.
Дана функция
![]() .
.
Показать,
что
 .
.
235.
Дана функция
![]() .
.
Показать,
что
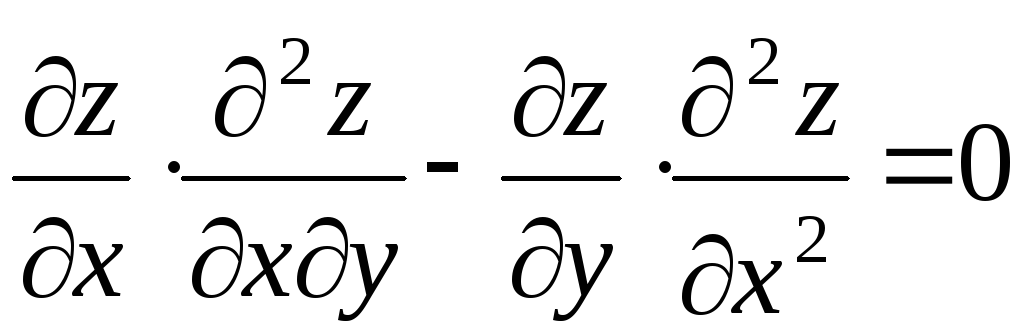 .
.
236.
Дана функция
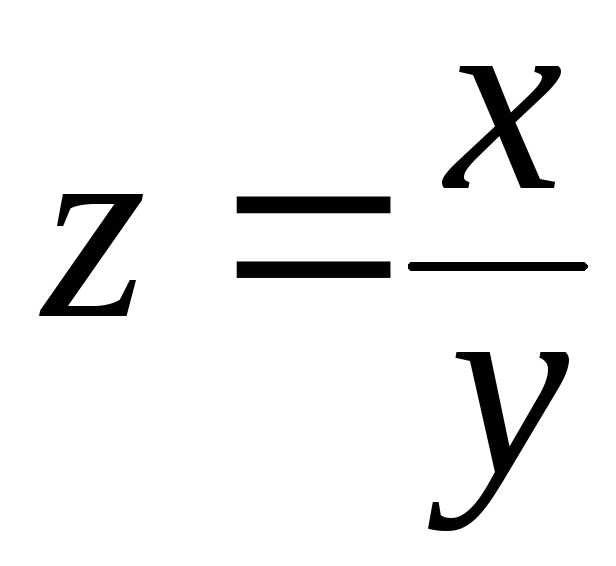 .
Показать, что
.
Показать, что .
.
.
237.
Дана функция
![]() .
.
Показать,
что
 .
.
238.
Дана функция
![]() .
.
Показать,
что
 .
.
239.
Дана функция
![]() .
.
Показать,
что
 .
.
240.
Дана функция
![]() .
.
Показать,
что
 .
.
251-260. Найти наименьшее и наибольшее значения функции z=f(x, y) в замкнутой области D, заданной системой неравенств. Сделать чертеж.
251. z=x2+y2-9xy+27; 0≤x≤3, 0≤y≤3.
252. z=x2+2y2+1; x≥0, y≥0, x+y≤3.
253. z=3-2x2 -xy-y2; x≤1, у≤х, у≥0.
254. z=x2+3y2+x-y; x≥1, y≥-1, х+y≤1.
255. z=x2+2xy +2y2; -1≤x≤1, 0≤y≤2.
256. z=5x2-3xy +y2+4; x≥-1, y≥-1, х+y≤1.
257. z=10+2xy -x2; 0≤y≤4- x2.
258. z=x2+2xy -y2+4 x; x≤0, y≤0, х+y+2≥0.
259. z=x2 +xy-2; 4 x2-4≤y≤0.
260. z=x2+xy; -1≤x≤1, 0≤y≤3.
261-270.
Дана функция
z=z(x,
y),
точка А(х0,
у0)
и вектор
![]() .
Найти: 1)
.
Найти: 1)![]() в точкеA;
2) производную в точке A
по направлению вектора
в точкеA;
2) производную в точке A
по направлению вектора
![]() .
.
261.
![]() .
.
262.
![]() .
.
263.
![]() .
.
264.
![]() .
.
265.
![]() .
.
266.
![]() .
.
267.
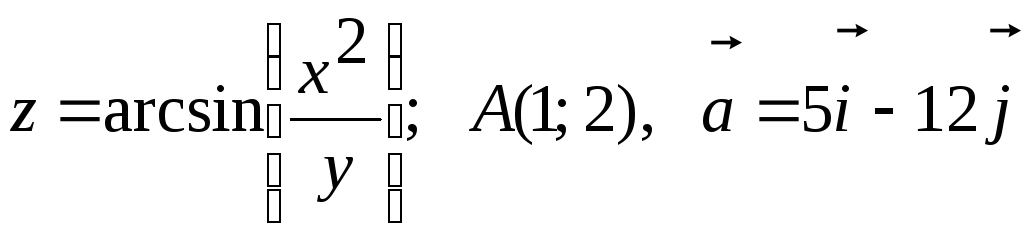 .
.
268.
![]() .
.
269.
![]() .
.
270.
![]() .
.
7. Неопределённый и определённыё интегралы
281-290. Найти неопределенные интегралы. В двух примерах (пункты а и б) проверить результаты дифференцированием.
281.
а)
![]() ; б)
; б)![]() ;
;
в)
 ; г)
; г) .
.
282.
а)
 ; б)
; б)![]() ;
;
в)
 ; г)
; г) .
.
283.
а)
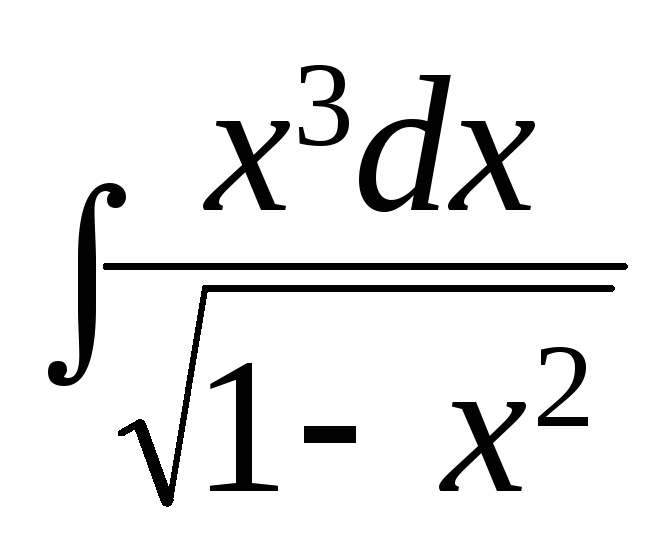 ; б)
; б)![]() ;
;
в)
 ;
г)
;
г)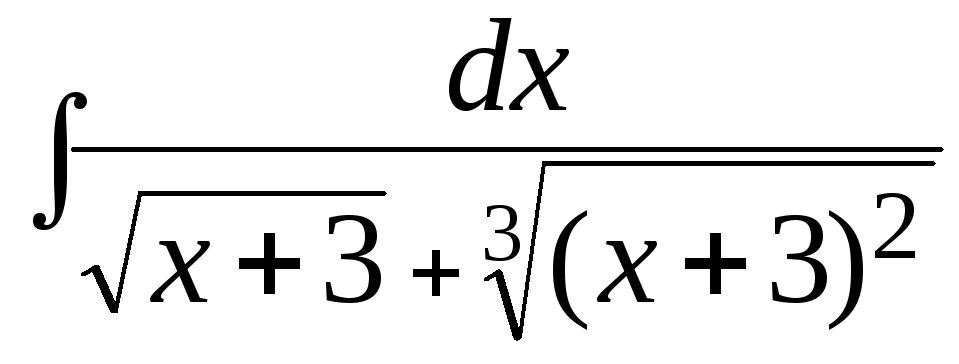 .
.
284.
а)
 ; б)
; б) ;
;
в)
 ; г)
; г)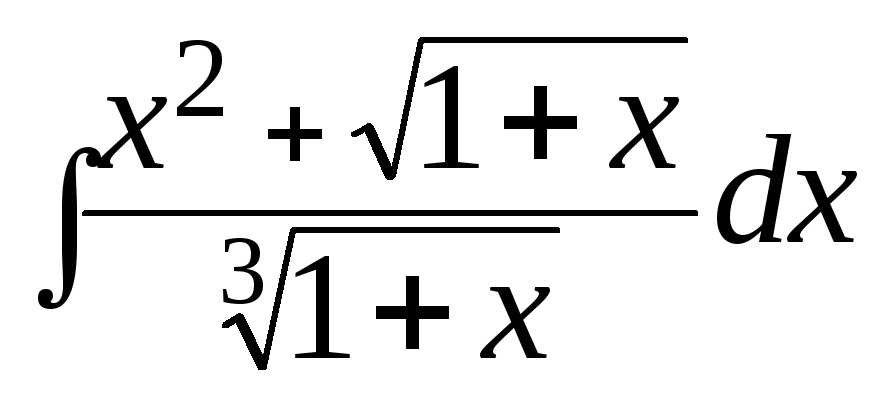 .
.
285.
а)
 ; б)
; б)![]() ;
;
в)
 ; г)
; г) .
.
286.
а)
 ; б)
; б) ;
;
в)
 ; г)
; г)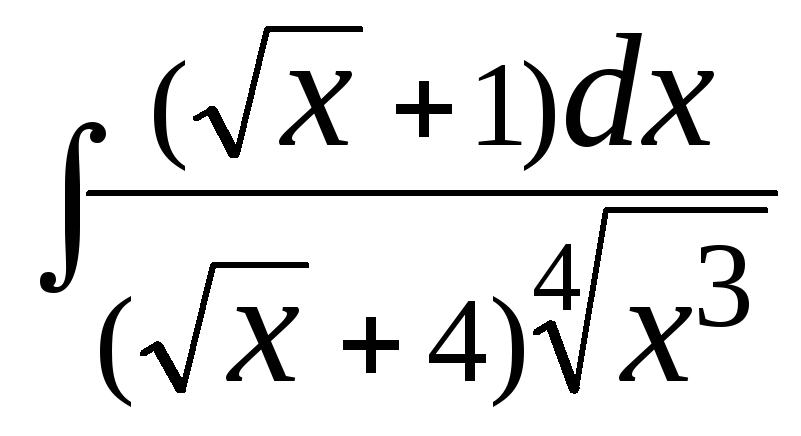 .
.
287.
а)
 ; б)
; б)![]() ;
;
в)
 ; г)
; г)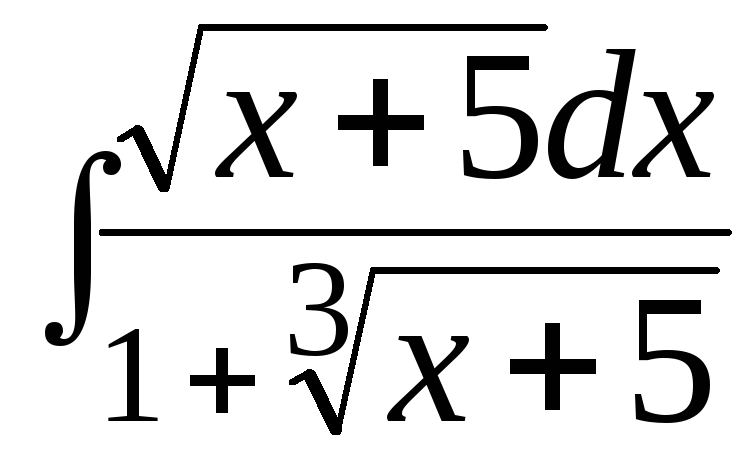 .
.
288.
а)
 ; б)
; б)![]() ;
;
в)
 ;
г)
;
г) .
.
289.
а)
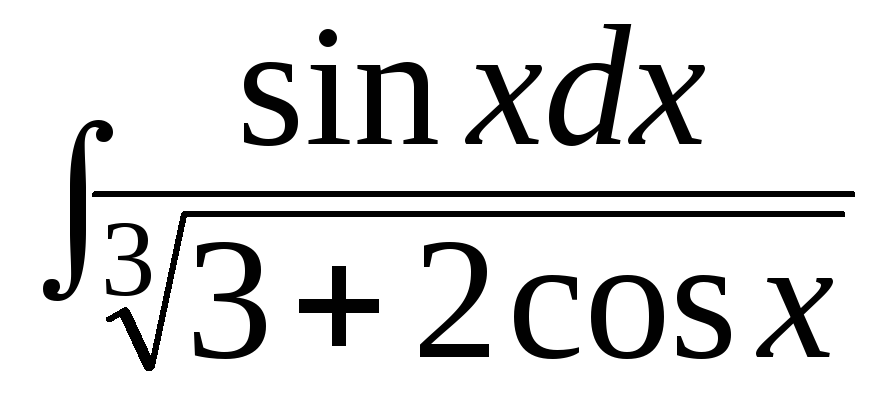 ; б)
; б)![]() ;
;
в)
 ;
г)
;
г) .
.
290.
а)
 ; б)
; б)![]() ;
;
в)
 ; г)
; г) .
.
301-310. Вычислить несобственный интеграл или доказать его расходимость.
301.
![]() .302.
.302.
 .
.
303.
 .304.
.304.
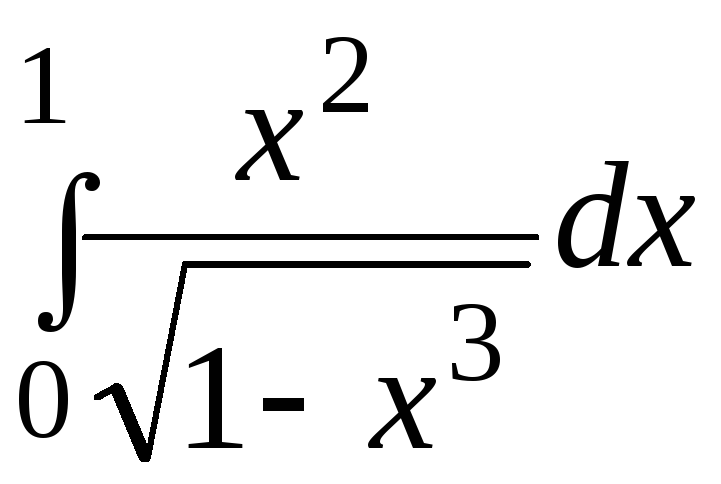 .
.
305.
 .306.
.306.
 .
.
307.
 .
.![]() 308.
308.
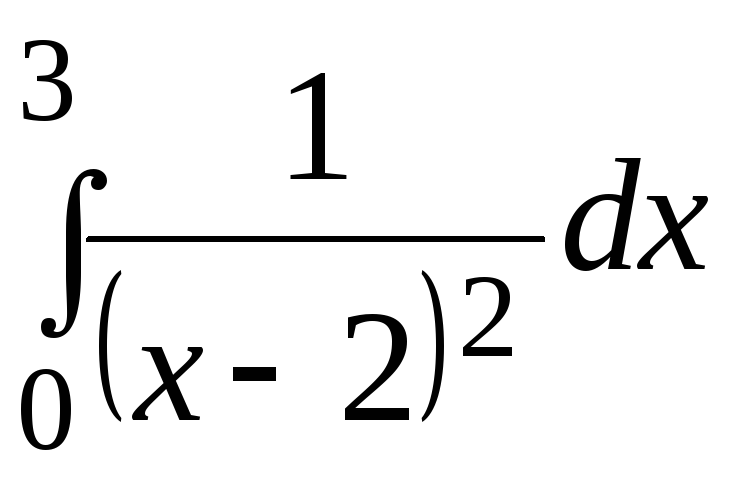 .
.
309.
 .
310.
.
310. .
.
8. Дифференциальные уравнения
321-330. Найти общее решение дифференциального уравнения.
321.
![]() .
322.
.
322.![]() .
.
323.
 .
324.
.
324.![]() .
.
325.
![]() .
326.
.
326.![]() .
.
327.
![]() .
328.
.
328.![]() .
.
329.
![]() . 330.
. 330.![]() .
.
341-350.
Найти частное решение дифференциального
уравнения
![]() ,
удовлетворяющее начальным условиям
,
удовлетворяющее начальным условиям![]() ,
,![]() .
.
341.
![]() ;
;![]() ,
,![]() .
.
342.
![]() ;
; ,
, .
.
343.
![]() ;
;![]() ,
,![]() .
.
344.
![]() ;
;![]() ,
,![]() .
.
345.
![]() ;
;![]() ,
,![]() .
.
346.
![]() ;
;![]() ,
,![]() .
.
347.
![]() ;
;![]() ,
,![]() .
.
348.
![]() ;
;![]() ,
,![]() .
.
349.
![]() ;
;![]() ,
,![]() .
.
350.
![]() ;
;![]() ,
,![]() .
.
