
Пу-112 КТэ 2 сем / Математика / собственные значения и собственные векторы
.docСобственные векторы и собственные
значения линейного оператора
Определение 1.
Собственным
вектором оператора
![]() называют
ненулевой вектор
называют
ненулевой вектор
![]() ,
удовлетворяющий равенству:
,
удовлетворяющий равенству:
![]() =
=![]() .
.
Определение 2.
Собственным
значением оператора
![]() называют
число
называют
число
![]() ,
для которого выполняется равенство:
,
для которого выполняется равенство:
![]() =
=![]() ,
где
,
где
![]() - ненулевой вектор.
- ненулевой вектор.
|
|
(1) |
|
|
(2) |
Решив последнее
уравнение относительно
![]() ,
найдем собственные значения матрицы.
Уравнение (5.8) называют характеристическим
уравнением матрицы
,
найдем собственные значения матрицы.
Уравнение (5.8) называют характеристическим
уравнением матрицы
![]() .
Найдя корни характеристического
уравнения, последовательно подставляя
их в систему (1) и решая получаемые
системы, найдем собственные векторы
матрицы
.
Найдя корни характеристического
уравнения, последовательно подставляя
их в систему (1) и решая получаемые
системы, найдем собственные векторы
матрицы
![]() ,
каждый из которых соответствует
определенному собственному значению.
,
каждый из которых соответствует
определенному собственному значению.
Рассмотрим несколько примеров, в каждом из которых будем выполнять последовательность действий решения задачи об отыскании собственных значений и собственных векторов матрицы.
Пример 1.
Найти собственные
значения и собственные векторы матрицы
![]() .
Дать геометрическую интерпретацию
полученного решения.
.
Дать геометрическую интерпретацию
полученного решения.
Решение
-
Матрица имеет размерность 2
 2,
то есть является представлением
линейного оператора в пространстве
2,
то есть является представлением
линейного оператора в пространстве
 .
Собственный вектор матрицы будем искать
в виде:
.
Собственный вектор матрицы будем искать
в виде:
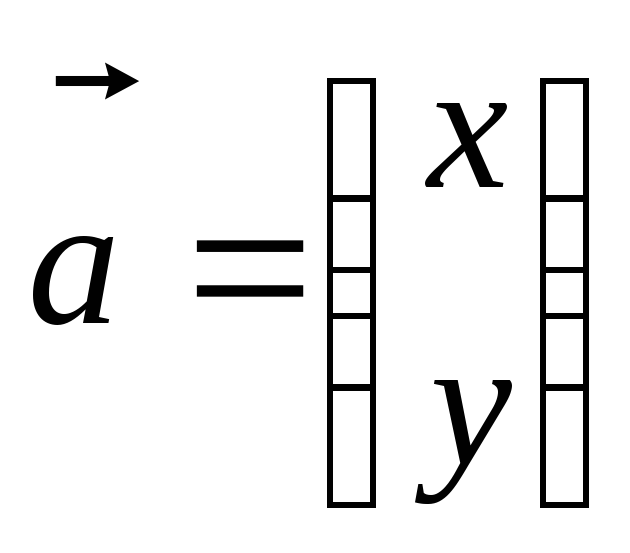 .
. -
Составим уравнение для отыскания собственных векторов в матричном виде:
![]()
![]()
![]()
![]()
![]()
3. Перепишем матричное уравнение в виде системы уравнений:
![]()
-
Однородная система имеет ненулевые решения тогда и только тогда, когда определитель ее главной матрицы равен 0. Получаем характеристическое уравнение системы и решаем его:
![]()
![]()
![]()
![]() .
.
Собственные
значения матрицы
![]() :
:
![]() ,
,
![]() .
.
-
Найдем собственные векторы для каждого собственного значения:
|
Пусть
|
Пусть
|
П ример
2. Найти собственные значения и
собственные векторы линейного оператора
, заданного в некотором базисе матрицей
А=
ример
2. Найти собственные значения и
собственные векторы линейного оператора
, заданного в некотором базисе матрицей
А=![]() .
.
-
Составим и решим характеристическое уравнение
 .
.
В нашей задаче
![]() .
.
Тогда характеристическое уравнение принимает вид:
![]() ,
или
,
или
![]() ,
,
![]() ,
,
![]() ,
,
![]() - собственные
значения линейного оператора.
- собственные
значения линейного оператора.
-
Найдем собственные векторы, соответствующие собственному значению
 ,
решая матричное уравнение:
,
решая матричное уравнение:
![]() х=0
или
х=0
или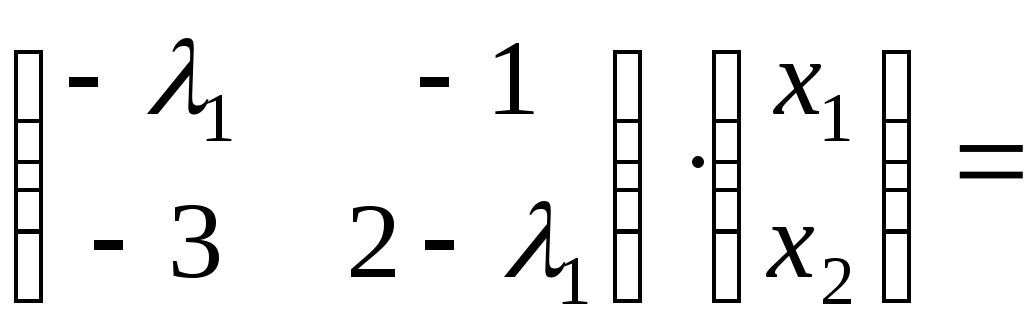
 ,
т.е.
,
т.е.

![]()
![]() .
.
Полагая в последнем
равенстве
![]() ,
получим
,
получим
![]() .
.
Откуда собственные
векторы, соответствующие собственному
значению
![]() ,
имеют вид х1=
,
имеют вид х1=![]() .
.
-
Найдем собственные векторы, соответствующие собственному значению
 ,
решая матричное уравнение:
,
решая матричное уравнение:
![]() х=0
или
х=0
или
 ,
т.е.
,
т.е.

![]() .
.
Полагая в последнем
равенстве
![]() ,
получим
,
получим
![]() .
.
Откуда собственные
векторы, соответствующие собственному
значению
![]() ,
имеют вид х2=
,
имеют вид х2=![]() .
.
Ответ. Собственному
значению![]() соответствуют собственные векторы
х1=
соответствуют собственные векторы
х1=![]() ,
а собственному значению
,
а собственному значению![]() собственные векторы
собственные векторы
х 2=
2=![]() .
.
П ример
3. Найти собственные значения и
собственные векторы линейного оператора
, заданного в некотором базисе матрицей
А=
ример
3. Найти собственные значения и
собственные векторы линейного оператора
, заданного в некотором базисе матрицей
А=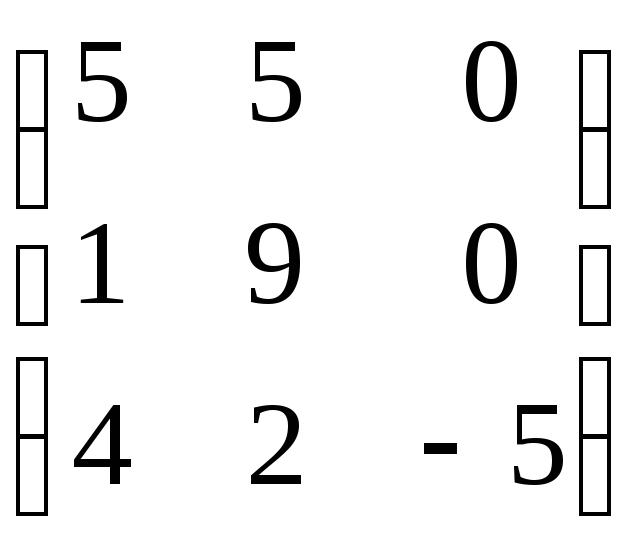 .
.
-
Найдем собственные значения линейного оператора. Для этого составим характеристическое уравнение и найдем его корни:
 .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() - собственные значения линейного
оператора.
- собственные значения линейного
оператора.
-
Найдем собственные векторы, соответствующие собственному значению
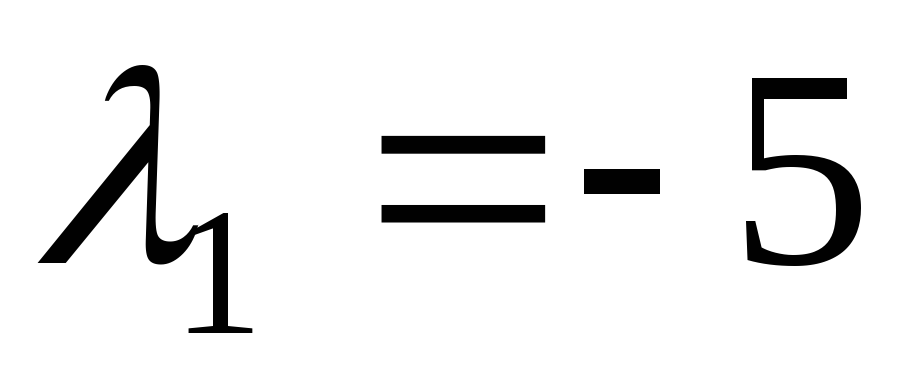 .
Исходя из соотношения
.
Исходя из соотношения
 х=0
или в нашем случае
х=0
или в нашем случае
 ,
запишем систему:
,
запишем систему:
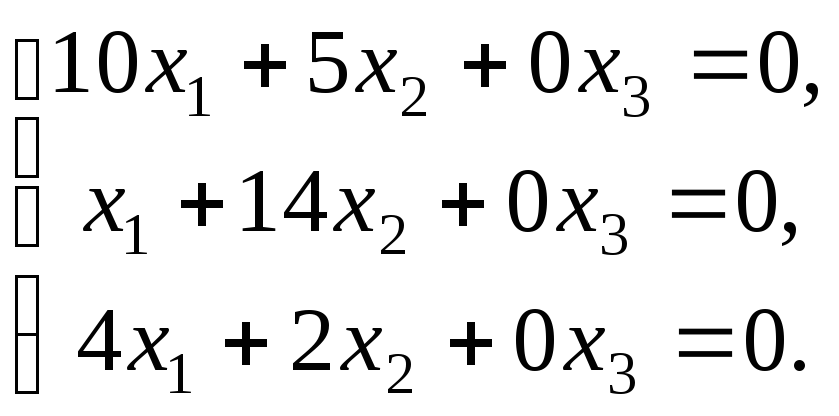 Решая методом
Гаусса, получаем
Решая методом
Гаусса, получаем

Поскольку ранг
матрицы системы (r=2)
меньше количества неизвестных, то
система имеет бесконечное множество
решений. Записывая преобразованную
систему и решая ее, получим
![]() ,
,
![]() .
.
Таким образом,
собственные векторы, соответствующие
собственному значению
![]() ,
имеют вид: Х1=
,
имеют вид: Х1=![]() .
.
-
Найдем собственные векторы, соответствующие собственному значению
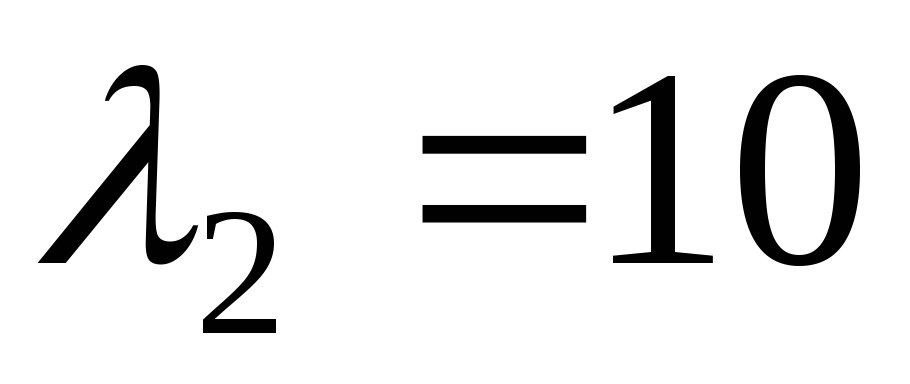 .
Исходя из соотношения
.
Исходя из соотношения
 х=0
или в нашем случае
х=0
или в нашем случае
 ,
т.е.
,
т.е.
 Решая методом
Гаусса, получаем
Решая методом
Гаусса, получаем

откуда, система
принимает вид

Полагая
![]() ,
получим
,
получим
![]() .
.
Таким образом,
собственные векторы, соответствующие
собственному значению
![]() ,
имеют вид: Х2=
,
имеют вид: Х2= .
.
-
Найдем собственные векторы, соответствующие собственному значению
 .
Исходя из соотношения
.
Исходя из соотношения
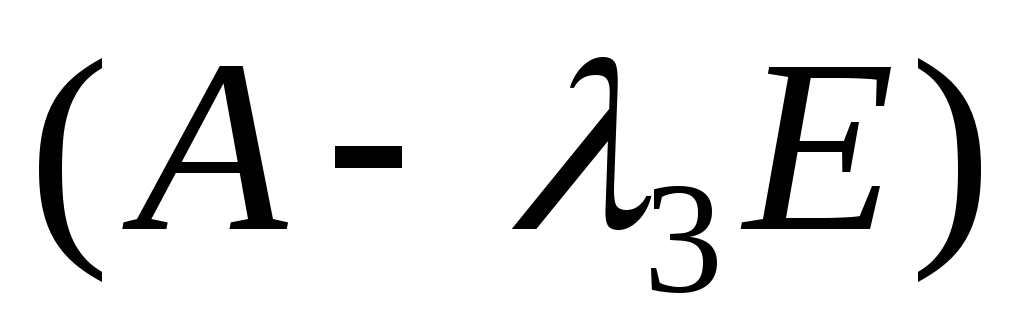 х=0
или в нашем случае
х=0
или в нашем случае
 ,
т.е.
,
т.е.
 Решая методом
Гаусса, получаем
Решая методом
Гаусса, получаем
 ,
,
откуда, система
принимает вид

Полагая
![]() ,
получим
,
получим
![]() .
.
Т аким
образом, собственные векторы,
соответствующие собственному значению
аким
образом, собственные векторы,
соответствующие собственному значению
![]() ,
имеют вид: Х3=
,
имеют вид: Х3= .
.

