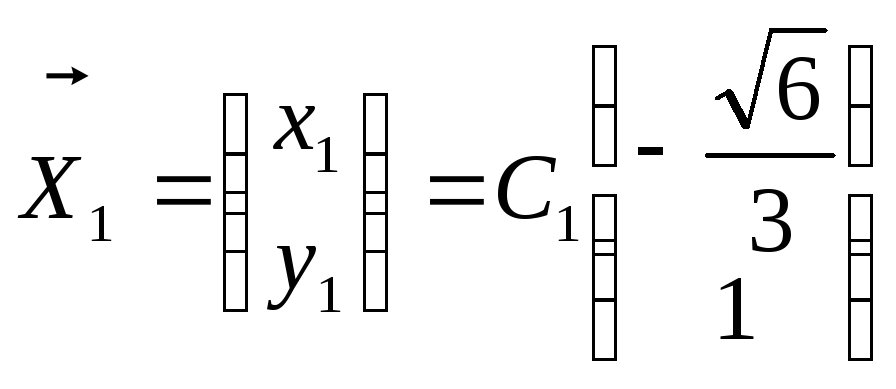7.3. Кривые второго порядка на плоскости

Определение 1. Кривая второго порядка на плоскости – это линия, уравнение которой в заданной системе координат имеет вид:

,

(7.5)

где ,,,,,- числовые коэффициенты, причем хотя бы одно из чисел,илине равно нулю.

Уравнение (7.5) содержит две части:

линейная часть =

квадратичная форма =

Будем предполагать, что система координат, в которой рассматриваем кривую, это декартова прямоугольная система, то есть репер с ортонормированным базисом . В общем случае построить кривую по уравнению (7. ) довольно трудно. Но всегда можно перейти к другому ортонормированному реперу, в котором легко установить вид кривой, а затем и построить ее. Процедура перехода к другому реперу выполняется за 2 шага:

Шаг 1. Привести квадратичную форму =к главным осям.

• Матрица квадратичной формы: .

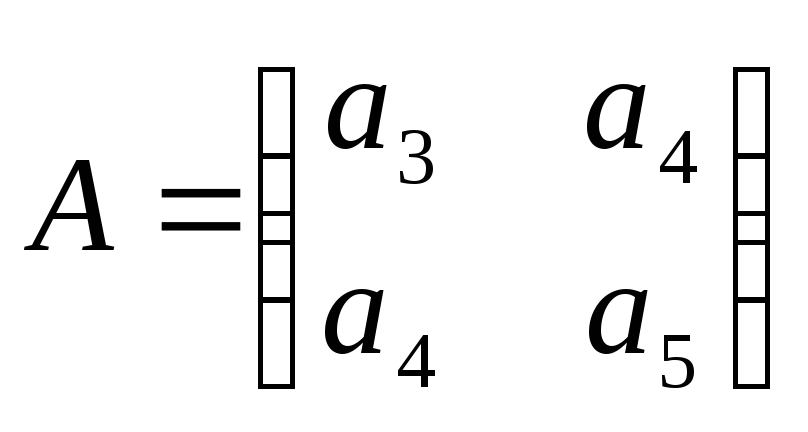• Характеристическое уравнение:

.

• Собственные значения матрицы :

.

• Собственные направления матрицы :

.

Последнее равенство требует, чтобы , то есть. Последнее условие нарушено, если

=.

Таким образом, если , то квадратичная форма приведена к главным осям и дальнейших ее преобразований не требуется.

• Ортонормированный базис собственных векторов: ().

• Матрица перехода от базиса () к базису ():.

• Преобразование координат «старого» базиса: .

• Матрица квадратичной формы в базисе ():.

• Вид квадратичной формы в базисе ():.

• Вид линейной формы в базисе ():

==

= =

• Вид уравнения кривой второго порядка в базисе ():

Шаг 2. Не меняя базиса (), перейдем к новому началу координат, координаты которого в «старом» репере (). Целью этого перехода является получение уравнения кривой, в котором коэффициенты при линейных слагаемых равны нулю. Сразу оговоримся, что такую процедуру можно выполнить не всегда. Пользуясь формулами (7. стр. ), имеем:

.

Раскрывая скобки и группируя линейные и квадратичные слагаемые, получаем:

+.

Приравняем коэффициенты при линейных слагаемых к нулю и из полученных равенств найдем :

.

Последние равенства выполнимы, если и. При выполнении этих условий, уравнение кривой принимает вид:

, (7. )

где .

Если же или, то уравнение кривой в базисе () имеет вид:

или .

(7.6)

Преобразуем первое из уравнений (7. ). выберем так, чтобы свободный член уравнения и коэффициент пристали равными нулю:

.

(7.7)

.

После этих преобразований уравнение (7.6) принимает вид:

,

где .

Второе уравнение (7.6) аналогичными преобразованиями приводим к виду:

,

где .

Вывод. Существует система координат с ортонормированным базисом, в котором уравнение кривой второго порядка имеет одну из следующих форм:

,

где ,,,- любые действительные числа. Такую систему координат называютканонической системой координат кривой второго порядка, а ее уравнение в этой системе – каноническим уравнением кривой второго порядка.

Геометрическими образами уравнения являются следующие линии:

1. Пустая линия. . Если, то равенствоневыполнимо при любых значенияхи.

2. Точка. ,иимеют одинаковые знаки, например,. Равенствовыполнимо лишь в точке.

3. Пара пресекающихся прямых. 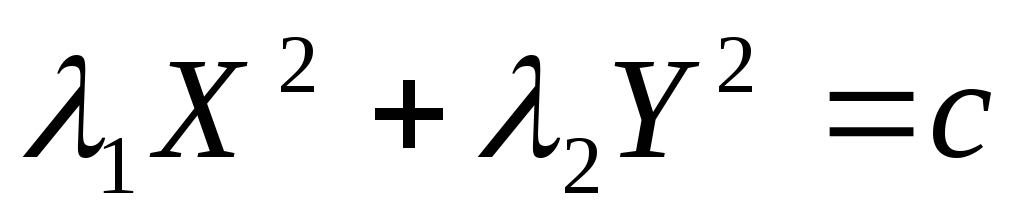,иимеют разные знаки, например,. Равенствораспадается на два равенства:, каждое из которых определяет прямую, проходящую через начало координат.

4. Пара параллельных прямых и пара совпадающих прямых. ,- уравнение двух прямых, параллельных вектору, если,- уравнение пары совпадающих прямых.

5. Эллипс. ,,.

6. Гипербола. 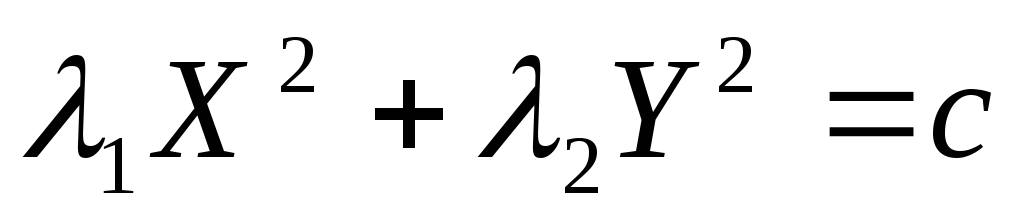,,. Аналогично.

7. Уравнения ,,определяютпараболу.

Пример. Определить тип линии, заданной уравнением:

.

Решение

Задание будем выполнять по действиям.

Выделим в уравнении линии линейную часть и квадратичную форму:

.

Приведем квадратичную форму к главным осям:

• Матрица квадратичной формы: .

• Составим и решим характеристическое уравнение:

, .

• Найдем собственные направления матрицы:

• Проверим ортогональность векторов и:

=.

• Нормируем векторы и:

; .

; .

• Матрица перехода от базиса к базисуи преобразование координат:

;

Вид квадратичной формы в базисе :

.

Вид линейной части в базисе :

=

.

Вид уравнения кривой в базисе :

+=0.

2. Перенесем начало координат в точку так, чтобы исчезли линейные слагаемые:

+=0

=0

.

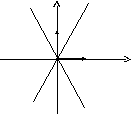
Ответ: В репере уравнение имеет вид:Уравнение определяет пару пересекающихся прямых:и.

Рассмотрим наиболее важные кривые второго порядка – эллипс, гиперболу и параболу.

- -	Эллипсом называют плоскую замкнутую кривую, сумма расстояний от каждой точки которой до двух фиксированных точек –фокусов эллипса, есть величина постоянная, равная . Характеристики эллипса: Фокальное расстояние . Большая ось =. Малая ось 2.

• Эксцентриситет .

Эксцентриситет характеризует степень вытянутости эллипса: , чем больше, тем «уже» эллипс. В предельных случаях: (а)эллипс становится окружностью, (б)эллипс вырождается в двойной отрезок.

Каноническая система координат – система, оси которой совпадают с осями симметрии эллипса. Уравнения эллипса в канонической системе координат: (а) - большая ось совпадает с осью, (б)- большая ось совпадает с осью.

- -	Гиперболой называют плоскую кривую, модуль разности расстояний от каждой точки которой до двух фиксированных точек –фокусов гиперболы, есть величина постоянная, равная . Характеристики эллипса: Фокальное расстояние . Действительная ось =. Мнимая полуось .

• Эксцентриситет .

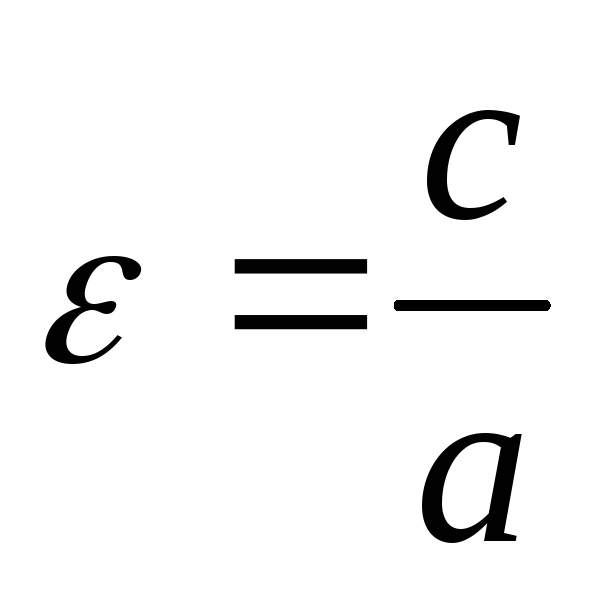• Асимптоты гиперболы: прямые , к которым приближается гипербола на бесконечности.

Эксцентриситет характеризует степень «раскрытости» гиперболы: , чем больше, тем более раскрыта гипербола.

Каноническая система координат – система, оси которой совпадают с осями симметрии гиперболы. Уравнения эллипса в канонической системе координат: (а) - действительная ось совпадает с осью, (б)- действительная ось совпадает с осью.

Параболой называют плоскую кривую, расстояние от каждой точкикоторой до фиксированной точки–фокуса параболы, равно расстоянию от этой точки до фиксированной прямой –директрисы параболы. Парабола характеризуется расстоянием между фокусом и директрисой. Числоназываютпараметром параболы. Одна из осей канонической системы координат проходит через фокус параболы, перпендикулярно директрисе, вторая – является осью симметрии параболы

.

Канонические уравнения параболы:

1. , . Ось симметрии совпадает с осью , ветви параболы направлены вправо.

2. , . Ось симметрии совпадает с осью , ветви параболы направлены влево.

3. , . Ось симметрии совпадает с осью , ветви параболы направлены вверх.

4. , . Ось симметрии совпадает с осью , ветви параболы направлены вниз.