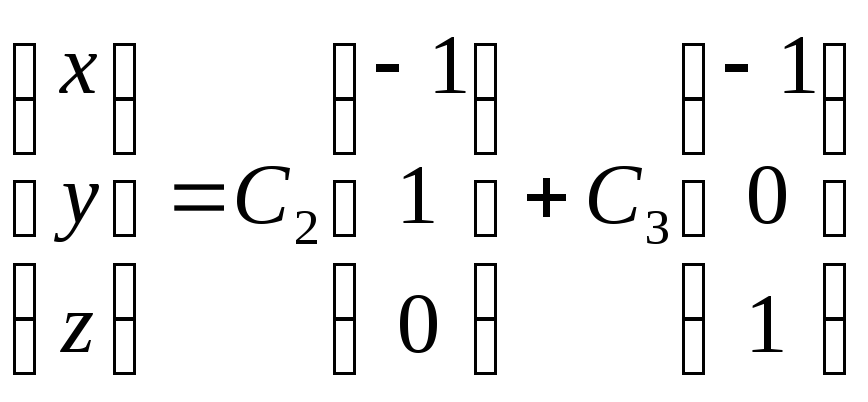7. Кривые и поверхности второго порядка

7.1. Линейное пространство с ортонормированным базисом

При изучении геометрических объектов с использованием системы координат наиболее удобным оказывается ортонормированный базис векторы которого имеют единичную длину и попарно перпендикулярны друг другу. Это обстоятельство требует выделения линейных пространств с ортонормированными базисами в отдельный класс пространств, что привело к созданию теории евклидовых пространств. Ознакомимся с некоторыми положениями этой теории.

Определение 1. Евклидовым пространством называют линейное пространство L над полем действительных чисел , в котором определена операция скалярного умножения, то есть правило, по которому каждой паре векторов,ставится в соответствие определенное (единственное) число, так, что выполнены четыре аксиомы:

1. Коммутативность: для любых .

2. Дистрибутивность относительно сложения:

для любых .

3. Однородность: для любых .

4. Неотрицательность квадрата: для любого .

Как было неоднократно отмечено, в пространстве скалярное произведение векторов вычисляют по правилу:

,

=.

В евклидовом пространстве определены длины векторов и углы между векторами:

, =.

Если вектор имеет единичную длину, его называют нормированным вектором. Если для векторов ,выполняется равенство=0, то векторы,называютортогональными векторами.

Определение 2. Систему векторов -мерного евклидова пространстваназываютортонормированной системой векторов, если каждый из ее векторов имеет единичную длину и все векторы попарно ортогональны. Если базис пространства является ортонормированной системой векторов, его называют ортонормированным базисом.

Справедлива теорема:

Теорема об ортонормированных системах. Пусть - евклидово пространство. Тогда:

1. Любая ортонормированная система векторов пространства свободна.

2. Матрица перехода от одного ортонормированного базиса к другому удовлетворяет равенству:. (Чтобы найти матрицу, обратную матрице перехода, достаточно транспонировать матрицу).

Справедливость второго утверждения мы видели на примере раздела 6.4 (см. стр. ).

Определение 3. Матрицу , для которой выполняется равенство:, называютортогональной матрицей.

Определение 4. Линейный оператор евклидова пространства называют симметрическим или самосопряженным оператором, если для любых векторов иэтого пространства выполняется равенство:.

В дальнейшем потребуются следующие свойства симметрических операторов:

1. Линейный оператор является симметрическим тогда и только тогда, когда в любом ортонормированном базисе пространства его матрица является симметрической, то есть выполняется равенство: .

2. Все собственные значения симметрического оператора являются действительными числами.

3. Собственные векторы симметрического оператора, соответствующие различным собственным значениям ортогональны.

4. Для любого симметрического оператора существует ортонормированный базис пространства, состоящий из собственных векторов пространства.

7.2. Квадратичные формы и их приведение к главным осям

Определение 1. Пусть --мерное евклидово пространство,- его базис (не обязательно ортонормированный),переменный вектор. Квадратичной формой в пространственазывают однородный многочлен с действительными коэффициентами от координат переменного вектора, то есть выражение:

(7.1)

Рассмотрим несколько примеров квадратичных форм в пространствах и.

Примеры.

1. ; ,.

Запишем коэффициенты квадратичной формы в виде матрицы: .

2. . Матрица коэффициентов имеет вид:

.

3. ;

.

Коэффициенты квадратичной формы можно записать в виде матрицы квадратичной формы:

.

Как видно из примеров, матрица квадратичной формы симметрична, относительно главной диагонали.

Используя матрицу, квадратичную форму можно записать более кратко:

=.

(7.2)

Смена базиса пространства приведет к изменению матрицы квадратичной формы. Рассмотрим, как изменится матрица при замене базиса на базис. Пустьи- столбцы координаты вектора, аи- матрицы квадратичной формы в этих базисах.

, - матричная запись квадратичной формы в базисахисоответственно.

Пусть также матрица перехода от базисак базису, а-матрица обратного перехода, то есть,. Для любой матрицы справедливо равенство,, которое проверяется элементарно. С учетом этого равенства имеем:

===.

Следовательно:

(7.3)

Поскольку =, а для ортонормированных базисов=, можно сократить обозначения:=,=,. С учетом этих равенств, для ортонормированных базисовиимеем:

,

(7.4)

где - матрица перехода от базисак базису, столбцами которой являются координаты базисных векторовв базисе,иматрицы квадратичной формы в этих базисах.

Справедлива теорема:

Теорема Лагранжа. Для всякой квадратичной формы существует замена переменных, переводящая эту форму в сумму квадратов.

В аналитической геометрии нахождение базиса, в котором квадратичная форма превращается в сумму квадратов, называют приведением квадратичной формы к главным осям.

Пример. Привести квадратичную форму , к главным осям.

Эта задача достаточно сложна и распадается на ряд самостоятельных задач.

Задача 1

Запишем матрицу квадратичной формы.

Задача 2.

Составим характеристическое уравнение и решим его.

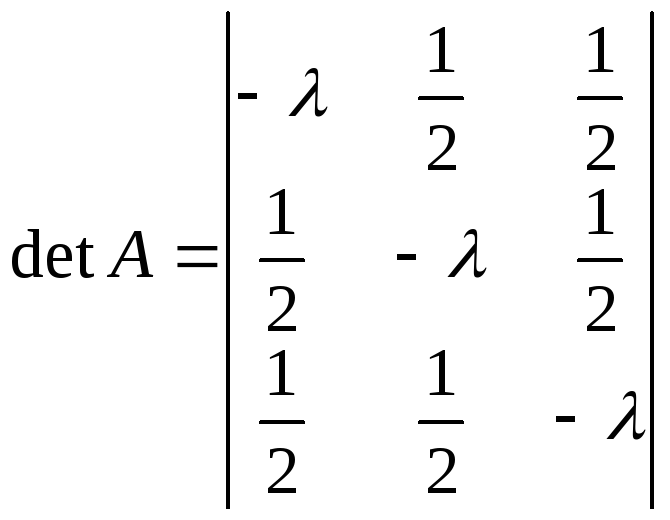= 0

Задача 3.

Для каждого собственного значения найдем собственные направления матрицы

, , , =

, , =

Собственные направления матрицы :

,, ().

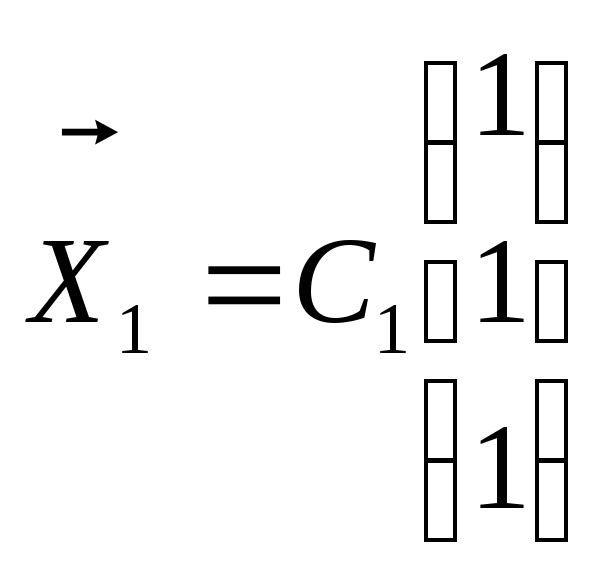при любых значениях , как собственные векторы симметрической матрицы, соответствующие различным собственным значениям. Собственное направление- это множество всех линейных комбинаций двух линейно независимых векторов

и ,то есть линейное двумерное пространство-плоскость.

Задача 4

Выберем ортонормированный базис, состоящий из собственных векторов матрицы .

Для этого:

• Ортогонализируем систему векторов , то есть выберем из множества собственных векторов три взаимно перпендикулярных вектора. Для этого выполним последовательность операций:

1. В качестве первого базисного вектора можно взять любой из векторов направления :

.

2. В качестве второго вектора возьмем любой из векторов плоскости , например,

.

3. Пусть . Подберемитак, чтобы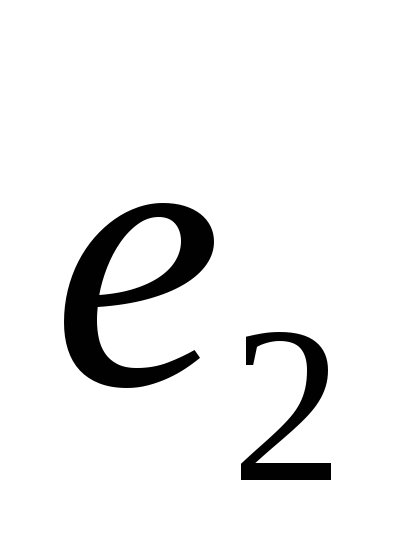ибыли ортогональны:

==0,

- два решения полученного уравнения. Первое решение обращаетв нуль, следовательно, является посторонним.

4. Выбираем второе решение: , при которомпринимает вид:

==.

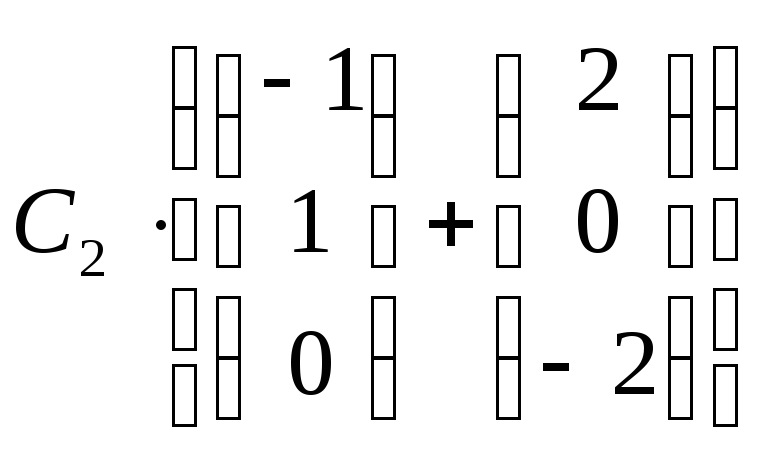5. Проверим ортогональность векторов и: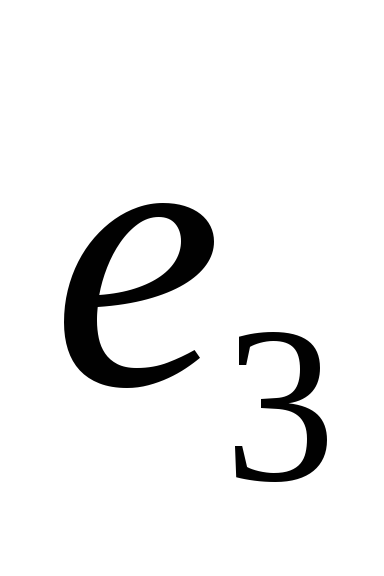

при любых значениях .

• Нормируем ортогональную систему векторов (), то есть выберемитак, чтобы длины векторов равнялись единице.

1 ;

1 ;

1 .

Знаки «+» или « - « перед позволяют сделать тройку (,,) правой или левой тройкой векторов. Смешанное произведение этих векторов:

=-.

Если (-)>0, то тройка векторов правая, если (-)<0, - то левая.

Выберем правый базис, положив ,,.

Запишем результаты вычислений.

1. Собственные значения матрицы :

2.Собственные векторы матрицы , образующие правый ортонормированный базис – векторы,,.

3. Координаты «новых» базисных векторов ,,в «старом» базисе:

, ,.

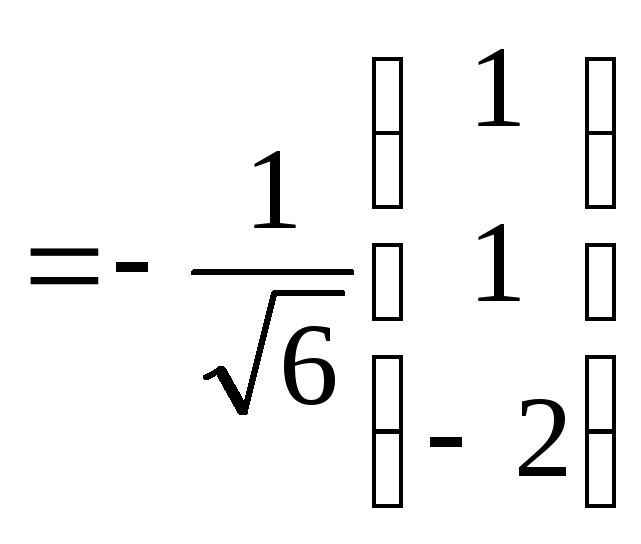4. Матрица перехода от к:

.

5. Преобразование координат при переходе от к:

.

6. Матрица перехода от к:

.

7. Преобразование координат при переходе от к:

.

8. Матрица квадратичной формы в базисе:

.

9. Матрица квадратичной формы в базисе:

.

10. Вид квадратичной формы в базисе:

=.

Алгоритм приведения квадратичной формы к главным осям.

1. Записать матрицу квадратичной формы.

2. Составить характеристическое уравнение и решить его.

3. Найти собственные направления матрицы для каждого собственного значения.

4. Из множества собственных направлений выбрать систему ортонормированных векторов.

5. Записать матрицу квадратичной формы и квадратичную форму в ортонормированном базисе собственных векторов матрицы.

6. Записать матрицы перехода от «старого» базиса к «новому» и от «нового» к «старому».
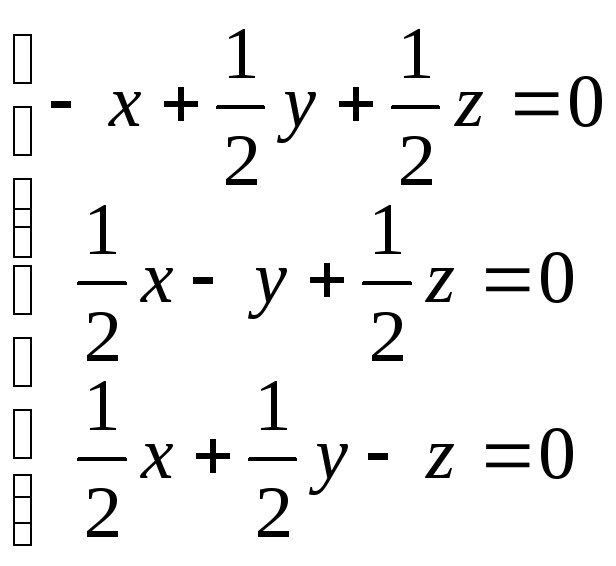
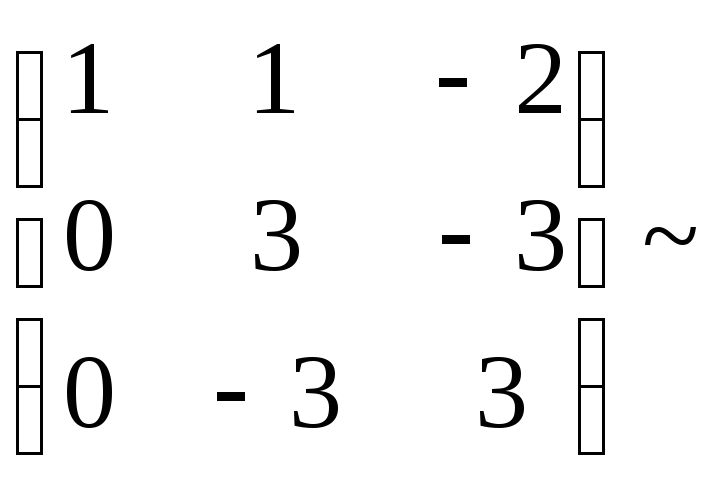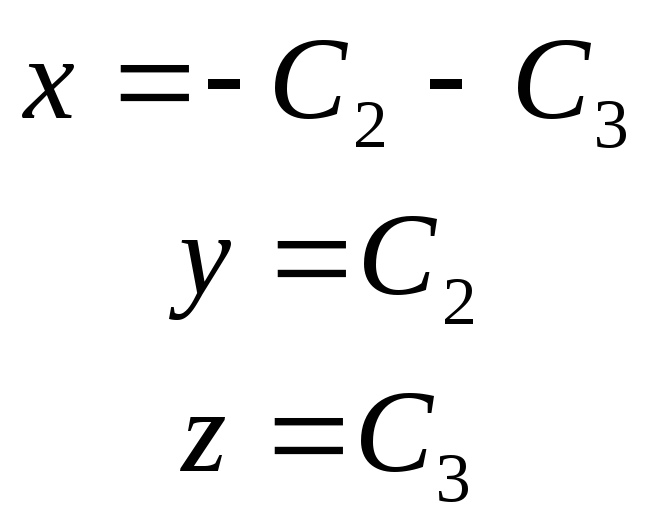