
- •Задания к контрольной работе по дисциплине
- •1. Элементы линейной алгебры и аналитической геометрии
- •2. Производная и её приложение
- •3. Приложения дифференциального исчисления
- •4. Дифференциальное исчисление функций нескольких переменных
- •5. Неопределённый и определённыё интегралы
- •6. Дифференциальные уравнения
- •7. Двойные и криволинейные интегралы
- •8. Ряды
- •11 – 20.
- •51 – 60.
- •91 – 100.
- •111 – 120.
- •151 – 160.
- •191 – 200 .
- •231-240.
- •251-260.
- •281 – 290.
- •301– 310
- •321 – 330
- •461 – 470 .
- •Задания для выполнения контрольной работы по дисциплине
231-240.
Показать,
что функция
![]() удовлетворяет равенству:
удовлетворяет равенству:

Находим
частные производные по
![]() и по
и по![]() :
:
![]()
![]()
 Подставим
в равенство частные производные.
Подставим
в равенство частные производные.

 ;
;
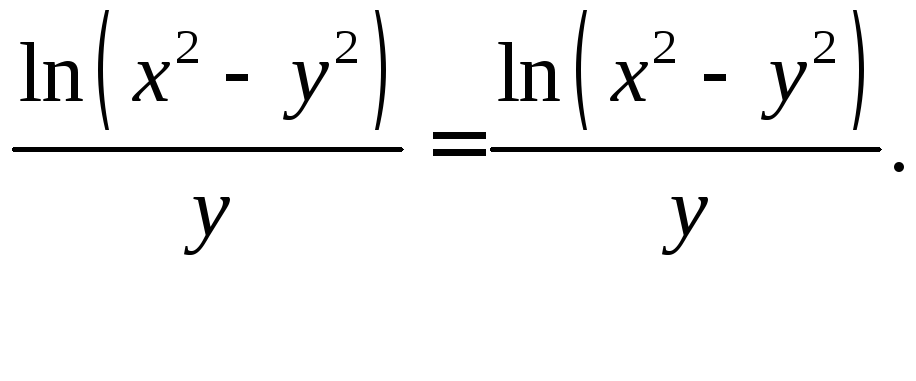
Равенство верно.
251-260.
Найти
наименьшее и наибольшее значения
функции
![]()
в области
![]()

y








 В
С
В
С
3
D
2
А D
0 1 2 x
а) Найдём стационарные точки

Точка
![]() - стационарная, но не принадлежит областиD.
- стационарная, но не принадлежит областиD.
б) Исследуем данную функцию на границах квадрата АВСD
АВ:
![]()
Функция
возрастает на границе АВ
![]()
ВС:![]()
![]()
На
границе ВС
функция
возрастает
![]()
![]()
Значит
на границе
![]() фнкция возрастает
фнкция возрастает![]()
![]()

Значит
на границе
![]() фнкция возрастает
фнкция возрастает![]()
Найденные значения z сравним и выделяем

261 – 270
Дана
функция
![]() точка
точка![]() и вектор
и вектор![]()
![]() Найти
Найти
![]() в
точке
в
точке![]() и производную в точке
и производную в точке![]() по направлению вектора
по направлению вектора![]() .
.
![]()
Найдём
частные производные и вычислим их
значение в точке
![]() .
.![]()


![]() –направляющие
косинусы вектора
–направляющие
косинусы вектора
![]()

Литература к заданиям 231 – 240, 251 – 260 , 261 – 270 – П.Е.Данко , А.Г.Попов, Т.Я.Кожевникова Высшая математика в упражнениях и задачах
гл.
VIII
§§1-2, §4.![]()
281 – 290.
Найти неопределённые интегралы, выполнив проверку дифференцированием в первых двух примерах.

Решение

Проверка:
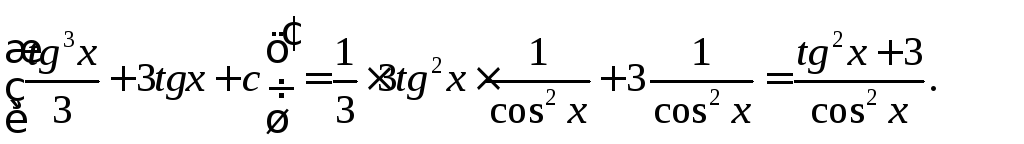
![]()
Метод
интегрирования по частям для функции
![]()
Формула:
![]()

Проверка:


Найдём коэффициенты


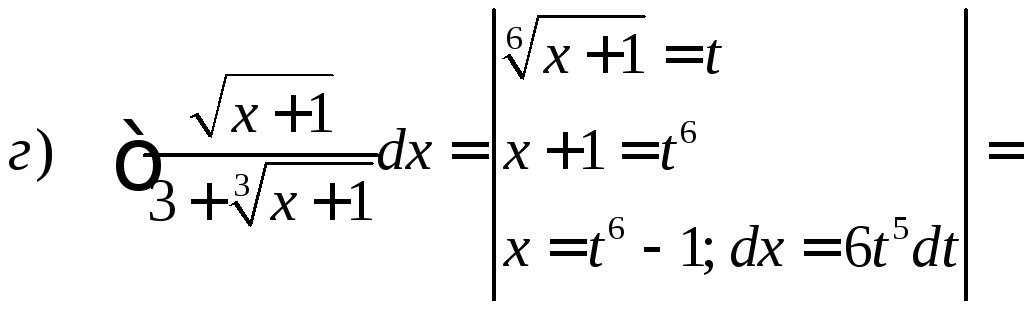
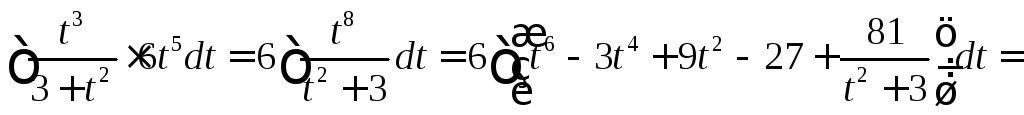


301– 310
Вычислить несобственный интеграл

Несобственный интеграл расходится.
Методы интегрирования рассматриваются в учебном пособии
– П.Е.Данко , А.Г.Попов, Т.Я.Кожевникова Высшая математика в упражнениях и задачах ч. I, гл. IХ. §§1-4.
В данном задании предлагается решить дифференциальное уравнение одного из трёх типов – однородное, линейное или с разделяющимися переменными. Предлагается решение однородного уравнения
321 – 330
В данном задании предлагается решить дифференциальное уравнение одного из трёх типов – однородное, линейное или с разделяющимися переменными. Предлагается решение однородного уравнения
Найти общее решение дифференциального уравнения первого порядка.
![]()
![]() .
.
Уравнение является однородным.
Функции
![]()
![]() однородные второго порядка.
однородные второго порядка.
Уравнение можно привести к виду
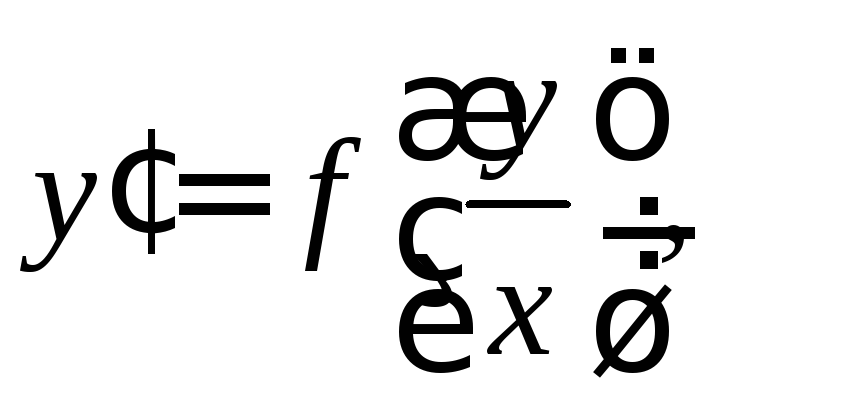 разделить
обе части на
разделить
обе части на
![]() а затем на
а затем на![]() .
.

Введём подстановку

Разделяем переменные:

Интегрируем обе части,получаем
![]()
Общее решение примет вид

Задание 341-350.
Найти общее и частное решения дифференциального уравнения
![]() при
начальных условиях
при
начальных условиях
![]() .
.
Однородное уравнение
![]() имеет
характеристическое уравнение
имеет
характеристическое уравнение
![]()
корни
которого
![]() .
.
Тогда
общее решение
![]()
- для однородного уравнения
Согласно
теории общее решение данного неоднородного
уравнения имеет вид
![]() частное
решение данного уравнения, правя часть
которого
частное
решение данного уравнения, правя часть
которого![]()
Учитывая
стандартную формулу правой части,
находим
![]()
Число
![]() не совпадает с
не совпадает с![]()
![]() подбираем
с учётом этого
подбираем
с учётом этого
![]()
Найдём
![]()
![]()
![]()
Общее решение данного уравнения
![]()
Найдём
частное решение, взяв
![]() для отыскания
для отыскания![]()
![]()
В
равенства (1) и (2) подставим начальные
условия:
 , тогда
, тогда
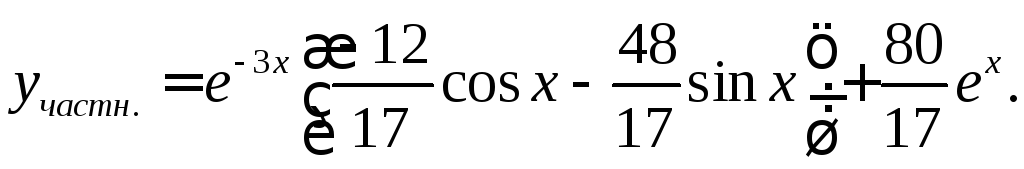
Тема
«обыкновенные дифференциальные уравнения
рассмотрена в пособии Высшая математика
в упражнениях и задачах ч.![]() ,
гл.
,
гл.![]() ,
П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова.
,
П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова.
Задание 371-380.
Вычислить
двойной интеграл
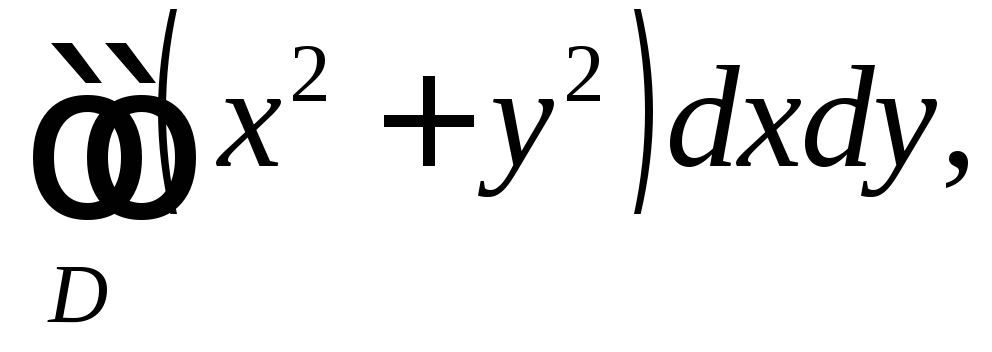 если областьD
ограничена окружностями
если областьD
ограничена окружностями
![]()
Необходимо перейти к полярным координатам, используя формулы перехода
![]()

Интеграл,
звисящий от
![]() ,
берём по частям
,
берём по частям

В
результате

Задание 391-400.
Вычислить
криволинейный интеграл по дуге
![]() линии, заданной параметрически
линии, заданной параметрически

Тогда

![]()
![]()
![]()
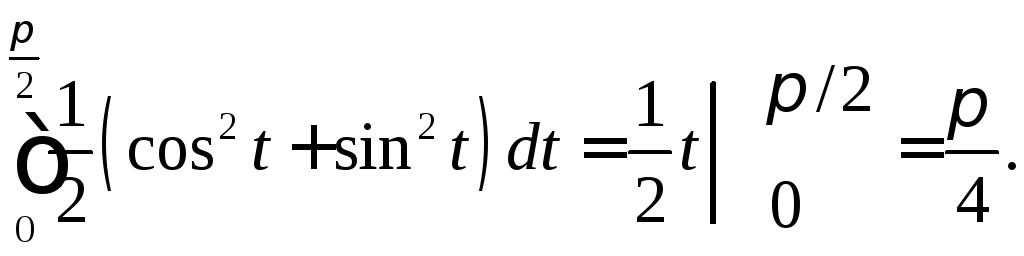
Задание 421-430
Исследовать сходимость числового ряда

Для исследования данного ряда применяем признак Даламбера:
 ,
ряд расходящийся,
,
ряд расходящийся,
![]() сходящийся,
сходящийся,![]() нет ответа по данному признаку.
нет ответа по данному признаку.
 по
данному условию, составим
по
данному условию, составим

Значит данный ряд сходящийся.
Задание 431-440
Найти область сходимости степенного ряда

Прежде всего определяется радиус сходимости степенного ряда
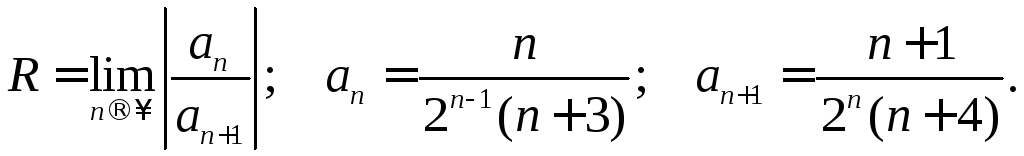
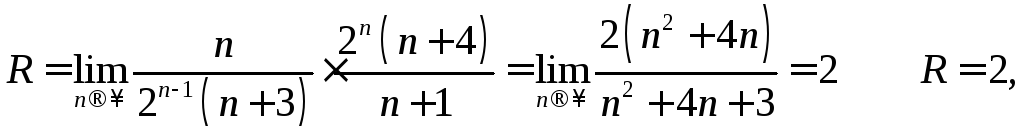
Значит
интервал сходимости
![]()
На границах интервала рассматриваются числовые ряды.
При

Так
как предел
![]() то ряд считается расходящимся.
то ряд считается расходящимся.
При![]()
 –
знакочередующийся ряд.
–
знакочередующийся ряд.
1. Рассмотрим члены ряда по абсолютной величине
![]()
Члены
ряда возрастают, значит по теореме
Лейбница при
![]() ряд расходящийся.
ряд расходящийся.
Задание 441 – 450
Вычислить
определённый интеграл
 с точностью 0,001,
с точностью 0,001,
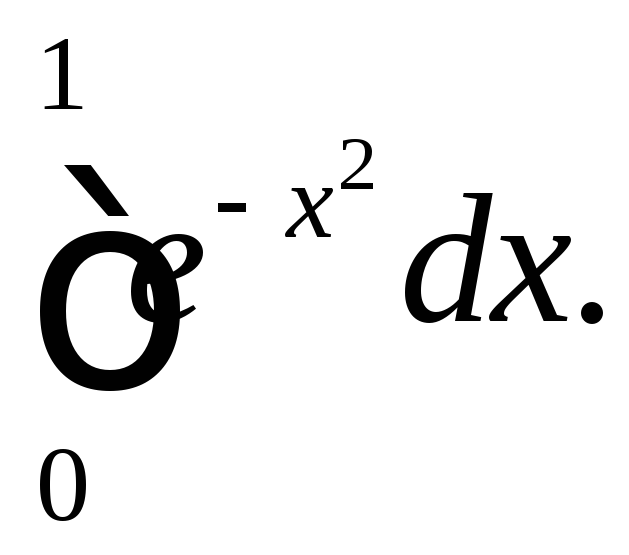 Разложим подынтегральную функцию в
ряд, а затем проинтегрируем её почленно.
Разложим подынтегральную функцию в
ряд, а затем проинтегрируем её почленно.

![]()
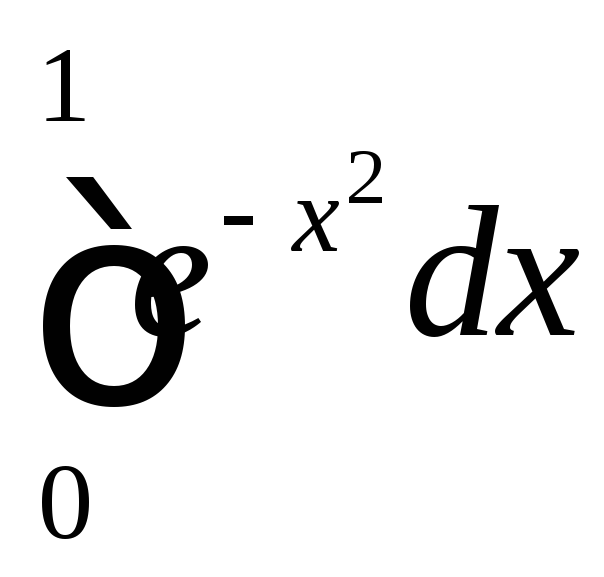 .
.
Используя разложение в ряд Маклорена функции
 ,
запишем разложение
,
запишем разложение

Проинтегрировав, получим:

Значение интеграла (по теореме Лейбница) соответствует сумме с точностью 0,001.

Шестое
слагаемое ,
![]() поэтому
взято пять слагаемых.
поэтому
взято пять слагаемых.
Типовые
задачи по теме «Ряды» рассматриваются
в учебном пособии П.Е.Данко, А.Г.Попов,
Т.Я.Кожевникова. Высшая математика в
упражнениях и задачах, ч.![]() ,
гл.
,
гл.![]() ,§§1-6.
,§§1-6.
451 – 460.
Найти
три первых отличных от нуля члена
разложения в степенной ряд решения
![]() дифференциального уравнения
дифференциального уравнения![]() удовлетворяющего данному условию
удовлетворяющего данному условию![]()
Используем
разложение искомой функции в ряд Тейлора
около точки
![]() .
.
![]()
В
нашем примере
![]() т.е. первый член ряда обращается в ноль.
т.е. первый член ряда обращается в ноль.
Из заданного дифференциального уравнения
![]()
Поэтому
второй член ряда имеет вид
![]() .
Чтобы найти третий член ряда
продифференцируем обе части нашего
уравнения
.
Чтобы найти третий член ряда
продифференцируем обе части нашего
уравнения

И
поэтому следующий член ряда равен
![]() .
Аналогично
.
Аналогично

Третий нулевой член ряда
![]()
Окончательно:
![]()
Интегрирование
дифференциальных уравнений с помощью
рядов рассматривается в учебном пособии
П.Е.Данко, А.Г.Попов, Т.М.Кожевникова.Высшая
математика в решениях и задачах, ч.![]() гл.
гл.![]() ,
§4.
,
§4.
