51 – 60.

Дана система линейных уравнений

Решить систему а) матричным методом, б) методом Крамера, в) методом Гаусса.

а) данной системе соответствует матричное уравнение , которое решается по формуле:. Матрицы имеют вид:

Находим обратную матрицу

Находим матрицу

б) - формула Крамера. Вычислим все определители

в) Метод Гаусса.

Составим расширенную матрицу и преобразуем её с помощью элементарных преобразований.

Из полученной матрицы, выделяя последнюю строку, видим, что исключены неизвестные и. Найдём..

Вторая строка соответствует уравнению:

или

Аналогично из первой строки напишем уравнение:

Итак:

91 – 100.

Дано комплексное число

Записать число в геометрической и тригонометрической формах и найти все корни уравнения

Рекомендуемая литература : Данко П.Е., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, ч. II, гл.III, §7, стр.97 – 101.

Найдём алгебраическую форму комплексного числа

Тригонометрическая форма комплексного числа определится по формуле.

Изобразив число на плоскости, найдём и.

_-1

_{Итак, число}

_{Найдём корни уравнения}

_{вычислим по формуле Муавра}

111 – 120.

_{Вычислить пределы:}

_а)

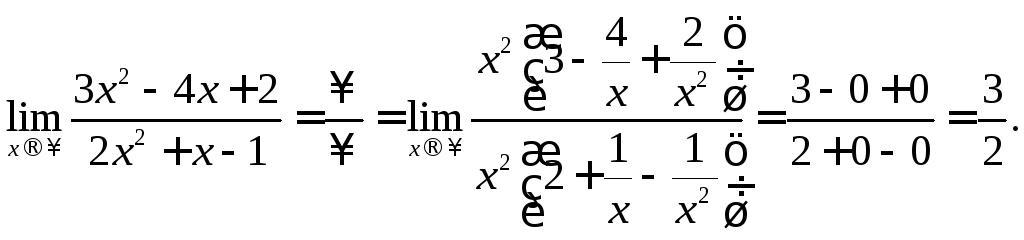
_{За скобку выносили наивысшую степень для числителя и знаменателя.}

_б)

_{Для исключения неопределённости требуется числитель и знаменатель разложить на множители.}

_в)

_{В данном случае для исключения неопределённости использованы эквивалентные бесконечно малые ,например}

_г)

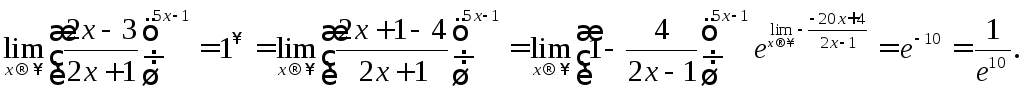
_д)

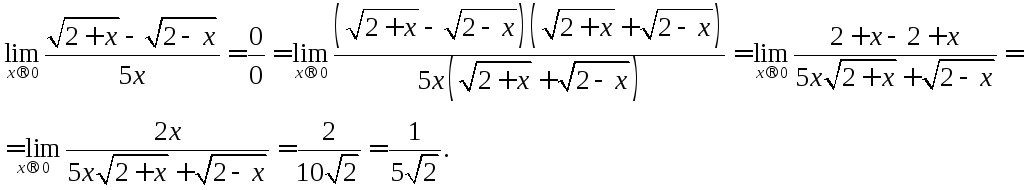
_{Числитель и знаменатель умножаем на выражение, сопряжённое числителю.}

_{Задания 111 – 120}

Задана функция Найти точки разрыва, если они существуют.

Сделать чертёж.

.

Кусочно-заданная функция представлена функциями, непрерывными на данных интервалах.

Проверим непрерывность в граничных точках.

найдём односторонние пределы

Левосторонний и правосторонний пределы равны и равны значению функции в точке . Значит функция в этой точке непрерывна.

аналогично

Пределы различны, значит в точке функция имеет разрыв с конечным скачком.

График функции выполните самостоятельно.

Обратите внимание на вспомогательноеучебное пособие

Данко П.Е., Попов Л.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах ч.I , гл.IV, §§4 – 6.

Задания 141– 150

Найти производные следующих функций:

а) б);

в) г);

д) .

б)

в)

г)

Прологарифмируем обе части равенства

Продифференцируем обе части равенства

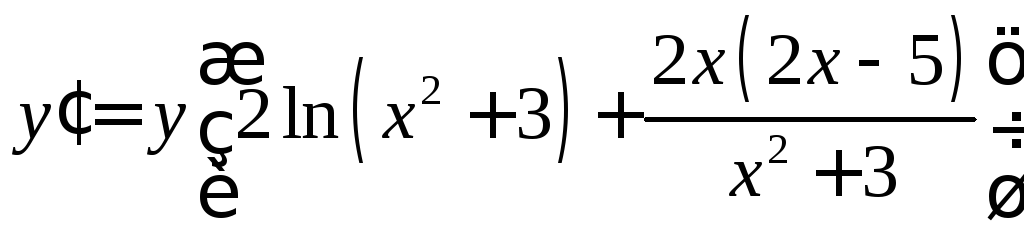
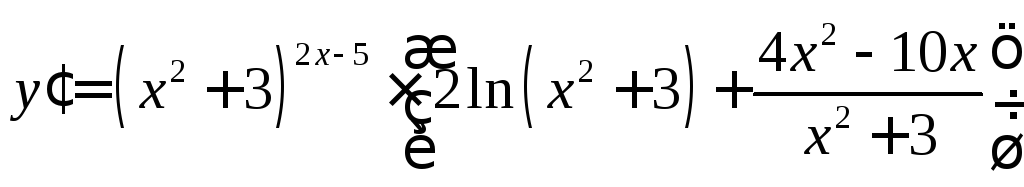
д)

Функция задана неявно. Учитываем, чтоаргумент,функция.

151 – 160.

_{Найти 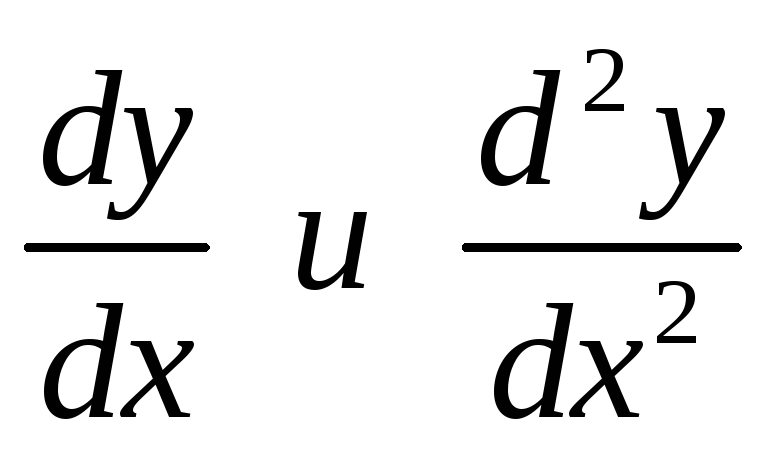функций:}

Решение:

а)

б)

191 – 200 .

Исследовать методами дифференциального исчисления функцию и построить её график.

Рассмотрим свойства функции:

1. Область определения:

2. Чётностьь, нечётность функции:

Функция общего вида.

3. Асимптоты.

а) Так как , то прямаяявляется вертикальной асимптотой:

б) _– наклонная асимптота.

Найдём

Найдём

_{– уравнение наклонной асимптоты.}

_{4. Найдём точки экстремума и интервалы монотонности функции:}

Так как то действительных корней нет, значит, нет точек экстремума.

Производная на всей области определения, значит функция

убывает.

5. Точки пересечения с координатными осями

а) с осью при,

б) с осью при.

Используя исследование функции, строим график (схематично).

Задания 141-150, 151-160, 191-200 легко выполнить, используя учебное пособие П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах ч.I гл. VII §§ 1-2 стр. 151-183.