7. Двойные и криволинейные интегралы

351-360. Вычислить двойные интегралы по области D.

351., гдеD – область, ограниченная линиям

352. , гдеD – область, ограниченная линиями

353. , гдеD – область, ограниченная линиями

354. , гдеD – область, ограниченная линиями

355. гдеD – область, ограниченная линиями

356. , гдеD – область, ограниченная линиями

357. гдеD – область, ограниченная линиями

358. гдеD – область, ограниченная линиями

359. , гдеD – область, ограниченная линиями

360. гдеD – область, ограниченная линиями

.

361 – 370. Перейдя к полярным координатам, вычислить площадь фигуры, ограниченной областью D.

361. Область D ограниченна линиями: (І четв.)

362. Область D ограниченна линиями: .(І четв.)

363. Область D ограниченна линиями: . (І четв.)

364. Область D ограниченна линиями:

365. Область D ограниченна лемнискатой: (І четв.)

366. Область D ограниченна линиями:

367. Область D ограниченна линиями:

368. Область D ограниченна линиями:

369. Область D ограниченна линиями:

370. Область D ограниченна лемнискатой:

371 – 380. Вычислить криволинейные интегралы

371. гдеL – контур треугольника, образованного осями координат и прямой в положительном направлении, т.е. против движения часовой стрелки.

372. гдеL – дуга параболы от точки О (0;0) до точки

А(2;4).

373.гдеL – контур прямоугольника, образованного прямыми

в положительном направлении (против часовой стрелки).

374. вдоль кривой.

375. вдоль кривойот точки О (0;0) до точки А(1;1).

376. вдольотточки О (0;0) до точки А(1;1).

377. , гдеL – четверть окружности 0, против часовой стрелки.

378., гдеL – первая арка циклоиды 0.

379. вдоль линииот точки О (0;0) до точки А(1;1).

380. вдоль отрезка ОА, О (0;0),.

8. Ряды

421-430. Исследовать сходимость числового ряда.

421. . 422..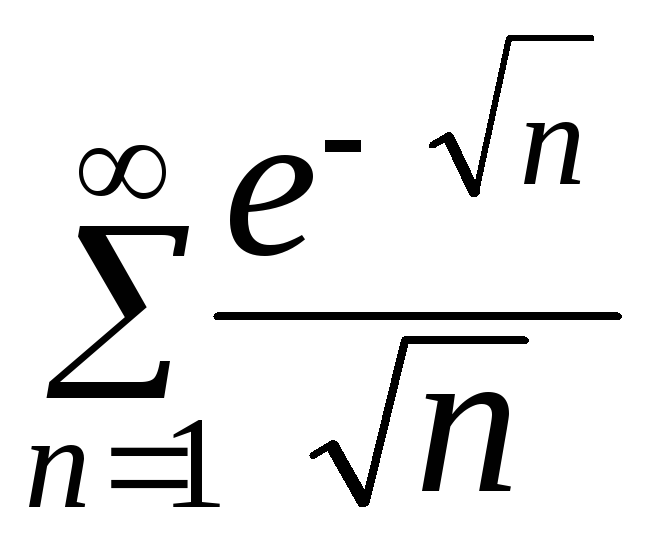

423. . 424..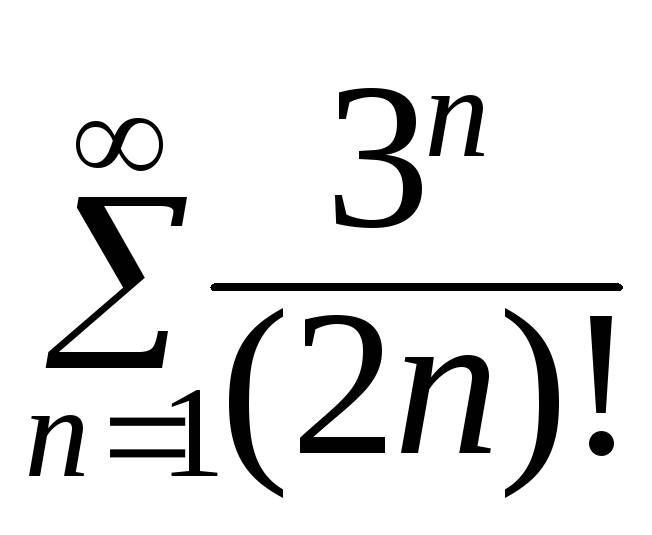

425. . 426..

427. . 428..

429. . 430..

431-440. Найти интервал сходимости степенного ряда.

431. . 432..

433. . 434..

435. . 436..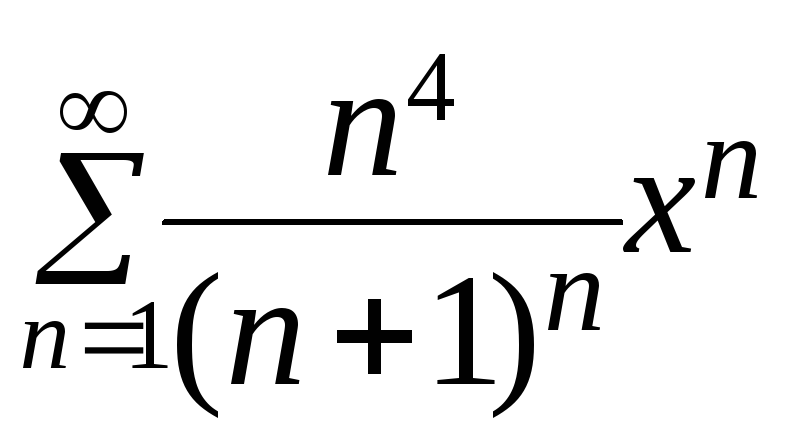

437. . 438..

439. . 440..

441-450. Вычислить определенный интеграл 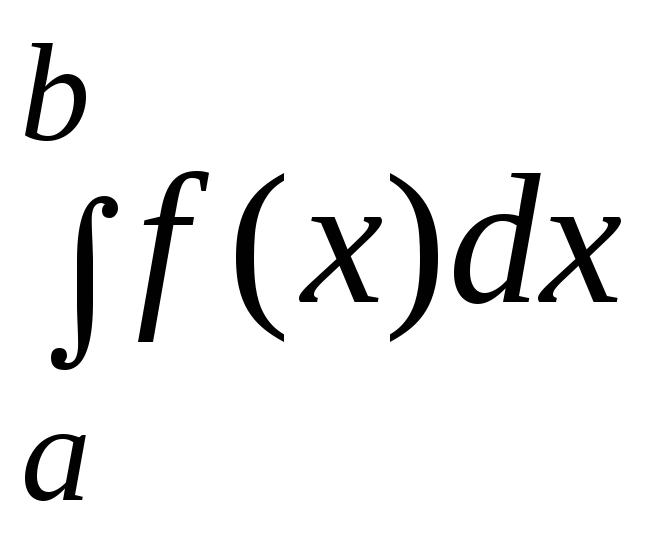с точностью до 0,001, разложив подынтегральную функцию в ряд, и, затем, проинтегрировав ее почленно.

441. . 442..

443. . 444..

445. . 446..

447. . 448..

449. . 450..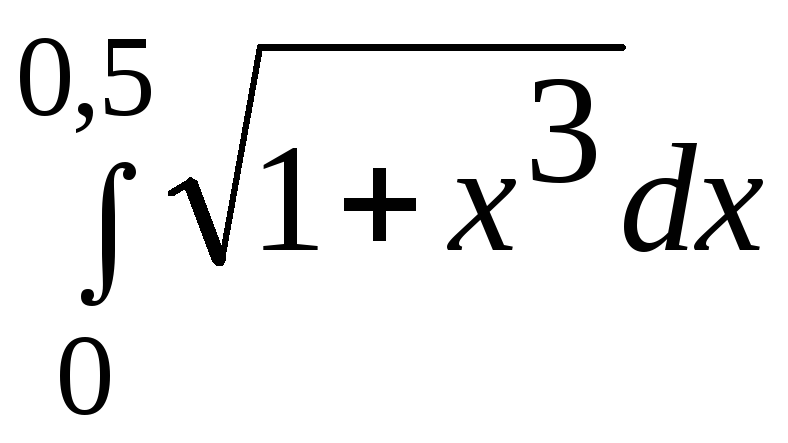

451 – 460. Найти три первых отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения, удовлетворяющего начальному условию.

451.

452.

453.

454.

455.

456.

457.

458.

459.

460.

461 – 470. Разложить данную функцию в ряд Фурье в интервале.

461. в интервале

462. в интервале

463. в интервале

464. в интервале

465.в интервале

466. в интервале

467. в интервале

468. в интервале

469. в интервале

470. в интервале

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ ЗАДАНИЙ

11 – 20.

Для решения задач 11 – 20 рекомендуется учебное пособие

Данко П.Е., Кожевникова Т.Я. Высшая математика в упражнениях и задачах.

Ч.1. М.: Оникс 21 век. 2005. Гл. I –IV, стр.39 – 91.

Рассмотрим решение аналогичной задачи, взяв координаты вершины пирамиды SABC: А(-3;0;0); В(0;2;0); С(0;0;6); S(-3;4;5).

1) Длину ребра АВ находим по формуле:

2) Угол между рёбрами найдём по формуле косинуса угла между векторами, координаты которых определяются так:

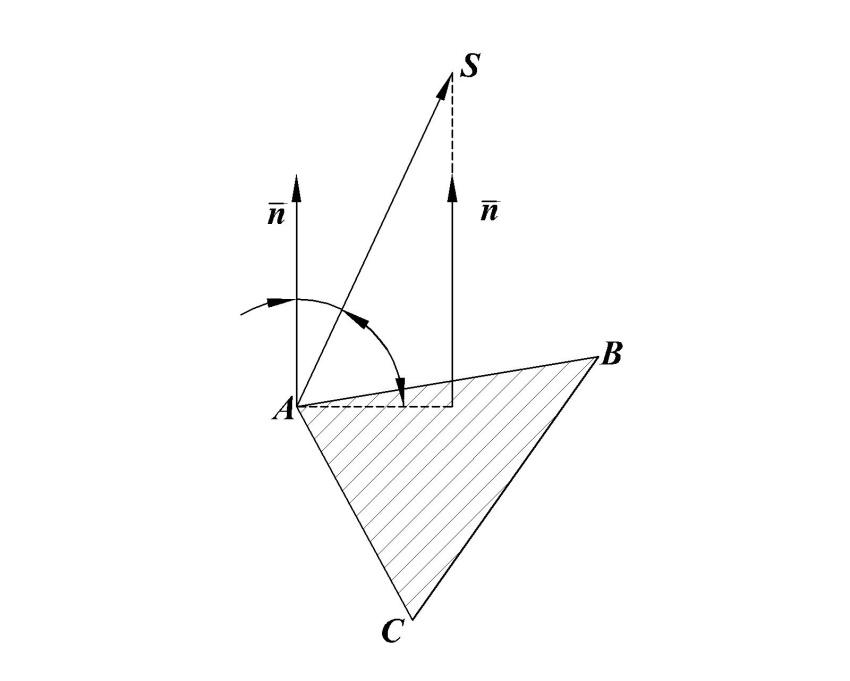
_α

Для решения задания 3) целесообразно решить задачу 7). Уравнение плоскости составим по уравнению

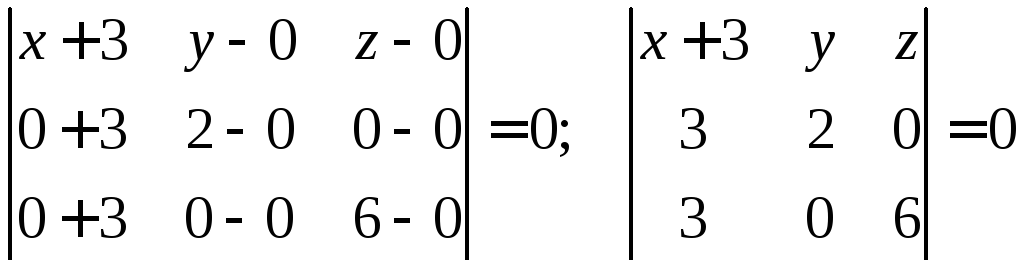
Нормальный вектор этой плоскости

4) Площадь определяем с помощью векторного произведения:

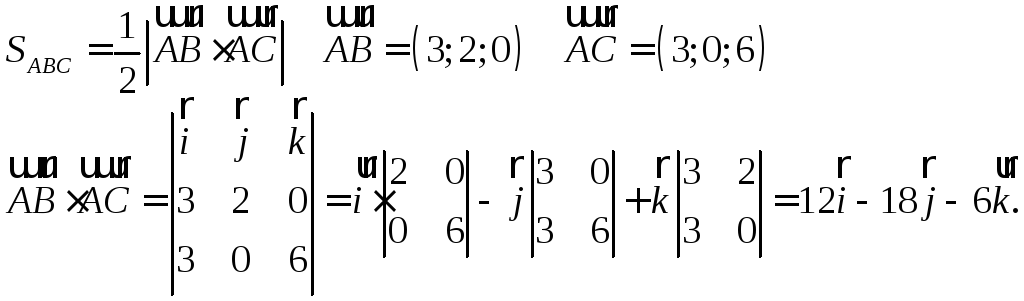
5) Объём пирамиды находится через вычисление смешанного произведения векторовИзучите понятие смешанного произведения, формулу объёма пирамиды и формулу для вычисления смешанного произведения трёх векторов. Решите самостоятельно.

6) Уравнение прямой

Канонические уравнения прямой, вектор направляющий вектор прямой

8) Для определения проекции вершины на плоскостьвыполняютсяследующие действия:

а) составляется уравнение высоты пирамиды .

б) находится точка пересечения высоты и основания решением системы, содержащей уравнение высоты и уравнение плоскости.

Решение: вектор удобнее взять

Он будет направляющим для По уравнению

вершина , т.е.

.

Система решается подстановкой

Подставив во второе уравнение, найдём значение , а следовательно значения

Точка - проекция точкина плоскость

9) Длину высоты пирамиды можно найти по формулеили по формуле расстояния от точки до плоскости – наиболее удобно.

Изучите формулы самостоятельно, решив задание 9).