Рабочие программы / Статистическая физика / (9 сем) Сверхпроводимость / Сверхпроводимость (методичка)

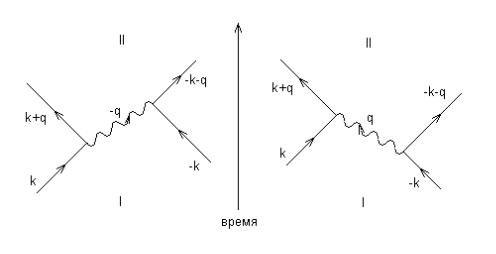
Рис. 14: Диаграммы обмена фононом между двумя электронами

Вторая диаграмма соответствует процессу, когда электрон 2, обладающий волновым вектором ¡k, испускает фонон с волновым

вектором q и энергией h!¹ q. В промежуточном состоянии имеется электрон 1 с волновым вектором k, электрон 2 с волновым век-

тором ¡ (k + q) и фонон с волновым вектором q. Энергия этого промежуточного состояния

"2 = »k + »k0 + h!¹ q;

ò.å.

"2 = "1:

Эти диаграммы соответствуют второму порядку теории возмущений по электрон-фононному взаимодействию. Первый порядок теории возмущений нас не интересует, поскольку он соответствует не обмену фононом между двумя электронами, а рассеянию одного электрона на фононе.

Во втором порядке теории возмущений матричный элемент, связывающий состояния I è II, имеет вид

(55) где суммирование производится по всем допустимым промежуточ- ным состояниям, Ueph - гамильтониан электрон-фононного взаи-

модействия. Обозначим посредством Wq матричный элемент, со- ответствующий испусканию или поглощению фонона с волновым

21

вектором q. Тогда

Äëÿ ! < !q член, соответствующий обмену фононом, отрицате-

лен. Таким образом, результирующее взаимодействие может представлять собой притяжение, если член Uc (q) не слишком велик.

Характерная частота фононов !q порядка дебаевской частоты !D

(напомним, что (¹h!D = k0£), ãäå £ - температура Дебая). Поэто-

му интервал значений энергии, в котором существует притяжение, имеет величину порядка k0£. Если температура Дебая £ порядка

300 K òî k0£ » 0:03 eV . Поскольку область притяжения является

узкой, то и энергия связи куперовской пары (ширина запрещенной щели) оказывается малой, а критическая температура перехода электронов в конденсированное состояние низкой.

По поводу изотопического эффекта. Частоты фононов !

p q и дебаевская частота !D обратно пропорциональны Mi, ãäå Mi - ìàñ-

са ионов решетки. Поэтому два изотопа одного и того же вещества имеют разную ширину области притяжения и их температуры перехода несколько отличаются. Этим объясняется изотопический эффект.

5Возбужденные состояния сверхпроводника

Мы показали, что сверхпроводящее состояние представляет собой конденсированное состояние электронов проводимости, которые связаны в куперовские пары (k "; ¡k #). Энергия связи пары, т.е.

ширина щели пропорциональна дебаевской температуре:

à 2 !

Eg = 2k0£ exp ¡U½ : (59)

22

Ïðè T = 0 все электроны связаны в пары. Пары обладают нуле-

вым спином и, следовательно, подчиняются статистике Бозе. При T = 0 они все находятся в состоянии с нулевой энергией. Такое

состояние Бозе-газа называется Бозе-конденсатом.

При низких, но конечных температурах T < Tk, помимо ку-

перовских пар, существуют нормальные возбуждения. Их спектр располагается выше щели и является непрерывным. В квантовой теории сверхпроводимости доказывается, что закон дисперсии нормальных возбуждений имеет вид:

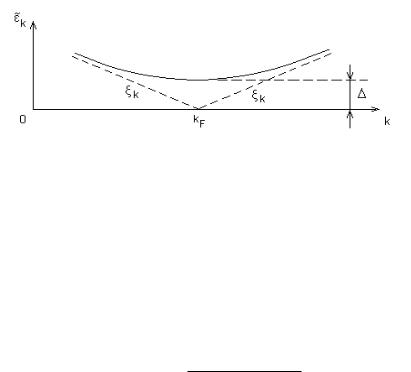
Он изображен на рис. 15.

Рис. 15: Спектр нормальных возбуждений в сверхпроводнике

Наличие щели в спектре нормальных возбуждений и означает, что сверхпроводящее состояние является конденсированным: для создания возбужденного состояния требуется конечная энергия ¢.

Нормальные возбуждения обладают спином 1/2 и подчиняются статистике Ферми. Число равновесных нормальных возбуждений при температуре T < Tk определяется функцией Ферми

Ïðè k0T ¿ ¢ число нормальных возбуждений экспоненциально

Это объясняет, почему при T ¿ Tk электроны дают экспоненци-

ально малый вклад в теплоемкость и в поглощение микроволнового излучения.

23

6Незатухающие токи в сверхпроводниках

Существование незатухающих токов и их исключительную устой- чивость можно объяснить на основе представления об элементарных возбуждениях в сверхпроводниках. При этом важно, что энергетическая щель, отделяющая спектр нормальных возбуждений от конденсата, не связана с кристаллической решеткой; ее положение в k-пространстве не привязано к границам зоны Бриллюэна,

как в полупроводниках; она просто расположена на уровне Ферми. Поэтому наличие щели не препятствует существованию токового состояния, которое соответствует движению токового конденсата как целого со скоростью v. Â k-пространстве конденсат сдвигает-

ся на величину ±k = mv=h¹. Энергетическая щель не препятствует

этому сдвигу; она перемещается вместе с поверхностью Ферми в новое положение. Такое токовое состояние весьма устойчиво. Чтобы затормозить конденсат, необходимо передать его импульс решетке или нормальным возбуждениям. Однако наличие щели затрудняет такой процесс и при определенных условиях делает его невозможным. Рассмотрим сверхпроводник, в котором электронный конденсат движется со скоростью v. Чтобы импульс конден-

сата мог измениться, в системе должно появиться новое элементарное возбуждение. Пусть импульс возникшего возбуждения равен h¹k, а его энергия "~k. Тогда законы сохранения энергии и

импульса имеют вид

ãäå M0 - масса всего конденсата, а v0 - его скорость после рождения возбуждения. Выражая v0 из (64) и подставляя в (63), получаем

h¹2k2

¡h¹k ¢ v + 2m + "~k = 0:

Масса конденсата M0 очень велика. Поэтому вторым слагаемым можно пренебречь и мы получаем условие

24

Возбуждение может возникнуть, если это неравенство выполняется по крайней мере в точке спектра, где отношение "ek=hk¹ ìèíè-

мально. Таким образом, условие, необходимое для рождения возбуждений, имеет вид:

Поэтому при скоростях движения конденсата v < vcr рождения

возбуждений не происходит и конденсат движется без трения, т.е. ток является незатухающим. Наоборот, при скоростях v > vcr äâè-

жение конденсата будет сопровождаться рождением возбуждений и ток будет затухать.

25