Рабочие программы / Статистическая физика / (9 сем) Сверхпроводимость / Сверхпроводимость (методичка)

СВЕРХПРОВОДИМОСТЬ

Удельное электрическое сопротивление многих металлов и сплавов резко падает до нуля, если образец охладить до достаточно низкой температуры. Это явление было впервые наблюдено Камерлингом Оннесом в 1911 г. на ртути. При понижении температуры от 4.23 К до 4.18 К сопротивление ртути упало более, чем в 10000 раз (рис. 1).

Рис. 1: Температурная зависимость сопротивления ртути в окрестности перехода

Явление получило название сверхпроводимости. Обычно говорят, что при критической температуре Tk образец испытывает фазовый

переход из нормального состояния в сверхпроводящее.

1Основные свойства сверхпроводящего состояния

1.1 Электрические свойства. Сопротивление постоянному току в сверхпроводящем состоянии равно нулю или настолько близко к нулю, что незатухающие сверхпроводящие токи в сверхпроводящем кольце наблюдались в течение полутора лет без скольконибудь заметного уменьшения.

1

1.2 Магнитные свойства. Эти свойства сверхпроводников не менее необычны, чем электрические. Экспериментально установлено, что массивный сверхпроводник в слабом магнитном поле ведет себя как идеальный диамагнетик, внутри которого магнитная индукция B = 0. Если образец поместить в магнитное поле, а за-

тем охладить до температуры ниже критической, то проходящий через образец магнитный поток полностью вытесняется из него. Это явление называется эффектом Мейсснера. Эффект Мейсснера в сверхпроводящей сфере, охлаждаемой в постоянном магнитном поле, изображен на рис. 2.

Рис. 2: Эффект Мейсснера в сферическом сверхпроводнике

При температурах, ниже критической, магнитные силовые линии выталкиваются из шара. Такие необычные магнитные свойства являются важнейшей характеристикой сверхпроводящего состояния.

1.3 Сверхпроводящие материалы. Сверхпроводимость на-

блюдается во многих металлических элементах таблицы Менделеева, в сплавах, интерметаллических соединениях и некоторых полупроводниках. Интервал температур перехода известных до 1985 г. сверхпроводников простирался от 0:01 K äî 23 K. Â 1985

г. было обнаружено, что ряд керамик из окислов меди, щелочноземельных металлов и некоторых редкоземельных элементов являются сверхпроводниками, имеющими намного более высокие критические температуры. Эти керамики получили название высокотемпературных сверхпроводников (ВТСП). В настоящее время известны ВТСП материалы с Tk около 100 K.

1.4 Разрушение cверхпроводимости магнитнам полем.

Достаточно сильное магнитное поле разрушает сверхпроводимость. Пороговая или критическая величина магнитного поля обозна-

2

чается посредством Hk (T ); она является функцией T . Ïðè êðè-

тической температуре критическое магнитное поле равно нулю: Hk (Tk) = 0. Изменение критического поля с температурой имеет

Рис. 3: Зависимость критического поля сверхпроводника от температуры

вид, изображенный на рис. 3. Это фазовая диаграмма сверхпроводника. Кривая Hk (T ) отделяет область сверхпроводящего со-

стояния от области нормального состояния. Значение критического поля сверхпроводника при абсолютном нуле Hk (0) тем больше,

чем выше его критическая температура Tk.

1.5 Классификация сверхпроводников. Рассмотрим подроб-

нее эффект Мейсснера, который заключается в том, что если сверхпроводник в магнитном поле охладить ниже температуры перехода, то магнитные силовые линии выталкиваются из образца, как будто внутри него магнитная индукция B = 0. В случае длинно-

го цилиндрического образца, ось которого параллельна внешнему магнитному полю H, это приводит к следующему результату для

магнитной восприимчивости сверхпроводника:

Таким образом, сверхпроводники являются идеальными диамагнетиками.

Для многих сверхпроводников кривая намагниченности имеет следующий вид:

3

Рис. 4: Кривая намагниченности сверхпроводника 1-го рода

Такие сверхпроводники называются мягкими или сверхпроводниками первого рода. При H > Hk намагниченность в таком сверх-

проводнике становится ничтожно малой и образец ведет себя как нормальный проводник. При H < Hk намагниченность M = ¡H=4¼;

отрицательный знак соответствует диамагнетизму. Величина 4¼M

это магнитное поле, создаваемое сверхпроводящими токами, индуцированными внешним магнитным полем. Критическое магнитное поле Hk в сверхпроводниках первого рода является довольно

низким, порядка 100 эрстед, и эти сверхпроводники не применяются в сверхпроводящих магнитах.

Для других сверхпроводников кривая намагниченности имеет форму, приведенную на рис. 5. Такие сверхпроводники называют-

Рис. 5: Кривая намагниченности сверхпроводника 2-го рода

ся жесткими или сверхпроводниками второго рода. К ним относятся главным образом сплавы и переходные металлы, имеющие высокое удельное электрическое сопротивление в нормальном состоянии, т.е. материалы с малой длиной свободного пробега электронов проводимости.

4

Сверхпроводники второго рода ведут себя как и сверхпроводники первого рода при H < Hk1. В интервале между Hk1 è Hk2

абсолютная величина M в них падает, хотя их электрические свой-

ства остаются сверхпроводящими. При значениях поля в этом интервале в сверхпроводнике образуются области, в которых магнитный поток имеет конечную величину, B =6 0 и эффект Мейсснера

является неполным. Такое состояние называется смешанным. В сверхпроводниках второго рода критическое поле Hk2 может до-

стигать величины в несколько сот килоэрстед. Эти сверхпроводники используются для создания сверхпроводящих магнитов.

1.6 Теплоемкость. В сверхпроводящем состоянии энтропия оказывается ниже, чем в нормальном состоянии при той же температуре (рис. 6).

Рис. 6: Температурная зависимость энтропии сверхпроводника

Переход в нормальное состояние при обеспечивается прложением сильного магнитного поля, которое разрушает сверхпроводимость.

Уменьшение энтропии в сверхпроводящем состоянии по сравнению с нормальным означает, что сверхпроводящее состояние является более упорядоченным. Электроны, которые термически возбуждены в нормальном состоянии, оказываются упорядоченными в сверхпроводящем.

Экспериментальные данные свидетельствуют о том, что теплоемкость электронов в сверхпроводящем состоянии изменяется с температурой по экспоненциальному закону. Если из теплоемкости сверхпроводника исключить фононный вклад и отложить логарифм электронной теплоемкости в сверхпроводящем состоянии как функцию Tk=T , то точки ложатся на прямую. Эксперимен-

тальные данные для галлия, хорошо описываемые формулой

Ce(T ) = C0 exp µ¡1:4TTk ¶ ;

5

приведены на рис. 7.

Рис. 7: Температурная зависимость электронной теплоемкости галлия при T < Tk

Такая зависимость свидетельствует о наличии запрещенной щели в энергетическом спектре электронов в сверхпроводящем состоянии. Зонная структура электронов схематически изображена на рис. 8. В сверхпроводящем состоянии в области уровня Ферми воз-

Рис. 8: Схема энергетических зон в нормальном и сверхпроводящем состояниях

никает запрещенная щель. Электроны в возбужденных состояниях над щелью ведут себя как обычные электроны проводимости. При абсолютном нуле электронов над щелью нет. Ширина щели мала, обычно Eg » 10¡4"F .

Природа энергетической щели с сверхпроводниках отличается от природы энергетической щели в диэлектриках. Обнаружено, что показатель экспоненты в температурной зависимости электронной теплоемкости представляет собой отношение половины

6

ширины щели к тепловой энергии k0T , ãäå k0 - постоянная Больц- мана. Так, в галлии Eg = 2:8 k0Tk. Такое значение отношения Eg=k0Tk является типичным. Полуширина щели Eg=2 обознача- ется символом ¢ и называется параметром энергетической щели.

Величина щели зависит от температуры. Она максимальна при абсолютном нуле и обращается в нуль при T = Tk. Зависимость

отношения Eg (T ) =Eg (0) îò T изображена на рис. 9.

Рис. 9: Изменение ширины щели с температурой

1.7 Высокочастотные свойства. Существование энергети-

ческой щели в сверхпроводниках означает, что фотоны с энергиями, меньшими ширины щели не могут поглощаться. Это подтверждается экспериментально. Поглощение фотонов с энергиями, меньшими ширины щели, при T = 0 обращается в нуль. Экспе-

риментальные результаты для микроволнового поглощения в алюминии приведены на рис. 10. Поглощение в сверхпроводящем со-

Рис. 10: Частотная зависимость поверхностного сопротивления алюминия

7

стоянии имеет резкий порог при энергии фотона, равной ширине щели. Фотоны меньшей энергии не поглощаются. Фотоны с энергиями, большими ширины щели, поглощаются, поскольку они вызывают переходы электронов в свободные состояния над щелью.

1.7 Изотопический эффект. Экспериментально установлено, что критическая температура сверхпроводника зависит от массы изотопа. Критическая температура ртути изменяется от 4:185 K

äî 4:146 K при изменении массы атомов от 199:5 äî 203:4 àòîì-

ãäå Mi - масса изотопа. Для ртути ® = 0:504.

Из того факта, что Tk зависит от массы изотопа Mi, следу-

ет, что колебания решетки и, следовательно, электрон-фононное взаимодействие играют важную роль в образовании сверхпроводящего состояния. В противном случае критическая температура Tk не зависела бы от числа нейтронов в ядре.

2Термодинамика сверхпроводящего перехода

Экспериментально доказано, что переход между нормальным и сверхпроводящим состояниями термодинамически обратим так же, как переход между жидкой и парообразной фазами вещества. Поэтому мы можем применить термодинамику к этому переходу. Будем рассматривать только сверхпроводники первого рода, в которых эффект Мейсснера является полным и B = 0. Покажем, что

Hk характеризует разность химических потен-

циалов нормальной и сверхпроводящей фаз. Условием равновесия фаз при постоянных T è P является, как известно, равенство хи-

мических потенциалов. Поэтому нам необходимо получить выражение для химического потенциала сверхпроводника в магнитном поле H, принимая во внимание, что в нем имеет место эффект

Мейсснера.

Основное термодинамическое тождество для бесконечно малого процесса в системе имеет вид

8

ãäå E - внутренняя энергия, S - энтропия, P - давление, а V -

объем системы. Если система находится во внешнем магнитном поле H, то к правой части термодинамического тождества добав-

ляется элементарная работа, производимая внешними токами по намагничиванию системы. Эта работа

¡±L = H ¢ d (MV ) ;

ãäå M - намагниченность (магнитный момент единицы объема),

MV - полный магнитный момент системы. Основное термодинамическое тождество принимает теперь вид

Условием равновесия системы при постоянных T è P является минимум термодинамического потенциала

Аналогично, условием равновесия системы при постоянных T , P è H является минимум термодинамического потенциала

Дифференциал этого термодинамического потенциала

d© (T; P; H) = ¡SdT + V dP ¡ V M ¢ d (H) :

Химический потенциал это термодинамический потенциал, отнесенный к одному молю вещества, т.е. дифференциал химического потенциала

9

Таким образом, химический потенциал сверхпроводника в магнитбольше чем в отсутствие поля на величину e 2

íîì ïîëå H VsH =8¼:

Химический потенциал нормального проводника можно счи- тать не зависящим от магнитного поля H, т.е. считать ¹n = ¹n (T; P ).

Мы знаем, что если химический потенциал первой фазы больше химического потенциала второй фазы, то первая фаза оказывается неустойчивой. Поэтому в достаточно сильных магнитных полях H > Hk сверхпроводящее состояние становится термодина-

мически невыгодным: ¹s (T; P; H) > ¹n (T; P ) и сверхпроводимость

Это уравнение кривой фазового равновесия. Оно определяет зависимость критического поля от температуры: Hk = Hk (T ) (ðàçó-

меется при этом T < Tk(H = 0)).

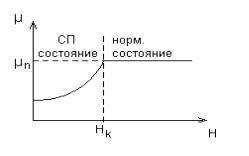
В более слабых магнитных полях H < Hk (T ) химический по-

тенциал сверхпроводящей фазы меньше химического потенциала нормальной фазы, так что в этой области устойчивым является сверхпроводящее состояние. Таким образом, зависимость химиче- ского потенциала сверхпроводника от H имеет вид:

Рис. 11: Зависимость химического потенциала сверхпроводника от магнитного поля

10