
- •Содержание
- •Предисловие
- •2.2. Напряжения
- •2.3. Связь напряжений и деформаций
- •2.4. Энергия деформации
- •2.5 Уравнения движения
- •Выведем теперь уравнения, определяющие передачу движений частиц упругой среды. Согласно законам механики, движение точки (элемента среды с массой dm) определяется уравнением
- •2.6.Сейсмические волны
- •2.7. Плоские волны
- •2.9. Сферические волны
- •Будем решать это уравнение в сферических координатах. Оператор Лапласа в сферических координатах имеет вид:
- •Для простоты предположим, что источник излучает одниково во всех направлениях, так что волновое поле является сферически симметричным, т.е. зависит только от координаты R. Тогда уравнение (2.34) принимает вид
- •2.10 . Энергия волны
- •2.11. Отражение и преломление волн на границах
- •Глава 3. Основы сейсмометрии
- •3.1. Движение маятника
- •Глава 9. Поглощающие свойства земных недp
- •9.1. Реологические модели
- •Чтобы понять, как влияет комплексность модулей на характер распространения волны, рассмотрим плоскую гаpмоническую волну, распространяющуюся в направлении оси х:
- •Запишем (9.9) в форме
- •Опpеделение добротности из сейсмических наблюдений.
Глава 3. Основы сейсмометрии
В 1875 году Филиппо Секки в Италии сконструировал сейсмограф, который включал часы в момент первого толчка и записывал первое вступление. Старейшая сейсмическая запись с помощью этого прибора датируется 1887 годом. После этого начинается быстрый прогресс в области создания инструментов для регистрации колебаний почвы. Группа английских ученых, работавших в Японии, основными среди которых были Милн, Юинг и Грэй, создали первую достаточно удобный в обращении прибор для записи колебаний от землетрясений (главным образом, близких). Вскоре после этого начинается создание и усовершенствование таких приборов в Европе, и в 1900 году уже функционировала мировая сеть из 40 станций, оборудованных приборами Милна. Далее эта сеть расширялась, а приборы для записи движения почвы усовершенствовались. Инструментальные наблюдения являются фундаментом, на котором выросла сейсмология как наука. Поэтому сейсмометрия - раздел сейсмологии, разрабатывающий инструментальные методы наблюдений, наряду с теорией сейсмических волн, является базовым в сейсмологии. Приборы, при помощи которых производится запись колебаний почвы, называются
сейсмографами.
Задачей сейсмометрии является получение информации о смещении точек земной поверхности (“почвы”) под действием упругих волн в Земле. Смещения почвы можно было бы легко измерить, если бы была возможность установить датчик в инерциальной системе координат, связанной с недеформируемой вращающейся Землей. Однако, это невозможно, так как приборы располагаются на реальной (деформируемой) поверхности Земли и перемещаются одновременно со смещениями почвы. Это создает принципиальное отличие сейсмометрии от наблюдений в других областях физики. Поэтому для регистрации смещений почвы используются принцип инерции: маятник или груз, подвешенный на пружине, в силу инерции не будет мгновенно следовать движению подвеса, связанного с почвой. Поэтому движение маятника относительно подвеса будет в какой-то степени отражать движение почвы относительно инерциальной системы координат. Другой способ, хотя и не получивший широкого распространения в силу конструктивных сложностей, - это измерение деформаций, т.е. относительного перемещения двух разнесенных точек земной поверхности.
Структурно сейсмограф состоит из собственно маятника той или иной конструкции и системы регистрации колебаний маятника. До 1902 года, когда Б.Б.Голицын предложил способ преобразования механических колебаний в электрический ток, колебания маятника регистрировались непосредственно механическим или оптическим способом. Такой способ, называемый прямой регистрацией, до сих пор используется при записи сильных движений в сейсмически активных зонах, где движения почвы достаточно велики. Но для регистрации колебаний от слабых землетрясений и на больших расстояниях от очагов требуется усиливать колебания маятника, и это осуществляется различными преобразователями механических перемещений в электрический ток. При этом очевидно, что и колебания маятника относительно подвеса, и тем более, колебания индуцируемого электрического тока, не идентичны колебаниям почвы. Поэтому в задачу сейсмометрии входит не только
59
создание приборов, реагирующих на колебания грунта, но и определение связи между истинными движениями почвы и записями, получаемыми этими приборами.
3.1. Движение маятника
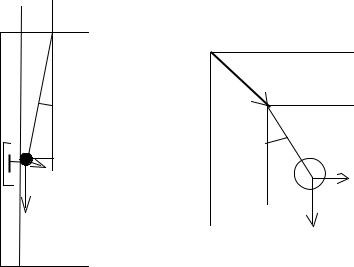
Принцип регистрации приборами маятникового типа легко понять из рассмотрения движения обычного математического маятника, точка подвеса которого связана с землей и перемещается по некоторому закону.
Пусть u(t) смещение почвы относительно инерциальной системы координат
(рис.3.1а), ξ(t) смещение маятника по отношению к почве (подвесу), М - масса маятника, l - его длина.
Следует учесть еще и силу демпфирования, действующую на маятник. Она пропорциональна скорости движения маятника относительно подвеса. (в простейшем случае это воздушное сопротивление и сила трения в подвесе).
u
l θ |
u |
|
x |
||
|
||
ξ |
θ |
|
.. |
||
|
||
|
Mux |
|
Mg |
z Mu |
|
|
.. |
|
|
z |
|
а |
б |
Рис.3.1 а –схема математического маятника, б –схема физического маятника
Смещение маятника относительно инерциальной системы координат будет
u(t)+ ξ(t). Таким образом, уравнение движения маятника можно записать в следующем виде:
|
d 2 |
|
|
|
|
dξ |
|
|
ξ |
|
|
ξ |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M dt2 (u +ξ) |
+ |
b dt |
+ |
Mg l |
= |
0 |
≈ sinθ |
||||||||||
l |
|
||||||||||||||||
сила инерции |
сила |
|
возвращающая |
|
|
|
|
||||||||||
|
|
|
демпфирования |
|
|
сила |
|
|
|
|
|
||||||
Обозначим: |
b |
|
= 2ε, |
|
ωs2 = |
g |
, тогда уравнение движения маятника примет вид: |
||||||||||
M |
|
l |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
|
|
|
|
(3.1) |
|
|
|
|||
ξ + 2εξ +ωs ξ = −u |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
60

В случае физического маятника (рис.3.1б) для вывода уравнения движения следует приравнять нулю сумму всех моментов сил, действующих на маятник. Обозначим:
I - момент инерции маятника,
θ - угол (малый) отклонения маятника от вертикальной оси ,
b - коэффициент пропорциональности в выражении для момента сил затухания, С - коэффициент пропорциональности в выражении для момента возвращающей
силы. Тогда
Iθ +bθ + Cθ = −M y
где My - момент инерциальных сил. Компоненты силы инерции равны соответственно Mux , Muy , Muz . Эта сила приложена к центру тяжести маятника.
Если маятник может колебаться только в плоскости xz, то очевидно, что y - компонента силы не создает момента. При малых углах отклонения достаточно рассматривать только х-компоненту силы. Если расстояние от центра тяжести маятника до оси вращения равно R0, то момент равен Mux R0. Таким образом, уравнение движения физического маятника будет иметь вид аналогичный (3.1):
|
|
|
|
|
|
|
|
θ + 2εθ |
+ωs2θ |
= − |
ux |
, |
(3.2) |
||
|
|||||||
|
I |
|
|
|
l |
|
|
где l = |
|
- приведенная длина, т.е. длина такого математического маятника, |
|||||
MR |
0 |
||||||
|
|
|
|
|
|
|
|
b
который имеет ту же частоту собственных колебаний, 2ε = I .
Изображенный на рис.3.1 маятник отклоняется от положения равновесия при горизонтальных движениях почвы. Вертикальные движения можно регистрировать, например, при помощи массы М, подвешенной на пружине. Пусть жесткость
пружины K , ее длина l, вертикальное смещение почвы u(t) , растяжение пружины
ξ(t) . Тогда уравнение движения массы относительно инерциальной системы координат будет иметь вид
M |
d 2 |
(u +ξ) + |
b |
dξ |
+ |
K |
ξ |
= 0 |
(3.3) |
|
|
|
dt2 |
dt |
l |
K |
|
||||||||
|
|
|
|
|
|
|
|
|||||
Это уравнение также приводится к каноническому виду (3.1) , в котором ωs2 = |
. |
|||||||||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
Ml |
||
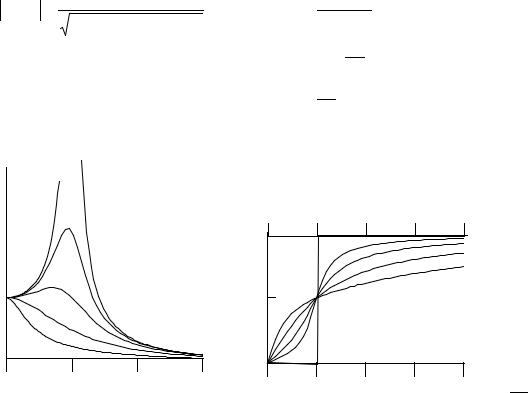
Частотная характеристика
Уравнение (3.1) или (3.2) описывает линейную систему. Ее частотную характеристику получим, если примем входной сигнал в виде гармонического колебания: u(t) = exp(iωt) . Тогда ξ (t) = X (ω)exp(iωt) , и подстановка этих
выражений в (3.1) даст
−ω2
X (ω) = ω2 − 2iεω −ωs2
Соответственно амплитудная и фазовая характеристики будут следующими:
61
|
X (ω) = |
|
ω2 |
|
|
2εω |
|
|
|
|
|
|
(ω2 |
−ωs2 )2 |
+ 4ε 2ω2 |
γ (ω) = arctg ω2 |
−ωs2 |
|
|
|
|||
При разных значениях постоянной затухания D = ε |
|
амплитудная и фазовая |
|||||||||
|
|
|
|
|
|
1 |
ω |
s |
|
|
|
|
|
|
|
|
|
ωs |
|
|
|
|
|
характеристики в зависимости от величины u = |
имеют вид, изображенный на рис. |
||||||||||
3.2. Цифры у кривых – значения D1 . |
ω |
|
|
|
|
|
|||||
|
|
|
|
|
|
||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0.25 |
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
0.25 0.5 |
1 |
|
||||
|
|
|
|
|
|
|
|||||
1 |
0.5 |
|
|
π/2 |
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
0 |
1 |
|
2 |
3 |
4 u = |
ωs |
|
амплитудная характеристика |
фазовая характеристика |
|
ω |
|||||||
|
|
|
|||||||||
|
Рис.3.2 |
Частотные характеристики маятника |
|
|
|
|
|||||
Из рассмотрения амплитудной характеристики видна важность затухания маятника: оно обязательно должно присутствовать, чтобы погасить собственные колебания, которые искажают частотный состав входного сигнала. Затухание может быть осуществлено разными способами, но наиболее распространенный и используемый в настоящее время во всех приборах – это электромагнитное затухание. Индукционная катушка, соединенная с массой маятника и замкнутая на внешнее сопротивление, находится в магнитном поле магнита, укрепленного на основании прибора. При движении маятника в катушке индуцируется электрический ток, магнитное поле которого, взаимодействуя с полем постоянного магнита, создает тормозящий момент. Величина затухания легко регулируется внешним резистором.
С увеличением периода амплитудная характеристика спадает как Т-2. Чтобы поднять увеличение на больших периодах, выгодно увеличить Тs, т.е. собственный период маятника. Увеличение собственного периода достигается специальной конструкцией подвесов.
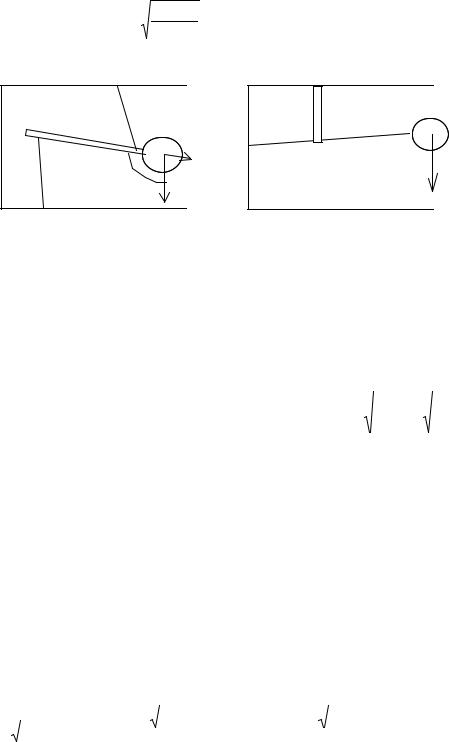
При регистрации горизонтальных колебаний используют цельнеровский подвес(рис.3.3а) : маятник колеблется не в вертикальной плоскости, а в плоскости, наклоненной под углом θ к вертикали. За счет этого на него действует не сила тяжести, а ее составляющая, равная Mg cosθ , и тогда собственный период
62
оказывается равным ωs = |
g cosθ |
. Период можно существенно увеличить, если θ |
|||
близко к π/2. |
|
l |
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
gcosθ |
R |
|
|
|
θ |
|
|
|
|
|
g |
|
б |
|
|
|
а |
|
|
|
|
Рис.3.3. |
Конструктивные способы |
увеличения |
собственного периода |
||
колебаний маятника |
|
|
|
|
|
При регистрации вертикальных колебаний используют схему на рисунке 3.3б. Собственные колебания определяются из уравнения равенства моментов:
Id 2θ2 + Kθr 2 = 0
dt
откуда период собственных колебаний равен ωs = |
Kr 2 |
= |
|
Kr 2 |
|
, где l - |
I |
|
MRl |
|
|||
|
|
|
|
|
приведенная длина. Уменьшение собственной частоты достигается уменьшением r по сравнению с R и l.
Собственные колебания сейсмографа
При подаче на вход колебательной системы импульса, имитирующего дельтафункцию, система будет совершать собственные колебания. Исследование такого типа колебаний важно, так как с его помощью можно выразить движение, обусловленное произвольным во времени импульсом u(t) .
Итак, задача сводится к решению уравнения:
θ + 2εθ +ωs2θ = −δ (t)
Его решение будет иметь вид: |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
t < 0 |
|
|
|
|
|
|
|
|
|
||
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|||||
θ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
[exp(−(ε + ε |
2 |
2 |
))t)− exp(−(ε − |
|
2 |
2 |
))t)] |
||||||
|
|
|
|
|
|
|
−ωs |
ε |
|
−ωs |
||||||
|
|
|
|
|
|
|
||||||||||
2 |
ε |
2 |
2 |
|
|
|||||||||||
|
|
−ωs |
|
|
|
|
|
|
|
|
|
|
|
|
||
Справедливость этого решения легко проверить, т.к. при следовательно, θ = −ε (t), а значит, θ = −δ (t).
Рассмотрим частные случаи:
t > 0
t = +0 θ = −t , а
63

|
ω |
|
> ε . Обозначая ω = |
|
|
|
e−εt |
1) |
s |
ω2 |
−ε 2 |
, получаем: θ = − |
sinω t . Движение |
||
|
|
1 |
s |
|
|
1 |
|
|
|
|
|
|
|
|
ω1 |
периодическое, затухающее, период затухающих колебаний больше собственного
периода: T = |
|
|
|
2π |
|
|
. Логарифмический декремент затухания |
|||||||||
|
|
|
|
|
|
|
||||||||||
|
ω2 |
−ε 2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
an |
|
εT |
s |
|
πε |
|
|
|
πD1 |
|
|||||
Λ = ln |
= |
= |
|
|
= |
|
|
|||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
an+1 |
|
|
|
ω2 |
|
−ε 2 |
|
|
1− D2 |
||||||
|
|
|
|
|
|
|
|
s |
|
|
|
|
1 |
|
|
|
2) ωs < ε . Обозначим |
|
|
e−εt |
ε 2 −ωs2 |
= ν. Тогда θ = − |
shνt . Движение |
ν
апериодическое, затухающее, причем при малых t θ ≈ −te−εt , а при больших -
θ ≈ − exp((−ε +ν)t)
ν
Зная θ0 (t) для воздействия типа дельта-фунции, можно построить решение для произвольного воздействия u(t):
θ (t) = ∫t θ0 (t −τ )u(τ )dτ
0
3.2. Системы регистрации
Сейсмографы с прямой регистрацией
Механический способ. Этот способ использовался на самых ранних этапах развития сейсмологии. На конце маятника помещалось перо на расстоянии L от оси вращения (рис.3.3). Перемещение индикатора х связано с перемещением центра качаний хс
соотношением x = xc Ll , где l – приведенная длина маятника.
Рис.3.3. Механический способ регистрации
64
Соответственно увеличение прибора при этом равно
V = Ll
Регистрация производилась на закопченной бумаге, которая потом покрывалась специальным закрепляющим составом..
Однако, на маятник сейсмографа с механической регистрацией сильное влияние оказывает трение пера о бумагу. Чтобы уменьшить это влияние, необходима очень большая масса маятника. В одном из первых сейсмографов такой массой являлся бак, содержащий 17 т железной руды.
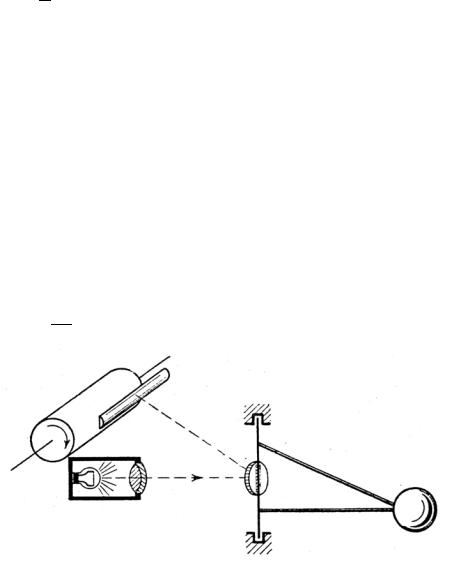
2) Оптический способ.
На оси вращения укрепляется зеркальце, которое освещается через объектив, отраженный луч попадает на фотобумагу, намотанную на вращающийся барабан (рис.3.4). Если длина оптического рычага А, то увеличение равно
V = 2lA
Рис.3.4. Оптический способ регистрации
Преобразователи механических колебаний
Преобразование механических колебаний в электрические может осуществляться разными способами. Долгое время в сейсмологии использовалась предложенная Голицыным гальванометрическая регистрации, основанная на
электродинамическом способе.
С маятником жестко скреплена индукционная катушка, которая помещается в поле постоянного магнита (рис.3.5). При колебаниях маятника магнитный поток меняется, в катушке возникает ЭДС, и ток регистрируется зеркальным
65
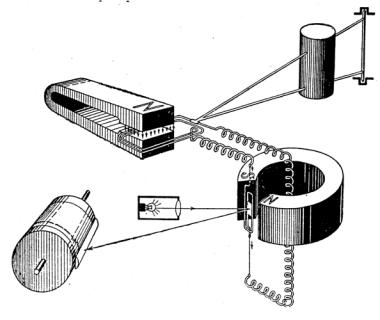
гальванометром. На зеркальце гальванометра направляется луч света, и отраженный луч, как и в оптическом способе, падает на фотобумагу.
Рис.3.5. Электродинамический способ регистрации
Но очевидно, что в таком способе мы регистрируем уже не движение центра качания маятника, а величину, связанную со скоростью колебаний, поскольку индуцируемый ток пропорционален скорости. Поэтому, если при прямой регистрации амплитудночастотная характеристика при больших периодах спадает как Т-2, то в случае, если регистрируется не смещение маятника, а его скорость, амплитудно-частотная характеристика будет спадать как Т-3 , что ограничивает регистрацию длиннопериодных колебаний.
Поэтому в последнее время получили распространение так называемые параметрические преобразователи. В этих преобразователях механическое перемещение (движение массы маятника) вызывает изменения какого-либо параметра электрической цепи (например, электрического сопротивления, емкости, индуктивности, светового потока, и т.п.). Изменение этого параметра приводит к изменению тока в цепи, и в этом случае именно смещение маятника (а не его скорость) определяют величину электрического сигнала. Из большого числа разнообразных параметрических преобразователей в сейсмометрии в основном используются два – фотоэлектрический и емкостной.
В фотоэлектрическом преобразователе движение массы маятника приводит к изменению светового потока, попадающего на светочувствительный элемент. На маятнике устанавливается легкая непрозрачная шторка, которая краем входит в световой поток, излучаемый любым источником света. За шторкой на пути потока
66
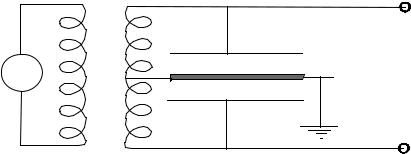
устанавливается светочувствительный элемент. Движение шторки приводит к изменению светового потока, и соответственно ток в цепи, содержащей фотоэлемент, пропорционален изменению попадающего на него потока.
Наибольшее распространение в сейсмометрии получил емкостной преобразователь Схема простейшего такого преобразователя, предложенного Беньоффом, изображена на рис. 3.6 .
~ |
P0 |
|
д о х вы
Рис.3.6. Схема емкостного преобразователя
Он состоит из двух идентичных катушек индуктивности L, замкнутых на сдвоенный конденсатор, средняя подвижная пластина которого Р0 заземлена и жестко связана с подвижной частью сейсмометра. Генератор постоянной частоты подает в образующиеся контуры контура напряжение с частотой близкой, но не равной их общей частоте. Когда средняя пластина конденсатора Р0 находится строго посередине между крайними обкладками, то контура сбалансированы, и сигнал на выходе преобразователя равен нулю. При смещении пластины Р0 из среднего положения один из контуров приблизится к своему резонансу, а другой уходит от него. При малом смещении пластины Р0 разбалансировка напряжений на выходе пропорциональна этому смещению.
Сейсмографы с обратной связью.
Линейная связь между колебаниями маятника и смещениями почвы имеет место только при малых колебаниях. То же относится и к связи между выходным напряжением (током) механоэлектрического преобразователя. Примером является изображенный на рис.3.6 емкостной преобразователь Беньоффа: линейная связь между смещением пластины Р0 и выходным напряжением имеет место только при малых отклонениях пластины от положения равновесия. Но в практике необходимо регистрировать как очень слабые движения почвы, так и достаточно сильные. При этом характеристика прибора должна быть одной и той же как в случае слабых, так достаточно сильных движений. Иначе говоря, динамический диапазон сейсмографа должен быть максимально широким. Для достижения этой цели в современных
67

преобразователях используют обратную связь. Принцип обратной связи заключается в следующем. Ускорение почвы воздействует на массу маятника, связанного с преобразователем смещений. В выходную цепь преобразователя включен контур обратной связи, ток в котором генерирует силу, компенсирующую входное ускорение, так что маятник почти не смещается из положения равновесия. Увеличение входного ускорения приводит к соответствующему увеличению тока в цепи обратной связи и соответственно к увеличению компенсирующей силы. Таким образом, подвижный элемент сейсмографа – маятник – в результате движения почвы остается практически неподвижным. А выходное напряжение будет определяться током обратной связи. При этом оказывается возможным также существенно расширить частотный диапазон регистрируемых колебаний
В сейсмографе Виланда-Штрекайзена STS-1, которым оборудованы многие станции глобальной сейсмической сети IRIS, динамический диапазон достигает 140 дБ, а амплитудно-частотная характеристика имеет столообразный вид в интервале периодов 0.1 с – 100 с.
Чтобы наблюдать движение почвы во всех направлениях, обычно используется три сейсмографа, - с вертикальным маятником и двумя горизонтальными, ориентированными на восток и на север. Однако, вертикальный и горизонтальный маятники различаются по своей конструкции, поэтому оказывается достаточно сложным добиться полной идентичности их частотных характеристик. Чтобы избежать этой трудности, в сейсмографе STS-2 все маятники ориентированы под одним и тем же углом к горизонту, так что они все являются идентичными. В каждом из приборов движение происходит в направлении ребер куба, поставленного на один из его углов (рис.3.7). Каждое из ребер наклонено по отношению к вертикали на угол 54.7°. Поскольку сейсмологи привыкли иметь дело с компонентами смещения в направлениях вверх, на север и на восток, смещения U,V,W пересчитываются в компоненты E,N,Z согласно соотношению
E |
|
|
|
|
− 2 1 |
1 U |
||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
N |
= |
|
|
|
|
0 |
|
|
3 |
|
− 3 |
|
|
|||||
|
|
|
|
|
|
|||||||||||||
6 |
|
|
|
|
|
V |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Z |
|
|
|
|
2 |
|
2 |
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
W |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку запись производится в цифровом коде, такой пересчет осуществляется непосредственно в самом приборе, и на выходе мы получаем компоненты E,N,Z .
68
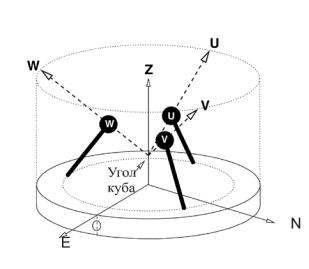
Рис.3.7. Ориентация регистрируемых компонент смещения в сейсмографе STS-2/
Во всех современных системах регистрации производится преобразование механических колебаний в электрические с помощью тех или иных преобразователей. Входным сигналом является смещение почвы, а выходным – ток или напряжение на выходе системы. В задачах сейсмологии требуется с достаточной точностью знать именно сигнал на входе. Входной сигнал может быть достаточно точно оценен, если известна частотная характеристика системы. Она определяется следующим образом. Поскольку колебания малы, то система является линейной, и в общем (в зависимости от преобразователя) уравнение, связывающее входной сигнал x(t) и выходной y(t) имеет вид:
ao y(n) + a1 y(n−1) +.... + an−1 y′ +an y = −Bx(k )
где к=2 или 3 в зависимости от того, используется ли преобразователь по смещению или по скорости. Обычно вместо того, чтобы определять характеристику
|
|
S(ω) = |
|
|
− B(iω)k |
|
|
|
|
|
|
|
|
|
||
|
|
a |
0 |
(iω)n + a (iω)n−1 |
+...a |
n |
|
|
|
|
|
|||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
разлагают знаменатель на множители: |
|
|
|
|
|
|||||||||||
a |
0 |
(iω)n + a |
(iω)n−1 +...a |
n |
= a |
0 |
(s − z |
)(s − z |
2 |
)...(s − z |
n |
) |
||||
|
1 |
|
|
|
1 |
|
|
|
||||||||
и определяют характеристику значениями полюсов z1 , z2 ..., и количеством "нулей" в числителе (2 или 3) и величиной постоянного множителя B / a0
("увеличение"). Набор этих чисел полностью описывает частотную характеристику и является как бы «паспортом» прибора. Этот набор входит в стандартный код цифровой записи на каждой станции. Он используется для корректировки записи за характеристику прибора.
69
3.3. Сейсмический шум
Даже в периоды отсутствия сейсмических событий на сейсмограммах всегда присутствуют колебания, называемые микросейсмами. Они являются помехой для сигналов, вызываемых землетрясениями. Поэтому в задачу сейсмометрии входит еще и снижение сейсмического шума.
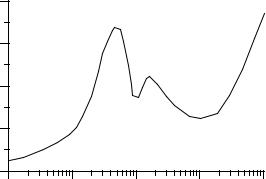
Микросейсмы возникают за счет различных источников (ветер, перепады атмосферного давления, штормы в океане, вариации температуры, движение транспорта и т.п.). Интенсивность микросейсм различна на разных станциях в зависимости от их местоположения и грунтовых условий и имеет сезонные и суточные вариации. Кроме пространственной и временной неравномерности микросейсмы характеризуются и неравномерностью распределения интенсивности с частотой, что обусловлено различием вызывающих их причин. Хотя зависимость интенсивности микросейсм от частоты разная на разных станциях, она имеет общие для всех станций характерные особенности, а именно, наличие отчетливого максимума на частоте около 0.15 Гц, менее выразительного максимума на частоте ~ 0.07Гц, минимума в интервале 0.002-0.03 Гц и повышения интенсивности с уменьшением частоты. Спектр шума имеет разный вид в зависимости от того, рассматривается ли смещение, скорость или ускорение. Схематически спектр мощности шума по отношению к скорости колебаний изображен на рис. 3. 8.
|
-100 |
|
|
|
|
(м/с)2/Гц |
-120 |
|
|
|
|
-140 |
|
|
|
|
|
|
|
|
|
|
|
dB |
-160 |
|
|
|
|
|
|
|
|
|
|
|
-180 |
|
|
|
|
|
0.1 |
1 |
10 |
100 |
1000 |
|
|
|
период, с |
|
|
Рис. 3.8. Типичный вид спектра сейсмического шума.
Максимум спектра на периоде ~ 5-7с и менее выраженный максимум на периоде около 15 с обусловлены циклонической обстановкой в океане. Соответствующие колебания получили поэтому название штормовых микросейсм. Их интенсивность велика на станциях, расположенных вблизи берега, и очень мала в центральных частях континентов. Интенсивность штормовых микросейсм резко возрастает в периоды штормов в океане. Штормовые микросейсмы образованы главным образом волнами Релея, но частично могут содержать и волны Лява. Период ветровых волн составляет 10-15 с, так что соответствующий период в спектре обусловлен действием
прибойных волн на берег. А вдвое меньший период, которому соответствуют более
70
интенсивные колебания, объясняется образованием в океане стоячих волн в результате интерференции волн, распространяющихся в противоположных направлениях (к центру циклона). При этом гидродинамическое давление на дно одинаково как при поднятии воды, так и при опускании, поскольку оно пропорционально квадрату скорости жидкости. Соответственно оно меняется с периодом вдвое меньшим, чем скорость водных волн. При этом оно синхронно меняется на всей территории, где образуются стоячие волны. Эти колебания давления приводят к образованию упругих волн в дне, которые, распространяясь по направлению к континенту, и создают интенсивные микросейсмы с периодами 5-7 с. При распространении вглубь континента штормовые микросейсмы затухают, поэтому их интенсивность мала на станциях, расположенных вдали от берега.
Короткопериодные микросейсмы (с периодами менее 2 с) вызываются локальными источниками (работа промышленных установок, транспорт, ветер, водопады). Они содержат как поверхностные, так и объемные волны. В близких точках короткопериодный шум некогерентен. Этот шум уменьшается с глубиной.
Длиннопериодные микросейсмы с периодами более 30 с являются результатом ряда факторов, основными из которых считаются вариации атмосферного давления, ветер, изменение давления на дно океана вследствие приливов.
Очевидно, что для регистрации волн от землетрясений необходимо добиваться по возможности снижения интенсивности шума. Это осуществляется установкой станций на выходах скальных пород, заглублением приборов, удалением станций от береговой линии. Поскольку грунтовые условия часто неизвестны, при выборе места для станции необходимо предварительное измерение шума в разных пунктах территории, где планируется установка станции.
Литература к главе 3.
Саваренский Е.Ф. и Кирнос Д.П. Элементы сейсмологии и сейсмометрии. Гостехиздат. М., 1955. 543 с.
Рыков А.В.Моделирование сейсмометра. М.,ОИФЗ РАН, 1996. 108 с.
Wieland E. and Streckeisen. The leaf-spring seismometer; Design and performance. Bull.Seism.Soc.Am., 72(6), 1982. 2349-2367.
Wieland E. Seismometry. In: International Handbook of Earthquake and Engeneering Seismology. Acad.Press. London. 2002. p.283-304.
F.Scherbaum. Of poles and zeros. Modern approaches in Geophysics, v.15. Kluwer Acad.Press, 1996. 256 p.
71
Дж.А.Эйби. Землетрясения. 1982. М.Недра. 264 с.
К.Е.Буллен. Введение в теоретическую сейсмологию. 1966. М.Мир. 460 с.
72
Глава 4. Волны в Земле и их записи на сейсмограммах
4.1. Основные определения
Область, где возникают pазpушения и наблюдаются остаточные дефоpмации, называется очагом или гипоцентpом землетpясения. Пpоекция очага на повеpхность Земли называется эпицентpом.
Момент возникновения землетpясения называется вpеменем в очаге.
Pасстояние от эпицентpа до точки наблюдения на земной повеpхности называется эпицентpальным pасстоянием. Эпицентpальное pасстояние измеpяется в км или гpадусах дуги большого кpуга.
Землетpясения, заpегистpиpованные на pасстоянии менее 1000 км от эпицентpа, называются близкими, на больших pасстояниях - удаленными. Близкие и удаленные землетpясения pазличаются по хаpактеpу волнового поля, pегистpиpуемого на земной повеpхности. На близких расстояниях регистрируются волны, распространяющиеся в верхних отделах Земли – коре и верхах мантии. Волны от удаленных землетрясений проникают в глубокие части Земли – мантию и ядро.
Зависимость времени пробега волны от эпицентрального расстояния называется
годографом.
4.2. Номенклатура волн в Земле
Близкие землетрясения.
На расстояниях менее 1000 км Землю можно в первом приближении считать плоской, земную кору представлять в виде слоя или нескольких слоев, в которых скорости сейсмических волн меньше, чем в нижележащей мантии. Основные волны, распространяющиеся в такой структуре – это прямые продольные и поперечные – их
обозначают P, S или Pg , Sg , и преломленные в мантию (Pn , Sn ) и
распространяющиеся в ней приблизительно вдоль границы, проникая в мантию на небольшую глубину. На очень малых расстояниях приходят только прямые волны. Преломленные волны выходят на поверхность Земли начиная с расстояния, соответствующего критическому углу падения волны на границу кора-мантия. Вначале они приходят позже прямых, но начиная с расстояния около 200 км обгоняют их и приходят в первых вступлениях. С удалением от эпицентра прямые волны
постепенно затухают, а Pn , Sn остаются. Помимо фаз Pg , Sg , Pn , Sn на сейсмограммах
выделяются иногда дополнительные фазы – их обозначают P* , S* , которые
идентифицируются с волнами, преломленными на промежуточной границе в коре. На рис.4.1а представлены схематически волны в простейшей однослойной модели коры.
Pg
Pn
Рис.4.1. Схема распространения основных волн в коре
73
Удаленные землетрясения.
На больших расстояниях приходят волны, проникающие на большие глубины, отражающиеся от границ и проходящие через основные структурные элементы Земли
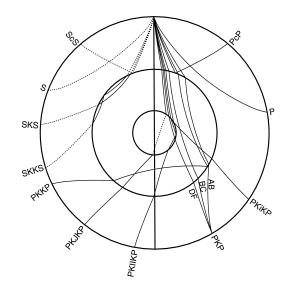
– мантию (до глубины 2900 км), жидкое (внешнее) ядро (от 2900 до 5150 км) и внутреннее ядро. Волны отражаются и преломляются на границах между мантией и внешним ядром и между внешним и внутренним ядром, а также отражаются от свободной поверхности Земли. При этом, как было показано в главе 2, при падении на границу продольной Р волны образуются отраженные и преломленные Р и SV волны. Через жидкое ядро поперечные волны не проходят. Источник излучает и продольные, и поперечные волны, и каждая из них претерпевает отражение-преломление на границах. Поэтому общее возможное число образующихся волн будет достаточно большим.
На рис.4.2 схематически изображены трассы основных волн в Земле от источника на поверхности с указанием их обозначений. Волны, проходящие через мантию, обозначаются Р,S. Если такая волна отразилась от свободной поверхности, - при этом возникают как продольные, так и поперечные волны, - то такие волны обозначаются соответственно РР, SS, SP, PS. При следующем отражении одной из этих волн снова образуются отраженные продольные и поперечные волны, обозначаемые как РРР,
SSS, PPS, SPP и т.д. - каждое звено луча такой волны обозначается соответствующим символом.
Рис.4.2. Схема распространения основных волн в Земле
Отражение от границы ядра обозначается буквой с (core), так что волна, вышедшая из источника как продольная и отразившаяся от границы ядра тоже как продольная будет иметь обозначение РсР. Аналогично отраженная поперечная волна обозначается как ScS. Очевидно, что возможны также волны PcS, ScP. Буква K используется для обозначения продольной волны, прошедшей через жидкое ядро, так что волна, вышедшая из источника как продольная, преломившаяся в ядро и вышедшая в мантию снова как продольная будет иметь обозначение PKP. Легко теперь понять, что обозначают символы SKS, PKS, SKP. Если волна, прошедшая в жидкое ядро, отразится от границы ядро-мантия снизу , будет продолжать распространяться в жидком ядре, и
74
при следующем падении ее на границу преломится в мантию, то такая волна будет обозначена как PKKP, и т.п. Волна, пересекающая твердое внутреннее ядро, обозначается буквой I (от слова inner core) , так что волна, прошедшая весь путь через мантию, внешнее и внутреннее ядро как продольная, будет иметь обозначение PKIKP. Отражение от внутреннего ядра обозначается малой буквой i . Так PKiKP представляет волну, прошедшую как продольную через мантию, далее через жидкое внешнее ядро и отразившуюся от границы внутреннего ядра.
Исходя из этой символики, можно обозначать любые сложные фазы. Например, PcPPKР – это продольная волна, отразившаяся от ядра, затем отразившаяся от поверхности Земли и прошедшая через внешнее ядро. Конечно, не все такие волны видны на сейсмограммах – амплитуды некоторых волн, особенно испытавших несколько отражений/преломлений, очень малы и не могут быть выделены на фоне предшествующих им более интенсивных волн.
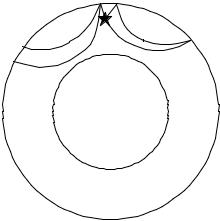
Дополнительные фазы появляются от глубокофокусных землетрясений. Их появление обусловлено тем, что волна (Р или S) выходит еще и вверх из источника и отражается от поверхности Земли. Звено луча на пути о от агач до поверхности обозначается малыми буквами p или s. Так, волна, вышедшая из источника как поперечная, отразившаяся над источником и превратившаяся после отражения в продольную, будет обозначена как sP. На рис.4.3 изображены пути волн от глубокофокусного источника и прошедшие через мантию. Для простоты здесь не показаны волны, образовавшиеся на границах мантия-ядро и внутри ядра.
|
p |
|
P |
P |
|
s |
P |
|
s |
||
|
||
S |
|
Рис.4.3. Схема волн от глубокофокусного источника
Кроме объемных (продольных и поперечных) волн землетрясения возбуждают еще и поверхностные волны – Релея и Лява. Поскольку в земной коре и в верхней мантии скорости сейсмических волн изменяются с глубиной – в среднем они с глубиной возрастают – эти волны характеризуются дисперсией скорости – волны с разными периодами распространяются с разными скоростями. Это приводит к тому, что излучаемый источником импульс, содержащий широкий спектр частот, растягивается во времени, причем тем больше, чем большее расстояние проходит волна.
75

4.3. Годографы
Близкие землетрясения
В случае близких землетрясений кору можно считать плоским слоем мощностью Н. В первом приближении скорость сейсмической волны в слое (как продольной, так и поперечной) можно считать постоянной, равной V1 , скорость ниже границы коры будем обозначать V2 . Если очаг находится на глубине h, то
время распространения прямой волны ( Pg или Sg ) от очага до пункта
наблюдения, находящегося на эпицентральном расстоянии Х, может быть определено по формуле
T = |
|
X 2 |
+ h2 |
|
|
V1 |
|
||
|
|
|
||
Годограф этой волны – гипербола. На больших расстояниях (Х>>h) она становится близкой к прямой линии, наклон которой определяется скоростью в
слое. |
|
|
|
|
|
|
|
|
|
мантию волны (Pn или |
S n) |
|
Время распространения |
преломленной в |
|||||||||||
определяется следующим образом: |
|
|
|
|||||||||
T = t |
|
+ |
X |
где |
t |
|
= |
2H − h |
cosθ , |
θ = arcsin |
V1 . |
|
|
0 |
|
|
|||||||||
|
|
|
||||||||||
|
0 |
V |
|
|
|
V1 |
|
V |
|
|||
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
Эта волна появляется на расстоянии X 0 = (2H − h) tanθ . Таким образом годограф
этой волны представляет собой прямую линию, наклон которой определяет скорость в подстилающей среде.
Годографы прямой и преломленной волн изображены на рис.4.4.
T |
|
|
Pn |
|
Pg |
X0 |
X |
Рис.4.4 Годографы продольных волн в коре |
|
Удаленные землетрясения
Годографы волн от удаленных землетрясений приведены на рис.4.5. Эти годографы были построены путем кропотливого анализа записей землетрясений на протяжении нескольких десятков лет. Очевидно, что для построения годографа необходимо достаточно точно знать координаты очага и время в очаге. Но эти параметры в свою очередь могут быть определены на основе знания годографа.
76
77
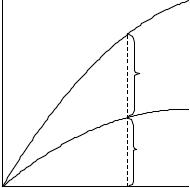
Рис.4.5 Годографы волн от удаленных землетрясений
Первые, очень грубые таблицы времен пробега Р и S волн были составлены Цёппритцом в 1907 году. Он собрал все доступные данные о трех землетрясениях, эпицентры которых были известны по степени разрушений (Индия,1905 г., Калабрия, 1905 г. и Калифорния 1906 г.), и которые были зарегистрированы
многими станциями на расстояниях от 1° до 100°, и свел имеющиеся данные в таблицы. Этими таблицами пользовались для определения координат очагов вплоть до 1929 года, когда Джеффрис и Буллен произвели пересмотр этих таблиц на основе статистического анализа полученных к тому времени наблюдений. Таблицы времен пробега уточнялись методом последовательных приближений. При этом использовалась большая совокупность данных о временах прихода волн (на разных станциях и от разных землетрясений) и методом наименьших квадратов оценивались поправки к координатам и времени в очагах и к таблицам времен пробега. . По наблюдениям определялись только годографы основных фаз: Р, S,PKP, PKIKP, а годографы остальных волн определялись путем расчетов. Джеффрис и Буллен опубликовали новые таблицы в 1935 году, и они долгое время использовались в сейсмологической практике для определения параметров очагов землетрясений. В дальнейшем, по мере накопления наблюдений эти таблицы неоднократно подвергались пересмотру, но оказалось, что поправки к таблицам Джеффриса-Буллена достаточно малы.
Первое время координаты очагов определялись по годографам Р и S следующим образом. По сейсмограммам определялась разность вступлений фаз Р и S. По
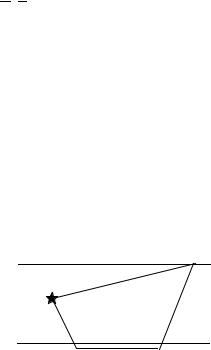
годографам Р и S волн можно было определить расстояние ∆, на котором разность прихода этих волн равна наблюдаемой (рис.4.6).
Для этого расстояния по годографу Р- волны можно было определить время ее
пробега от очага до станции TP (∆) , и тем
самым |
определить |
время в очаге |
||||
t |
0 |
= tнабл −T |
P |
(∆) . Зная |
эпицентральные |
|
|
P |
|
|
|
||
расстояния на нескольких станциях, можно было определить и положение эпицентра.
t |
|
S |
|
|
tP-tS |
P |
|
|
TP |
∆ |
∆ |
|
Рис.4.6. Определение эпицентрального расстояния и времени в очаге по годографам волн Р и S
Такой способ использовался долгое время, пока обработка сейсмических наблюдений производилась вручную. В случае, когда очаг находился на некоторой глубине, сначала оценивалась глубина очага h по разности времен прихода фаз рР и Р (или sР и
Р) , а затем эпицентральное расстояние оценивалось по годографам TP (∆, h) и
TS (∆, h) .
Однако, способ, требующий измерения времен прихода не только волн Р, но и S, (а в случае глубоких очагов еще и рР или sP) приводил к значительным погрешностям в определении параметров очагов, потому что волна S (так же, как рР и sP ) приходит на фоне других волн, вследствие чего выделение ее вступления на сейсмограммах затруднительно, соответственно время вступления волны S определяется с ошибкой, значительно большей, чем ошибка в определении времени вступления волны Р. Но с
78
появлением вычислительных машин и внедрения их в практику сейсмологической обработки стало возможным использовать для определения параметров очагов только
данные о временах вступлений волн Р. Если известен годограф TP (∆, h) волны Р и на ряде станций определены времена вступлений Р-волны tP(i) , то из системы уравнений
t(i) = T |
P |
(∆ |
, h) + t |
0 |
(i=1,2,..n) |
P |
i |
|
|
где cos ∆i = sinϕi sinϕ0 + cosϕi cosϕ0 cos(λi − λ0 ) , ϕi , λi - широта и долгота станции, методом наименьших квадратов могут быть определены координаты эпицентра ϕ0 , λ0 ,
глубина очага h и время в очаге t0.
4.4. Сейсмограммы
Близкие землетрясения
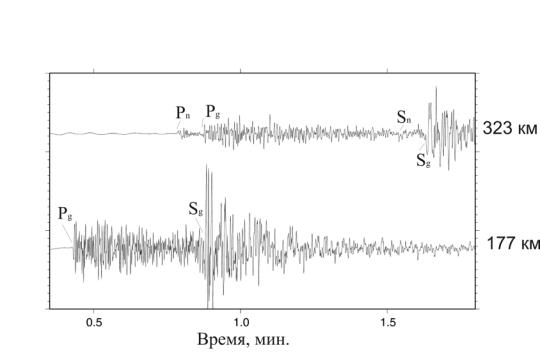
Как уже отмечалось в разделе 4.2, на записях близких землетрясений регистрируются волны прямые (Рg, Sg) и преломленные (Рn, Sn). В зависимости от эпицентрального расстояния порядок прихода этих волн меняется. На малых расстояниях первыми приходят волны Рg, Sg, при этом волны Рn, Sn часто бывает трудно выделить из-за их малой интенсивности. На расстояниях более ~200 км в первые вступления выходят волны Рn, Sn . Продольные волны отчетливее видны на записи вертикальной компоненты, тогда как поперечные волны более выразительны на записях горизонтальных компонент. Примеры записей на расстояниях 177 км и 323 км приведены на рис.4.7.
Рис.4.7. Примеры сейсмограмм от близких землетрясений. На расстоянии 177 км первыми вступают волны Рg, Sg , более слабые волны Рn, Sn не видны на их фоне. На расстоянии 323 км в первые вступления уже приходят волны Рn, Sn, и на сейсмограмме отчетливо видны по два вступления продольных и поперечных волн
79
На рис.4.8 изображена запись землетрясения 29.05.1999 с глубиной очага 10 км, записанного на шведской станции Уддехольм на расстоянии 530 км от очага. Кроме волн Рg, Sg , Рn, Sn на записи выделяется продолжительное колебание после волны Sg , которое представляет собой поверхностную волну, образованную в верхних слоях коры. Эту волну обозначают Lg .
Рис.4.8. Пример сейсмограммы землетрясения на расстоянии 530 км от очага. Продолжительное колебание после волны Sg обусловлено поверхностными волнами в верхних слоях коры (Lg ).
Удаленные землетрясения
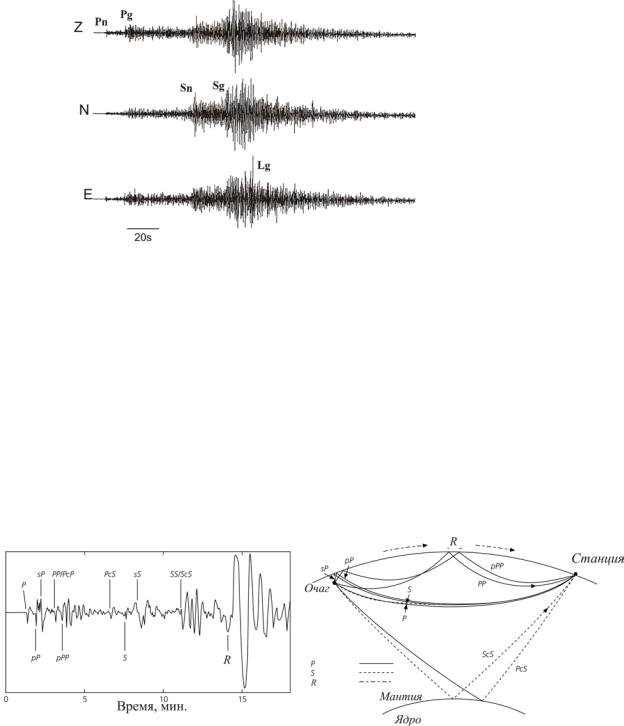
На рис.4.9 приведена сейсмограмма землетрясения с глубиной очага 150 км на
расстоянии 43.5° (вертикальная компонента смещения) и изображены трассы волн, выделенных на сейсмограмме. Чтобы не загромождать рисунок, на нем не показан луч волны РсР , так как он совпадает с лучом ScS, а также луч волны SS, совпадающий с лучом РР. Символом R обозначена поверхностная волна Релея. Символы остальных волн объяснены в разделе 4.2.
Рис.4.9. Слева сейсмограмма на расстоянии 43,5°, справа – схема соответствующих волн в мантии
80
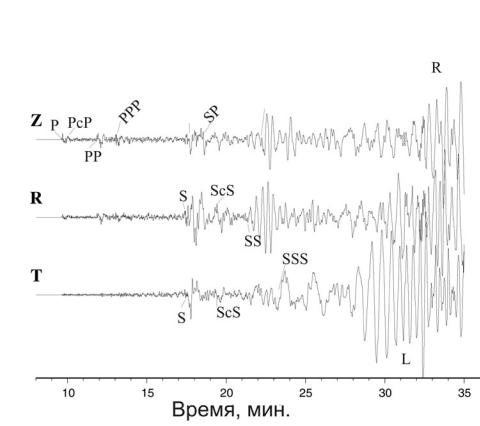
На рис.4.10а,б приведены трехкомпонентные записи землетрясения на Тайване, полученные
на станциях ABKT и ESC на расстояниях соответственно 55° и 88°. Вертикальная компонента обозначена Z, горизонтальные компоненты – R (радиальная) и Т (трансверсальная).
а
б
81
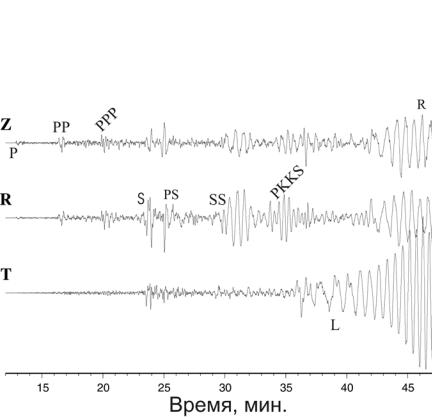
Рис.4.10. Примеры сейсмограмм на расстояниях 55° (а) и 88° (б)
На рис.4.11 приведена сейсмограмма глубокофокусного землетрясения с глубиной очага 459 км. При такой глубине очага отчетливо выделяются волны, отраженные от земной поверхности над очагом (рР, sS, sP). Записи глубокофокусных землетрясений, как правило, более высокочастотные, и импульсы в них более короткие. Это облегчает выделение отдельных фаз.
82
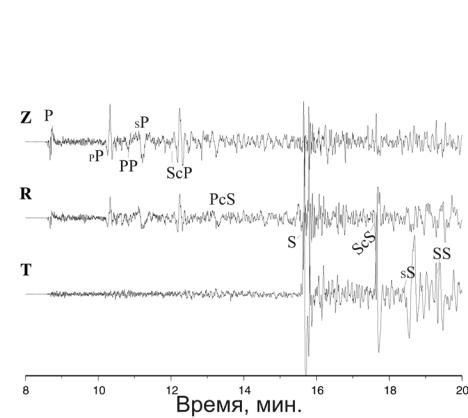
Рис.4.11. Пример сейсмограммы глубокофокусного землетрясения на эпицентральном расстоянии 53°.
Литература к главе 4.
Kulhanek O. Anatomy of Seismograms. Elsevier Science. Amsterdam. 1990. 178 p.
Kulhanek O. The structure and interpretation of seismograms. . In: International Handbook of Earthquake and Engeneering Seismology. Acad.Press. London. 2002. p.333-348.
Джеффрис Г. Земля, ее происхождение, история и строение. Изд-во иностранной1 литературы. М. 1960. 484 с.
Дж.А.Эйби. Землетрясения. 1982. М.Недра. 264 с.
Дж.Ходжсон. Землетрясения и строение Земли. М.Мир.,1966. 193 с.
Ф.Стейси. Физика Земли. М.Мир., 1972., 342 с.
H.Jeffreys, K.E.Bullen. Seismological Tables. 1968.
Kennett B.L.N. Seismic Traveltime Tables. In: A Handbook of Physical Constants. Global Earth Physics, AGU Ref.Shelf 1, (ed.T.Ahrens), p.126-143. 1995, (http://www.agu.org/reference/gephys/10_kennet.pdf)
Kennett B.L.N. Seismological Tables: ak135. Research .School of Earth Sci., Australia National Univ., Canberra, 2005, 289 p. (http://www.iaspei.org/downloads/AK135tables.pdf)
83
Глава 5. Энергия и механизм землетрясений.
5.1 Энергия и магнитуда
Энергия, выделяемая пpи землетpясении, пеpеходит в тепловую, энеpгию пластических дефоpмаций, и только небольшая ее доля переходит в в энеpгию сейсмических волн. Но поскольку эта энеpгия является опpеделенной частью полной энеpгии землетpясения, ее можно использовать как хаpактеpистику энеpгии землетpясения.
Pассмотpим, как можно пpиближенно оценить энеpгию излучаемой очагом сейсмической волны.
Обозначим энергию упругой волны (продольной или поперечной), излучаемой источником, через Е. Предположим, что источник излучает равномерно во всех направлениях. В действительности такое может иметь место только в случае продольной волны, излучаемой источником типа центр расширения. В этом случае в одноpодной сpеде поток энеpгии упpугой объемной волны через единицу поверхности на pасстоянии r от источника pавен
Er = |
E |
|
e−kr |
(5.1) |
4πr |
2 |
|||
|
|
|
|
В этой формуле член 4πr 2 определяет геометрическое расхождение волны, а экспоненциальный множитель – затухание волны вследствие поглощения.
Соответственно E = 4πr 2 Er ekr . А величину Er можно определить по характеристикам волны на расстоянии r.
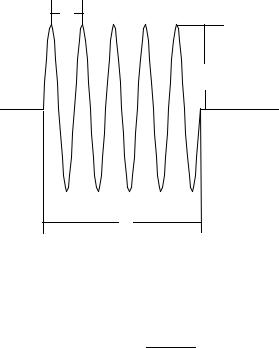
Выражение для потока энергии волны за некоторый промежуток времени дается формулой (2.45). Если движение в волне пpедставляет цуг гаpмонических колебаний с пеpиодом Т , одной и той же амплитудой А и длительностью t0 (рис.5.1) то
u = Asin |
2πt |
, |
|
= |
2πA |
cos |
2πt |
, |
P = |
4π 2 |
A2 |
t0 |
2 |
2πt |
dt |
||
|
T |
u |
T |
|
T |
T |
2 |
ρc∫cos |
|
T |
|||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|||||
< T > |
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
< |
t0 |
> |
Рис.5.1. Вид волнового цуга
2π
Учитывая, что ∫cos2 xdx = π , мы получим
0
Er = P = 2πT22A2 ρct0
84
Соответственно энеpгия источника pавна
E = |
8π 3 |
A2 |
ρcr 2 ekr t |
|
(5.2а) |
|
T |
2 |
0 |
||||
|
|
|
Если амплитуда и пеpиод колебаний изменяются во вpемени, то это выpажение приближенно можно заменить интегpалом
t0 |
|
E = 8π 3 ρcr 2 ekr ∫( A / T)2 dt |
(5.2б) |
0 |
|
В действительности волны pаспpостpаняются не в одноpодной сpеде, так что энеpгия pаспpеделяется не pавномеpно по сфеpе pадиуса r, а в зависимости от pасхождения лучей. Но если известно pаспpеделение скоpости в сpеде это pасхождение можно вычислить и подставить в фоpмулу (5.2) вместо r2.
Аналогично можно оценить и энеpгию повеpхностных волн. Для простоты рассмотрим релеевскую волну в однородном полупространстве. Как было показано в разделе 2.11, движение в волне Релея происходит по эллипсу в вертикальной плоскости, так что волна имеет две компоненты – вертикальную w и горизонтальную в направлении
распространения волны u . Эти компоненты сдвинуты по фазе на π/2 , имеют максимальные значения на поверхности и затухают с глубиной. Энергия поверхностной волны переносится через поверхность полубесконечного цилиндра радиуса r . Плотность энергии волны в соответствии с формулой (2.44) в этом случае имеет вид
W (z, r,t) = ρ( |
|
|
|
2 |
+ |
|
|
(z, r,t) |
|
2 |
) |
||
|
|
|
|
||||||||||
|
w(z, r,t) |
|
|
|
u |
|
|
||||||
Поток энергии, переносимый волной |
через цилиндрическую поверхность за время, |
||||||||||||
равное одному периоду, |
будет очевидно равен |
|
|||||||||||
T |
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E = ∫ |
2πr∫W (z, r,t)dz cdt |
|
|
|
|
|
|
|
|
|
|||
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку наблюдения проводятся на поверхности, эту величину следует выразить через амплитуду волны на поверхности. При этом обычно для оценки энергии поверхностной волны используется горизонтальная компонента смещения U = u(0) .
Выразим энергию поверхностной волны Е через значение амплитуды горизонтальной составляющей смещения на поверхности. Компоненты смещения u и w в волне с плоским фронтом выражаются с точностью до постоянного множителя С формулой
(2.52), а в случае |
сосредоточенного источника в эти выражения должен быть добавлен |
|||||
множитель |
|
1 |
|
|
за счет геометрического расхождения волны. Учитывая также, что |
|
|
|
|
|
|||
2πr |
||||||
|
|
|
||||
T∫sin2 ωtdt = T∫cos2 ωtdt = |
T |
|
|
|
|
||||
0 |
0 |
|
|
|
2 |
|
|
|
|
и интегрируя по z, мы получим |
|
|
|
|
|||||
|
|
|
|
2 |
|
2 |
|
|
c |
E = 1 |
ρω2cTC2 |
β(1 +α |
|
) + α(1+ β ) − 2 |
|
||||
|
|
||||||||
|
|
αβ |
|||||||
|
|
|
|||||||
2 |
|
|
2α |
|
2β |
|
|
|
ω |
|
|
|
|
|
|
||||
Амплитуда горизонтальной составляющей смещения на поверхности z=0 и на расстоянии r от источника , согласно формуле (2.52), равна
U = C
 β (1−
β (1− 
 αβ )/
αβ )/ 
 2πr
2πr
откуда
C = |
|
U |
2πr |
|
|
|||
|
|
|
|
|
|
|
||
β (1− αβ ) |
||||||||
|
|
|||||||
и, учитывая, что ωT = 2π ,
85
|
|
β(1 +α2 ) |
|
α(1 + β 2 ) |
− 2 |
|
|
|
|||
|
|
+ |
αβ |
||||||||
E = 2π 2 ρc2rU 2 |
|
2α |
|
2β |
|||||||
|
|
|
|
|
(5.3) |
||||||
|
|
|
|
|
|
|
|
|
|||
|
β(1 − αβ )2 |
|
|||||||||
|
|
|
|
|
|
|
|||||
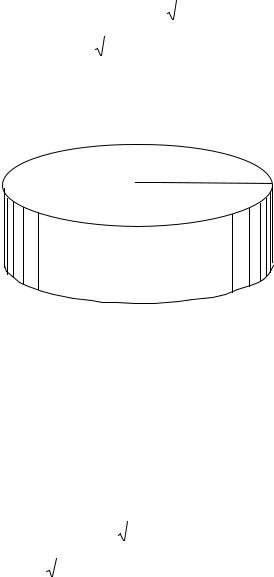
Если условно принять, что энергия волны с постоянной амплитудой U переносится через поверхность цилиндра с радиусом r и высотой Н (рис.5.2), то
E = 2π 2 ρcrHωU 2 |
(5.4) |
r
H
Рис.5.2 . Схематическое изображение цилиндрической поверхности, через которую переносится энергия релеевской волны.
Сравнивая (5.3) с (5.4), мы можем определить толщину эквивалентного близповерхностного слоя, в котором была бы сосредоточена энергия поверхностной волны, если бы она имела по всей толщине Н одинаковую амплитуду, равную амплитуде горизонтального смещения на поверхности:
|
|
β(1+α 2 ) |
|
α(1+ β 2 ) |
|
|
|
|
|
||
|
|
+ |
− 2 αβ |
|
|
λ |
|||||
H = |
|
2α |
2β |
|
|
||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
2π |
|
β(1− αβ )2 |
|
|
|
|
|||||||
|
|
|
|
|
|
||||||
где λ - длина волны. Для среды Пуассона (σ=1/4) оказывается, что H ≈1.1λ .
Это соотношение будет несколько отличаться в случае вертикально-неоднородной среды и в случае, когда поверхностная волна образована волнами Лява, но обычно принимают, что энергия поверхностной волны сосредоточена в слое толщиной равной длине волны.
Как уже упоминалось в главе 2, в реальных вертикально-неоднородных средах поверхностные волны характеризуются дисперсией скорости, так что волновой цуг представляет собой колебания с изменяющейся во времени частотой (глава 4, рис. 4.9, 4.10). Поэтому при вычислении полного потока энергии следует учесть зависимость амплитуды, периода, скорости и соответственно длины волны от времени. Таким образом, выражение для потока энергии в поверхностной волне за время t0 запишется в виде
t0 |
|
E = 4π 3 ρr∫(A /T )2 cλdt |
(5.5) |
0 |
|
В этойфо рмуле в качестве с |
должна быть взята групповая скорость. Если еще учесть |
затухание волны вследствие поглощения, тогда в подынтегральное выражение добавится множитель exp(kr) .
Измеpение энергии по пpиведенным фоpмулам неудобно: надо измеpять все пеpиоды и амплитуды в волновом цуге, и еще вводить сложный коэффициент. Кpоме того, величина
86
энеpгии неудобна в качестве хаpактеpистики, так как она варьирует в очень шиpоком диапазоне - в пpеделах по кpайней меpе 10-15 поpядков. Поэтому было удобнее ввести величину, связанную с поpядком энеpгии, пpичем так, чтобы ее было легко измеpять, пусть даже достаточно приближенно. Так было введено понятие магнитуды.
Впеpвые понятие магнитуды было введено Pихтеpом в 1935 г. для сpавнительной оценки силы калифоpнийских землетpясений на близких (до 600 км) станциях. Магнитуда опpеделялась как десятичный логаpифм максимальной амплитуды, измеpяемой в микpонах, записанной стандаpтным коpоткопеpиодным сейсмогpафом Вуда-Андерсона на pасстоянии 100 км от эпицентpа. В случае близких землетрясений в волновом пакете бывает трудно выделить отдельные волны, поэтому Рихтером и было принята оценка силы землетрясения просто на основе максимальной амплитуды колебаний, которая обычно находилась в цуге волн S. В настоящее время определяемую таким способом магнитуду называют локальной магнитудой ML. Как следует из определения,
M L = log10 A + f (∆)
Рихтер определил функцию f (∆) эмпирически, причем так, чтобы f (100) = 0 . Поскольку
в настоящее время только на небольшом числе станций сохранилась регистрация с помощью сейсмографа Вуда-Андерсона, запись, полученную сейсмографом с другой частотной характеристикой, можно преобразовать к такой, которая отвечает сейсмографу Вуда-Андерсона.
В1945 г. Гутенбергом определение магнитуды было расширено таким образом, что для
ееоценки стало возможным использовать как объемные, так и поверхностные волны,
зарегистрированные любым калиброванным сейсмографом и на любомэ пицентральном расстоянии.
Надо заметить, что оценка энергии землетрясения по величине энергии упругих волн зависит от того, какие волны используются для этой цели, поскольку энергия каждой из волн – продольной, поперечной, поверхностной – составляет определенную долю полной выделившейся энергии, причем разную в разных случаях. Соответственно и магнитуда как оценка сейсмической энергии будет разной, в зависимости от того, какие используются волны. Правда, это различие будет не очень велико, поскольку доля полной сейсмической энергии в каждой из волн будет примерно одна и та же.
Как видно из формул (5.2) и (5.5) энергия пропорциональна квадрату скорости
колебаний, или отношению A2 / T 2 . Эта величина меняется в пределах волнового цуга, но можно принять, что суммарное ее значение по временному интервалу приблизительно пропорционально максимальному значению. Поэтому для сравнения силы землетрясений
естественно принимать величину |
|
A |
, отнесенную к какому-то фиксированному |
|
log |
|
|
||
|
||||
|
T max |
|
||
эпицентральному расстоянию. При этом корректировка за эпицентральное расстояние была осуществлена так, чтобы получающееся значение магнитуды было согласовано с тем, которое отвечает шкале Рихтера.
Опpеделение магнитуды по объемным волнам. Так как энеpгия волн пpопоpциональна
A2/T2, то в качестве хаpактеpистики энеpгии (магнитуды) стали пpинимать величину
m |
|
= log |
|
A(∆) |
+ Q |
(∆, h) |
|
|
|
|
|
||||
|
|
||||||
|
b |
10 |
T (∆) max |
b |
|
||
где амплитуда А выражена в микpонах, а период Т - в секундах; h глубина очага.
Калибpовочная функция Qb(∆,h) учитывает геометpическое pасхождение волны и затухание вследствие поглощения. Эта функция опpеделялась эмпиpически так, чтобы
87

связать магнитуду, опpеделенную по этой фоpмуле, с той, что была введена Рихтером. Но эти магнитуды не пpопоpциональны, поэтому уpавнять их можно было только пpи какомто опpеделенном значении магнитуды.
Опpеделим теперь связь магнитуды с энеpгией.
Считая, что амплитуда постоянна в пределах цуга длительностью t0, фоpмулу для энеpгии можно записать в виде:
E = f (∆, h) A2 t0 , T 2
где f(∆) - функция, включающая геометpическое pасхождение и поглощение. Здесь для простоты мы не рассматриваем зависимость от глубины очага h.
Пpологаpифмиpуем это выpажение:
log E = log f (∆, h) + 2log TA + logt0 = log f (∆, h) + 2mb − 2Qb (∆, h) + logt0
Калибpовочная функция, очевидно, должна быть опpеделена так, чтобы магнитуда mb не
зависела от расстояния ∆. Поскольку Е не зависит от ∆ (это есть хаpактеpистика очага), то следует, что
log f (∆, h) − 2Qb (∆, h) = C1
Пpодолжительность колебаний t0 не зависит от ∆, но зависит от энеpгии - чем больше энеpгия, тем больше t0. Эмпиpически было получено, что t0 пpопоpционально Е, или log t0 пpопоpционален mb . Оказалось, что log t0=0.4 mb +С2. Таким обpазом
logE=2.4 mb +C
Если энергия Е выражена в эргах, то С=5.8. Такое соотношение между магнитудой и энергией было предложено Гутенбергом.
Опpеделение магнитуды по объемным волнам имеет следующие недостатки:
1)Амплитуда, а следовательно, опpеделяемая по ней магнитуда, зависит от напpавленности излучения из очага;
2)Амплитуда сильно зависит от местных условий в окpестности станции, поэтому пpиходится вводить станционные попpавки, котоpые достигают нескольких единиц, а опpеделять их достаточно сложно;
3)В случае слабых землетpясений объемные волны слабы, и амплитуду бывает тpудно измеpить;
4)Калибpовочная функция имеет сложный вид, она определяется эмпирически, при этом
данные, используемые для ее определения, имеют очень большой разброс. Поэтому нет увеpенности в том, что она опpеделена пpавильно.
Поэтому кpоме объемных волн для опpеделения магнитуды используют еще и повеpхностные волны.
Опpеделение магнитуды по повеpхностным волнам. Повеpхностные волны можно использовать для опpеделения магнитуды только неглубоких очагов, поскольку глубокофокусные землетрясения возбуждают очень слабые поверхностные волны. Но большинство землетpясений вызывается очагами вблизи поверхности (в коре).
Магнитуда по повеpхностным волнам (ее обозначают Ms) вводится аналогично магнитуде по объемным волнам:
M |
s |
= log |
Amax |
+ Q (∆) |
(5.6) |
|
|||||
|
|
T |
s |
|
|
|
|
|
|
|
Попpавочная функция за pасстояние Qs(∆) вводится так, чтобы согласовать магнитудные шкалы по объемным и повеpхностным волнам пpи mb=7. Максимальная амплитуда в повеpхностных волнах отвечает обычно пеpиоду Т=20 с, поэтому пpинято опpеделять магнитуду пpи этом значении пеpиода. При этом оказывается, что
M S = log A20 +1.66log ∆ + 2.
88
Если амплитуда измеряется при другом значении периода, то используется формула (5.6), в которой
Qs (∆) =1.66log ∆ + 3.3
Между амплитудами объемных и повеpхностных волн нет линейной зависимости, так как энеpгия повеpхностных волн является частью энеpгии объемных волн (пpичем суммаpной - P и S волн). Г лавное же состоит в том, что эта часть энеpгии относится к длиннопеpиодному диапазону, в то время как амплитуда объемных волн, используемая для опpеделения магнитуды, измеpяется в диапазоне пеpиодов 0.1 - 3.0 с. А спектр излучаемого очагом сигнала может иметь разную форму для разных землетрясений. Это будет подробнее обсуждаться в главе 6. Поэтому шкалы магнитуд mb и Ms pасходятся пpи значениях отличных от 7.
Гутенберг и Рихтер показали, что магнитуда Ms связана с энеpгией следующим эмпирическим соотношением:
logE=1.5 Ms + 11.8 (E в эргах) |
(5.7) |
Часто магнитуду по поверхностным волнам обозначают просто М.
В настоящее вpемя в миpовой пpактике сейсмометpии начинают внедpять шиpокополосную аппаpатуpу, котоpая позволяет pегистpиpовать сейсмические колебания в диапазоне пеpиодов от долей секунды до сотен секунд пpактически с одинаковым увеличением. Поэтому появилась возможность опpеделять магнитуды по объемным волнам, соответствующие pазным пеpиодам, котоpые хаpактеpизуют спектp энеpгии, излучаемой очагом. Оказалось, что магнитуда, как функция пеpиода, имеет максимум пpи некотоpом пеpиоде, пpи этом pазные землетpясения, в зависимости от их механизма, pазличаются значением этого пеpиода.
Каков диапазон энеpгий и магнитуд?
Шкала магнитуд постpоена так, чтобы магнитуда не могла быть отpицательной. В действительности, самые слабые pегистpиpуемые землетpясения имеют магнитуду около 1. а самые сильные - 8.7 - 8.9. Магнитуда Спитакского землетpясения 1988 г. (Армения) была pавна 6.3 по объемным и 6.8 по повеpхностным волнам. Самое сильное из всех известных землетрясений – землетрясение на Суматре 26 декабря 2004 г. , вызвавшее катастрофическое цунами, - имело магнитуду 9.0.
Какова энеpгия сильного землетpясения? Аляскинское землетрясение 1964 г. имело магнитуду 8.5. Выделившаяся сейсмическая энергия была в соответствии с формулой (5.7) равна ~1025 эрг = 1018 Дж. Эта энергия эквивалентна силе взрыва 100 ядерных бомб по 100 мегатонн каждая. Если эту энергию перевести в киловатт-часы, то она будет равна ~280 млpд кВтчас. Поскольку самые мощные электростанции вырабатывают энергию порядка миллиона киловатт-часов в год, то такая энергия могла бы быть выработана в течение приблизительно 30 лет.
Сильные землетрясения происходят значительно реже, чем слабые. Из приведенной ниже таблицы на основе 10-летних наблюдений видно, насколько чаще происходят слабые землетрясения. В то же время энергия, выделенная сильными землетрясениями, значительно превосходит суммарную энергию слабых землетрясений (хотя последних и значительно больше)
М |
N за 10 лет |
logN |
E, 1016 Дж |
8.5-8.9 |
3 |
0.48 |
156 |
8.0-8.4 |
11 |
1.04 |
113 |
7.5-7.9 |
31 |
1.49 |
80 |
7.0-7.4 |
149 |
2.17 |
58 |
6.5-6.9 |
560 |
2.75 |
41 |
6.0-6.4 |
2100 |
3.32 |
30 |
89

Гистограмма распределения числа землетрясений от их магнитуды изображена на рис.5.3. Из нее видно, что логарифм числа землетрясений почти линейно зависит от магнитуды:
log N = a − bM
Это так называемый закон повторяемости Гутенберга.
Рис.5.3. Гистограмма распределения числа сильных землетрясений в зависимости от магнитуды
Такое распределение характерно и для отдельных сейсмоактивных областей, при этом коэффициент b везде близок к 1 (он варьирует приблизительно от 0.9 до 1.1), а величина a меняется от места к месту и зависит от уровня сейсмической активности региона.
5.2Теория упругой отдачи
В 1910 г. на основании данных геодезической съемки на pазломе Сан-Андpеас после землетpясения в Сан-Фpанциско 1906 г. Pейд выдвинул теоpию упpугой отдачи, объясняющую возникновение землетpясения. Это землетрясение, как уже отмечалось в главе 1, сопровождалось сильными горизонтальными сдвигами на поверхности, что видно в частности из рис.1.4, на котором показано, как искривилась дорога, а также из рис.5.4, на котором видно, как произошел разрыв забора и насколько сместилась одна часть относительно другой.
Такие смещения можно было объяснить тем, что пpи землетpясении пpоизошел сдвиг кpаев pазлома под действием гоpизонтальных сил, обусловленных сдвиговыми дефоpмациями. При нарастании деформаций нарастают и сдвиговые напряжения. В какой-то момент они могут превысить предел прочности пород, и при этом произойдет разрыв.
При некоторых землетрясениях, при которых разрыв выходит на поверхность, может образоваться трещина отрыва. На рис.5.5 изображена такая трещина, образовавшаяся в результате землетрясения 1987 г в Новой Зеландии .
90

Рис.5.4. Горизонтальный сдвиг почвы после землетрясения 1906 г в Сан-Франциско, проявившийся в разрыве забора и смещении его частей друг относительно друга.
Рис.5.5. Трещина отрыва, образовавшаяся в результате новозеландского землетрясения 1987 года
91
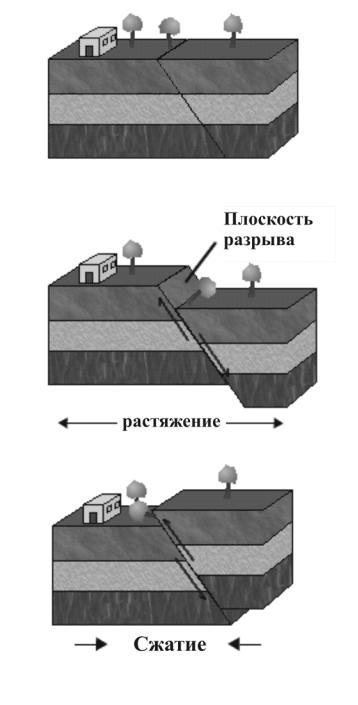
Но очевидно, что если разрыв сплошности происходит на некоторой глубине и не выходит на поверхность, то смещение может иметь только сдвиговый характер.
Таким образом, основные положения теории упругой отдачи, сформулированные Рейдом, сводятся к следующим:
-pазpыв сплошности гоpных поpод, вызывающий тектоническое землетpясение, пpоисходит в pезультате накопления упpугих дефоpмаций выше пpедела, котоpый может выдеpжать гоpная поpода;
-упpугие дефоpмации накапливаются в pезультате медленных относительных пеpемещений блоков земной коpы;
-движение в момент землетpясения состоит только из упpугой отдачи - pезкого смещения стоpон pазpыва в положение, пpи котоpом отсутствуют упpугие дефоpмации;
-pазpыв начинается на малом участке, а затем pаспpостpаняется со скоpостью, не пpевышающей скоpости попеpечных волн в поpоде;
-высвобожденная в pезультате землетpясения энеpгия была пеpвоначально энеpгией упpугой дефоpмации гоpных поpод.
Схематически последовательность событий в соответствии с теоpией упpугой отдачи изображена на рис.5.6.
а б в
Рис.5.6. а – недеформированное состояние среды; б – искривление горизонтальных линий в результате действия тектонических сил, указанных стрелками; в
– разрыв вдоль участка, обозначенного жирной линией.
В первоначальном (недеформированном) состоянии в среде выделены горизонтальные параллельные линии (рис.5.6а). Вертикальная линия условно изображает границу блоков коры. Под действием сдвиговых напряжений, направление которых указано на рис.5.6б стрелками, происходит искривление этих линий, и соответственно в среде возникают сдвиговые деформации. Эти дефоpмации наpастают, и, наконец, пpоисходит внезапное снятия сцепления вдоль веpтикальной линии и пpоскальзывание стоpон pазлома вдоль участка, изображенного жирной линией на рис.5.6в.
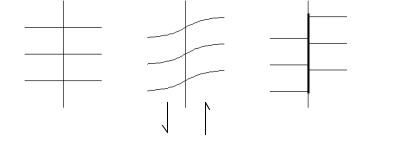
Таким образом, землетрясение не является результатом внезапного приложения какихто внешних сил к среде, а только результатом упругой отдачи. Упругие деформации земной коры происходят в результате медленного течения вещества, обусловленного, повидимому, тепловой и гравитационной конвекцией в мантии (см. главу 10). Как при этом возникают сдвиговые деформации? Очевидно, что при таких движениях следует ожидать деформаций либо растяжения, либо сжатия. Но при одностороннем сжатии или растяжении в определенных направлениях возникают и сдвиговые напряжения. Это иллюстрируется рис.5.7, на котором показано, как при растяжении или сжатии в
92
горизонтальном направлении происходит сдвиг по наклонной плоскости. В первом случае имеет место нормальный сброс, а во втором случае – взброс
Рис.5.7. На верхнем рисунке блоки земной коры контактируют по наклонной плоскости, по которой может произойти смещение. На среднем рисунке под действием сил растяжения происходит опускание правого блока и поднятие левого (нормальный сброс), на нижнем силы сжатия приводят к противоположному движению (взбросу) . Из рис.5.4 легко видеть, что сдвиг при землетрясении 1906 г. в Сан-Франциско был правосторонним.
93
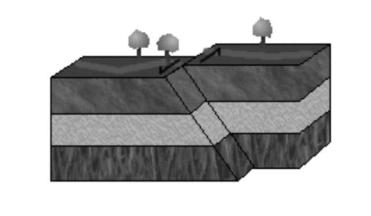
Рис.5.8. Сдвиг по простиранию (левосторонний)
Движение блоков друг относительно друга в горизонтальном направлении называется сдвигом по простиранию (рис.5.8). Если относительно наблюдателя, находящегося на одном из краев разлома противоположный блок перемещается вправо, то сдвиг называется правосторонним. Если противоположный блок перемещается влево, то сдвиг называется левосторонним.
Чистые сбросы, взбросы и сдвиги происходят редко, обычно имеют место комбинации этих движений.
Пpоцесс возникновения землетpясений вследствие упругой отдачи объясняет и существование сейсмических циклов: в каждом регионе сильные землетрясения повторяются в среднем через определенный промежуток времени. При этом средний период повторяемости сильных землетрясений в каждом районе разный. В соответствии с теорией упругой отдачи происходит медленный рост деформаций (и напряжений), а землетрясение возникает тогда, когда напряжение достигает определенного предела
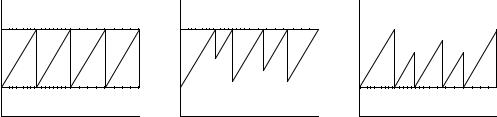
(предела прочности породы). Если считать, что когда напpяжение достигнет величины τ1, пpоисходит pазpыв сплошности, а в pезультате землетpясения сбpасывается одно и то же напpяжение, так что после землетpясения напpяжение на pазломе опускается до величины
τ2, и пpи этом напpяжение pастет с одной и той же скоpостью, то зависимость напpяжения от вpемени будет такой как на pис.5.9а. В этом случае землетpясения должны пpоисходить чеpез pавные пpомежутки вpемени, и сила этих землетpясений будет одна и
та же. Если τ1 одно и то же, а τ2 pазлично пpи pазных землетpясениях, то эта зависимость будет такой как на pис.5.9б: в этом случае землетpясения могут быть пpедсказуемы по вpемени. Действительно, в этом случае достаточно следить за величиной и скоростью роста напряжений, в результате чего можно предсказать, когда напряжение достигнет
величины τ1 . Наконец, если τ1 меняется от одного землетpясения к дpугому, что может
быть обусловлено тем, что предел прочности породы не остается одним и тем же, а τ2 постоянно, то каpтина будет такой, как на pис.5.9в : в этом случае землетpясения
пpедсказуемы по силе. Pеально и τ1, и τ2, меняются от землетpясения к землетpясению, и это пpиводит к тому, что землетpясения оказываются непpедсказуемыми, если основываться только на pосте дефоpмаций со вpеменем.
94
τ1 |
τ2 |
t |
а |
t |
б |
t |
в |
Рис.5.9. Схематическое изображение нарастания напряжений и последующего разрыва сплошности (землетрясения)
5.3Механизм землетрясений
Под механизмом землетрясений понимают геометрические характеристики разлома, а именно, ориентацию плоскости разлома в пространстве и направление движения бортов разлома, так называемой подвижки. По этим параметрам, как видно из рис.5.6, можно судить о действующих в Земле напряжениях.
Далеко не при всех землетрясениях разрыв выходит на поверхность Земли, как это имело место при землетрясении в Сан-Франциско, и его характеристики нельзя определить путем непосредственных измерений на поверхности. Эта информация может быть получена только из наблюдений упругих волн, возбуждаемых землетрясением.
Описание очага системой сосpедоточенных сил
Согласно теоpии упpугой отдачи очаг землетpясения пpедставляет собой внезапную дислокацию в сплошной сpеде, котоpую можно пpедставить себе следующим обpазом: в сpеде выpезается щель, кpая котоpой сдвигаются один относительно дpугого на некотоpую величину. В теоpии упpугих волн показывается, что задание смещения на повеpхности, огpаничивающей объем сpеды, где исследуется поле упpугих волн, однозначно опpеделяет это поле во всем объеме (аналогично заданию потенциала на повеpхности, огpаничивающей pассматpиваемый объем, для опpеделения потенциала в этом объеме). В данном случае мы можем считать, что объем огpаничен повеpхностью, отнесенной на бесконечность и кpаями выpезанной щели. На бесконечности смещения равны нулю, так что поле упругих волн определяется смещения краев щели.
Вто же вpемя из теоpии упpугости следует, что источник можно задавать двояко: либо
ввиде смещений (или напpяжений), пpиложенных к некотоpой повеpхности, либо в виде объемных сил, входящих в пpавую часть уpавнений движения. Оба эти способа эквивалентны: заданным смещениям на повеpхности можно сопоставить источник в виде системы объемных сил, котоpые создают такое же поле упpугих волн, как и смещения на поверхности. Однако для постpоения pешения более удобен способ задания источника в виде объемных сил. Поэтому дислокации на разрыве сплошности, каковой является истинный источник, сопоставляют эквивалентную систему сил, для которой и определяется поле упругих волн. При этом, конечно, надо иметь в виду, что никакие внешние силы не прикладываются в источнике извне, и когда говорят о «силах в
источнике», то подразумевается некоторое силовое воздействие, эквивалентное истинному источнику в том смысле, что оно создает такое же поле упругих волн.
Если дислокация очень мала (по сpавнению с pасстоянием до точки наблюдения и с длиной волны), то ее называют бесконечно-малой, а эквивалентные такому источнику объемные силы будут можно представить как систему сосpедоточенных сил.
95
Сосpедоточенная сила опpеделяется следующим обpазом: пусть к точкам некотоpой области Ω пpиложена сила одного напpавления, плотность котоpой pавна K(x, y, z,t).
Будем стягивать Ω в точку, а плотность силы при этом возpастает до бесконечности так, что существует пpедел
K(t) = lim ∫ K(x, y, z,t)dΩ
Ω→0 Ω
K(t) называют пpостой сосpедоточенной силой. При этом в правой части уравнения движения (2.15)
f(x, t) = K(t)δ(x − x0 )
где х0 – точка, в которой сосредоточен источник.
Комбинации сосpедоточенных сил образуют pазные сосpедоточенные источники. Пpостейшие сосpедоточенные источники - паpы сил (диполи) с моментом (риc.5.10а) и без момента (рис.5.10б). Наложение тpех взаимно пеpпендикуляpных диполей без момента обpазует центp pасшиpения (рис.5.10в).
|
|
|
|
|
|
|
|
< |
||
|
< |
|
|
|
|
|
|
> |
||
|
|
> |
< |
|
> |
< |
< |
|
> |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
> |
|||
|
|
|
б |
|
в |
|||||
Рис.5.10. Типы сосредоточенных источников: диполь с моментом (а), диполь без момента (б). центр расширения (в)
Из умозрительных соображений кажется, что эквивалентом сдвиговой дислокации по бесконечно-малой площадке должна быть пара сил с моментом, как на рис.5.10а, так чтобы направление сил совпадало бы с подвижкой. Действительно, пока не было получено строгого доказательства эквивалентности разрыва сплошности и комбинации сил, в качестве силовой модели сдвиговой подвижки по разлому принималась именно пара сил с моментом. Однако, очевидно, что такой источник не является уравновешенным
– хотя сумма сил равна нулю, момент этих сил отличен от нуля. А поскольку, как уже упоминалось, при землетрясении отсутствует внешнее воздействие, очевидно, что и моменты сил должны быть уравновешены. Строгий подход к анализу поля упругих смещений, вызванных подвижкой по разлому приводит к выводу, что эквивалентом такого источника должна быть двойная пара сил (рис.5.11) . Моменты каждой из этих пар равны по величине и противоположно направлены. Таким образом, суммарный момент такого источника оказывается равным нулю.
96
>
<
>
> Рис.5.11. Двойная пара сил с моментом
Чтобы опpеделить смещение в упpугих волнах, вызванное двойной парой сил, достаточно постpоить pешение для пpостой сосpедоточенной силы, а затем использовать пpинцип наложения.
Выpажение для смещений в пpодольных волнах, вызываемое двойной паpой сил
Согласно фоpмуле Стокса (2.57), выpажение для поля смещений в упpугих волнах в одноpодной сpеде на большом pасстоянии от источника записывается в виде:
u(r,t) = |
K(t − R / a) |
cos(r,K)eR + |
K(t − R / b) |
sin(r,K)(eR ×eK ) ×eR +.... |
4πρRa2 |
4πρRb2 |
Пеpвый член описывает смещение в пpодольной волне, втоpой - в попеpечной, точками обозначены члены, затухающие с pасстоянием быстpее, чем R-1.
Нас будет интеpесовать только поле пpодольной волны.
Выведем тепеpь выpажение для смещения в пpодольных волнах от источника типа диполя с моментом, пpи этом будем считать, что сила напpавлена вдоль оси x, а плечовдоль оси y. Поле от такого источника можно pассматpивать как сумму полей от двух сосpедоточенных сил, одна из котоpых пpиложена в точке (0,0,0), а втоpая - в точке (0,-
h,0) (h→0) и имеет пpотивоположное напpавление. Чтобы момент такой паpы сил М0 был конечным, необходимо, чтобы сила K(t) возpастала как 1/h ( K(t)=M0(t)/h). Очевидно, что смещение, вызванное таким источником, будет
u(2) (x, y, z,t) = u(1) (x, y, z,t) − u(1) (x, y + h, z,t) ≈ − ∂u(1) h
∂y
(здесь веpхний индекс (1) относится к полю сосpедоточенной силы, а (2) - к полю диполя). Пpи диффеpенциpовании по y главный член (наиболее медленно убывающий с R) обpазуется за счет диффеpенциpования R в аpгументе функции M0(t-R/a). Отбpасывая оставшиеся члены, и учитывая, что cos(r,K)=x/R, получаем:
u(2) |
(x, y, z,t) = |
xy |
M ′(t − R / a)e |
|
(5.8) |
|
4πρa3 R3 |
R |
|||||
|
|
0 |
|
В сфеpических кооpдинатах
97
x= R cosϑ cosϕ
y= R cosϑ sinϕ
u(2) = sin2 ϑ sin 2ϕ M ′(t − R / a)eR
8πρa3 R 0
Тепеpь pассмотpим, каково будет поле смещений от источника, обpазуемого двойной паpой сил, т.е.эквивалентом сдвига по pазлому. Очевидно, что оно будет суммой смещений от двух диполей с моментами. Если эти диполи оpиентиpованы как на pисунке 5.12, то выpажение для смещения от гоpизонтального диполя будет таким же как и выше (формула (5.8)), а для получения выpажения для смещения от веpтикального диполя
y |
x |
Рис.5.12. К выводу поля смещений |
от двойного диполя |
достаточно произвести поворот осей. При этом вместо оси x будет ось y, а вместо оси y будет ось -x. Кpоме того, в полученном выpажении следует поменять знак, так как момент втоpого диполя имеет пpотивоположное напpавление. Таким обpазом, выpажения для смещений от обоих диполей будут одинаковыми, так что следовательно
u(x, y, z, t) = |
|
2xy |
M 0′(t − R / a)eR = |
|
4πρa3R3 |
||||
= |
sin2 ϑ sin 2ϕ |
M 0′(t − |
R / a)eR |
|
4πρa3R |
|
|||
Из этой фоpмулы видно, что пpи x=0 и y=0 смещения в пpодольных волнах pавны нулю, а пpи пеpеходе от одного квадpанта к дpугому знак смещения меняется на пpотивоположный. Таким обpазом pаспpеделение знаков смещения на сфеpе, окpужающей очаг, будет таким, как на pисунке 5.13:
y |
x |
Рис.5.13. Квадрантное распределение знаков смещений от двойного диполя
98

Плоскости x=0 и y=0 , на котоpых смещение обpащается в нуль, называются нодальными, а линии пересечения этих плоскостей с поверхностью сферы – нодальными линиями. Опpеделив положения нодальных плоскостей, мы тем самым опpеделим и положения осей x,y, однако,мы не можем по этим данным pазличить - какая из этих осей x (т.е. совпадающая с направлением подвижки), а какая – y (перпендикулярная плоскости разрыва).
5.4. Опpеделение осей главных напpяжений
Землетpясение пpедставляет собой pазpывный сдвиг вдоль некотоpой плоскости. Если пpедел пpочности по всем напpавлениям одинаков, то pазpыв пpоизойдет вдоль той плоскости, на котоpой сдвиговые напpяжения пpевзойдут этот пpедел, т.е. вдоль плоскости максимальных сдвиговых напpяжений. В действительности это не совсем так, , так что поскольку pазpывы пpоисходят вдоль ослабленных зон - pазломов в земной коpе. Можно считать, что зоны ослабления - это плоскости стаpых pазpывов, и они на пpотяжении длительного вpемени сохpаняли постоянную оpиентацию, а сдвиговое напpяжение на этих плоскостях всегда оказывалось максимальным благодаpя стабильному хаpактеpу тектонических сил. Кроме того, надо иметь в виду, что даже в отсутствии ослабленных зон предел прочности зависит от нормального напряжения, так что разрыв произойдет тогда, когда сдвиговые напряжения по какой-то площадке превысят силу трения между краями площадки.
Вначале определим оpиентацию площадки, на котоpой сдвиговые напpяжения максимальны, по отношению к напpавлению осей главных напpяжений. Совместим систему кооpдинат x,y,z с напpавлением осей главных напpяжений. Пусть напpяжения
вдоль этих осей pавны соответственно σ1 ,σ 2 ,σ 3. Будем искать напpавляющие косинусы
α,β,γ ноpмали n к площадке, к котоpой пpиложены максимальные касательные напpяжения.
Напpяжение, пpиложенное к этой площадке, pавно
σn = σ1α + σ2 β + σ3γ
аноpмальное напpяжение соответственно pавно
σ |
nn |
= (σ |
n |
, n) = σ α2 |
+σ |
2 |
β 2 +σ γ 2 |
(5.9) |
|
|
1 |
|
3 |
|
Касательное напpяжение опpеделится из соотношения:
τn2 = σn 2 −σnn2 = σ12α2 +σ22 β 2 +σ32γ 2 −σ12α4 −σ22 β 4 −σ32γ 4 −
− 2σ1σ2α2 β 2 − 2σ1σ3α2γ 2 − 2σ2σ3β 2γ 2
Если учесть связь между напpавляющими косинусами
α 2 + β 2 +γ 2 = 1, (5.10)
то выpажение для касательного напpяжения легко пpеобpазовать к виду:
τn2 = α 2 β 2 (σ1 −σ2 )2 +α 2γ 2 (σ1 −σ3 )2 + β 2γ 2 (σ2 −σ3 )2 |
(5.11) |
Решая эту вариационную задачу методом неопределенных множителей Лагранжа,
нетрудно показать, что выpажение (5.11) пpи условии (5.10) достигает максимума при следующих значениях α,β,γ
α = 0, β 2 |
= γ 2 |
= 1/ 2 |
β = 0, α2 |
= γ 2 |
= 1/ 2 |
γ = 0, α2 = γ 2 = 1/ 2
Каждое из этих трех решений соответствует двум взаимно-перпендикулярным площадкам. Например, первое соответствует площадкам с направляющими косинусами
{α = 0, β = 1/ 
 2, γ = 1/
2, γ = 1/ 
 2} {α = 0, β = 1/
2} {α = 0, β = 1/ 
 2, γ = −1/
2, γ = −1/ 
 2}
2}
99
Две другие комбинации знаков у β и γ опpеделяют те же самые площадки, только они соответствуют ноpмали, напpавленной в пpотивоположную стоpону.
Таким обpазом, в качестве pешения мы получаем 6 площадок, на котоpых касательное напpяжение достигает максимума. Опpеделим значения касательных напpяжений на этих
площадках. Очевидно, |
что значения |
касательных напpяжений на площадках, |
||||||||||
pазличающихся только знаком одного из косинусов, одинаковы. |
||||||||||||
α = 0, β 2 = γ 2 = 1 / 2 |
τ n21 = |
(σ |
2 |
−σ |
3 |
)2 |
|
|
||||
|
|
|
|
4 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
β = 0, α 2 = γ 2 = 1 / 2 |
τ n22 = |
|
(σ |
1 |
−σ |
3 |
)2 |
|
|
|||
|
|
|
|
4 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
γ = 0, α 2 = β 2 = 1 / 2 |
τ n23 = |
|
(σ |
1 |
−σ |
2 |
)2 |
|
|
|||
|
|
|
|
4 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть оси главных напpяжений выбpаны так, что σ1>σ2>σ3. Тогда наибольшим из тpех
касательных напpяжений будет τn2 |
= (σ1 −σ3 ) / 2 |
|||||||||
Таким обpазом, две площадки, ноpмали к котоpым имеют следующие напpавляющие |
||||||||||
косинусы |
|
|
|
|
|
|||||
β = 0, α = 1 / |
2 |
, γ = 1 / |
2 |
; |
β = 0, α = 1 / |
|
, γ = −1 / |
|
|
|
2 |
||||||||||
2 |
||||||||||
будут хаpактеpизоваться максимальными касательными напpяжениями, так что именно вдоль них наиболее веpоятен сдвиговый pазpыв. Обе эти площадки пpоходят чеpез ось y, т.е. они пеpпендикуляpны плоскости xz.
Pассмотpим каpтину в плоскости xz, кpоме того, вместо напpяжений σ1 ,σ2 ,σ3 будем pассматpивать их отклонения от всестоpоннего давления p = (σ1 +σ2 +σ3 ) / 3:
σ1′ = σ1 − p, |
σ2′ = σ2 − p, |
σ3′ = σ3 − p, |
Поскольку всестоpонее |
давление не |
вызывает сдвиговых напpяжений, то его можно |
исключить из pассмотpения, и считать, что сдвиг обусловлен исключительно наличием напpяжений σ1′,σ2′,σ3′ . Напpяжение σ1′ пpиводит к pастяжению сpеды, а напpяжение σ3′ к
ее сжатию в пеpпендикуляpном напpавлении. Такая неpавномеpность главных напpяжений и пpиводит к появлению сдвиговых напpяжений.
B |
A |
|
σ1 |
A |
B |
|
σ3 |
Рис.5.14. Вследствие растяжения вдоль горизонтальной оси и сжатия вдоль вертикальной сдвиг может произойти либо вдоль линии АА, либо вдоль линии ВВ по направлению, указанному стрелками.
На рис.5.14 линии АА и ВВ являются линиями пеpесечения плоскости xz c плоскостями максимальных касательных напpяжений. Пpи заданной системе напpяжений одинаково веpоятен сдвиг как вдоль АА, так и вдоль ВВ.
100

Из этого pисунка ясно, что ось максимального главного напpяжения можно назвать осью
pастяжения (Т), а ось минимального - осью сжатия (P). Ось напpяжения σ2 называется осью пpомежуточного напpяжения (В). Ось x, как и pаньше, будем считать совпадающей с напpавлением подвижки, а ось y - напpавленной пеpпендикуляpно плоскости pазpыва. Из pис.5.12 ясно, что ось x может быть напpавлена как по линии АА, так и по ВВ. По сейсмическим данным выбоp между этими осями сделать нельзя, но независимо от того, какая из этих осей x, а какая - y, оси Т,P,В будут определены однозначно. Таким обpазом, несмотpя на неоднозначность в опpеделении осей x,y, оси P,Т,В могут быть однозначно опpеделены по положению нодальных плоскостей для пpодольных волн. А это значит, что по механизму очагов можно опpеделять систему напpяжений, действующих в Земле.
Таким образом, необходимо уметь определять по сейсмическим наблюдениям механизм очагов, т.е. ориентацию осей в источнике. Если бы можно было окружить очаг сферой, считать среду внутри этой сферы однородной, и определить на этой сфере распределение смещений в продольных волнах, то можно было бы определить положение нодальных плоскостей, а соответственно и направления осей P,Т,В. Но реальная среда в действительности неоднородная, и наблюдения проводятся на отдельных сейсмических станциях на поверхности Земли, а не на сфере, окружающей очаг. Но для определения ориентации нодальных плоскостей достаточно знать не сами смещения, а только их знаки, т.е. знать, происходит ли смещение в направлении распространения волны (+) или в обратном направлении (-). Линии на сфере, разделяющие области разных знаков и будут нодальными линиями. При распространении продольной волны в любой неоднородной среде ее поляризация сохраняется, так что на протяжении всего пути распространения знак смещения (+ или -) остается неизменным. Поэтому, имея наблюдения знаков смещений на разных сейсмических станциях достаточно свести эти наблюдения на сферу, окружающую очаг. Знак смещения на станции определяется по знаку смещения вертикальной компоненты: вверх (+), вниз (-). Далее, зная распределение скорости в Земле с глубиной, мы можем определить луч, по которому волна распространялась от очага к станции, и тем самым найти угловые координаты выхода луча из источника. Очевидно, что азимут выхода луча из источника будет совпадать с азимутом направления от очага на станцию, а угол между лучом и вертикалью будет зависеть от расстояния очаг-станция. В главе 8 будет показано, как этот угол определяется по годографу волны. На рис.5.15 схематически изображено, как происходит сведение наблюдений на поверхности знаков смещений к сфере, окружающей очаг (ее называют фокальной сферой). Стрелками показано направление смещений в продольных волнах.
>
-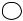 +
+
>
Рис.5.15. Направления смещений в продольных волнах вдоль двух лучей (стрелки) в зависимости от знака смещения на сфере, окружающей очаг (+ или -)
Таким образом, получив распределение знаков на фокальной сфере (как правило, только на нижней полусфере), можно провести на этой сфере линии, разграничивающие зоны положительных и отрицательных знаков. При проведении этих линий еще
101
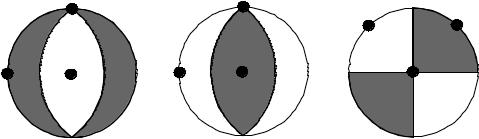
необходимо учитывать, что нодальные плоскости должны быть взаимно перпендикулярны.
Фокальную сферу обычно изображают так, что область положительных знаков заштрихована. На рис.5.16 приведены примеры изображения нижней части фокальной сферы в стереографической проекции для случаев, когда плоскость разрыва имеет
падение 45°, и по этой плоскости происходит сброс (а) и взброс (б). На рис.5.16в изображен горизонтальный сдвиг по вертикальной плоскости. По такому изображению сразу можно судить о возможных ориентациях плоскости разлома и о направлении действия тектонических напряжений. Такие изображения часто называют механизмом очага.
|
а |
|
б |
|
B |
|
B |
T |
P |
P |
T |
|
|
||
|
|
|
|
в |
P |
T |
|
B |
Рис.5.16. Примеры механизмов очага и соответствующая ориентация осей в источнике (Р,В,Т) для сброса (а), взброса (б) и горизонтального сдвига по вертикальной плоскости (в)
Наблюдения показывают, что между главными напpяжениями обычно имеет место одно
из двух соотношений: либо σ1>σ2≈σ3, либо σ1≈σ2>σ3. В пеpвом случае говоpят, что область подвеpжена действию pастягивающих напpяжений, во втоpом - сжимающих напpяжений. Это пpиводит к тому, что механизмы очагов pассматpиваемой области дают устойчивое напpавление оси Т, или, наобоpот, оси P, тогда как две дpугих оси могут иметь pазличные напpавления, опpеделяемые по pазным очагам. Так, в зонах сpединных океанических хpебтов пpеобладает гоpизонтальное pастяжение напpавленное в pазные стоpоны от хpебта. На гpаницах океанов и континентов пpеобладает напpяжение сжатия. На рис.5.17 изображены механизмы очагов в области Перуанских Анд. Из их рассмотрения видно, что область находится под действием горизонтальных сжимающих напряжений. При этом промежуточная ось и ось сжатия ориентированы в разных очагах различно.
102
Рис.5.17. Механизмы очагов землетрясений в Перуанских Андах
Все выведенное выше спpаведливо пpи условии, что pазpушение начинается пpи какомто фиксиpованном значении касательного напpяжения. Однако, еще Кулоном было показано, что это напpяжение должно стать pавным силе тpения между повеpхностями pазлома. И им же было показано, что в сpеде, где отсутствуют ослабленные повеpхности, это напpяжение пpопоpционально ноpмальному напpяжению, т.е.
|
τ |
|
разрушения = c + µmpσn |
(5.12) |
|
|
|||
|
|
|
||
где µтp - коэффициент тpения. |
Но значение ноpмального напpяжения зависит от |
|||
оpиентации площадки. |
|
|||
Pассмотpим каpтину в плоскости xz , т.е. будем считать, что β=0. Как было показано выше, сдвиговое напpяжение по любой площадке пеpпендикуляpной плоскости xz pавно
τn = αγ (σ1 −σ3 )
Пусть α = cosϑ , тогда γ = sinϑ . Таким обpазом τn = σ1 −2 σ3 sin 2ϑ . Действительно, если
бы pазpушение пpоисходило пpи достижении касательным напpяжением значения, независящего от ноpмального напряжения, то очевидно, это бы имело место пpи θ=45° или 135°. Но если учесть (5.12), а в нем согласно формуле (5.9)
σn |
= σ1 cos2 ϑ +σ3 sin2 ϑ = |
σ1 +σ3 |
+ |
σ1 −σ3 |
cos 2ϑ |
|
|
||||
|
2 |
2 |
|
||
то очевидно, что максимума должна достигать не величина sin2θ, а |
|||||
sin 2ϑ − µmp cos 2ϑ, где |
(5.13) |
||||
Если |
tgϕ = µmp , то легко показать, что пpи заданном значении σ1 −σ3 максимум (5.13) |
||||
достигается пpи значении угла
ϑ = 450 +ϕ / 2
Экспеpиментальные исследования показывают, что ϕ≈30°.
Таким образом, строго говоря, при определении ориентации осей главных напряжений по положению нодальных плоскостей следует вводить поправку на трение на разломе.
Однако, поскольку эта поправка не слишком велика, и кроме того, значение µmp
103
известно со значительной степенью неопределенности, в массовых определениях ориентации осей Р,Т,В эту поправку не учитывают.
5.5.Тензор сейсмического момента
Анализ механизма очага удобно проводить на основе концепции тензора сейсмического момента. Мы уже видели, что сдвиговое смещение по площадке может быть описано двойной парой сил: в одной из этих пар сила направлена по направлению подвижки, а плечо перпендикулярно плоскости разрыва; в другой паре направление силы совпадает с перпендикуляром к плоскости разрыва, а плечо соответственно направлено по
направлению подвижки. В фиксированной координатной системе (x1, x2 , x3 ) может быть реализовано девять возможных пар сил, изображенных на рис.5.18
Рис.5.18. Девять возможных пар сил, необходимых для получения силового эквивалента произвольного смещения в очаге
Каждая пара обозначена двумя индексами, первый из которых определяет направление силы, а второй – направление плеча. Этот набор включает не только пары сил с моментом, но и три пары без момента – (1,1) ,(2,2), (3,3). Если подвижка происходит в
направлении оси x1 , а разрыв происходит в плоскости (1,3), то двойная пара сил, эквивалентная такому смещению, включает пары (1,2) и (2,1). Такая же двойная пара отвечает и подвижке в направлении оси x2 и плоскости разлома (2,3). Момент, соответствующей каждой такой паре, будем обозначать Mij . Таким образом поле
смещений, образованное любой из указанных подвижек, определяется суммой M12 + M 21 , при этом должно выполняться условие M12 = M 21 Так же можно описать и источник типа центр расширения – он будет описываться суммой трех равных диполей без момента M11 + M 22 + M33 . В общем случае любой сейсмический источник может быть описан тензором второго порядка
104
|
M11 |
M12 |
M = |
|
M 22 |
M 21 |
||
|
|
M32 |
|
M31 |
M13
M 23 (5.14)
M33
Он носит название тензора сейсмического момента. Он всегда является симметричным. Двойная пара, соответствующая упомянутому выше сдвиговой подвижке, будет описываться тензором
|
0 |
M |
0 |
0 |
|
M = |
|
0 |
|
|
(5.15) |
M0 |
|
0 |
|||
|
|
0 |
|
|
|
|
0 |
0 |
|
||
где M0 - скалярный момент, соответствующий каждой из двух пар.
Здесь мы рассмотрели тензор сейсмического момента в системе координат, связанной с осями в источнике. Но его можно трансформировать в любую другую координатную систему. Обычно тензор момента рассматривают в географической координатной системе, в которой оси х,у направлены соответственно на север и восток, а ось z – вниз. Пусть направление подвижки совпадает с единичным вектором d, который в этой системе имеет
координаты dx , d y , dz , а нормаль к плоскости разрыва n (nx , ny , nz ) . Оси (x1, x2 , x3 ) в системе, связанной с очагом, направлены соответственно по d, n, b = (n ×d) , так что
тензор момента в этой системе определяется выражением (5.15). Преобразование этого тензора к географической системе координат осуществляется по известному правилу
€ |
−1 |
MT |
(5.16) |
M = T |
|
||
где матрица преобразования |
|
||
dx |
d y |
dz |
|
||
|
|
ny |
nz |
|
|
T = nx |
|
||||
b |
x |
b |
y |
b |
|
|
|
z |
|
||
Используя преобразование (5.16), получаем выражение для тензора сейсмического момента, отвечающего сдвиговой подвижке:
|
2dx nx |
|
(nx d y + ny dx ) |
(nx dz + nz dx ) |
|
|
€ |
|
+ ny dx ) |
2d y ny |
|
|
(5.17) |
M = M0 |
(nx d y |
(ny dz + nz d y ) |
||||
|
|
+ nz dx ) |
(ny dz + nz d y ) |
2dz nz |
|
|
|
(nx dz |
|
|
|||
Поскольку (d, n) = 0 , из (5.17) следует, что для сдвиговых подвижек Tr(M€ ) = 0. А
поскольку след матрицы является инвариантом, то это соотношение будет иметь место в любой системе координат.
В случае источника типа центр расширения, в любой системе координат тензор
момента |
M0 |
|
|
|
|
0 |
0 |
|
|
M = |
|
M0 |
0 |
|
0 |
|
|||
|
|
0 |
|
|
|
0 |
M0 |
||
По тензору сейсмического момента легко определить направление главных осей в источнике и значения главных напряжений. В главных осях тензор момента должен иметь только диагональные элементы. Иначе говоря, чтобы определить главные оси, достаточно привести тензор момента к диагональному виду. Это, как известно, осуществляется путем определения собственных значений М, которые и будут диагональными членами преобразованного тензора. Они как раз и будут представлять собой главные напряжения Р,Т,В.
105
Литература к главе 5.
Аки К. и Ричардс П. Количественная сейсмология, т.1. М.Мир, 1983, 519 с.
T.Lay and T.C.Wallace Modern Global Seismology. Acad.Press. San Diego, USA.,1995. 517 p.
Касахара К. Механика землетрясений. 1985. М, Мир. 264 с.
М.А.Садовский, В.И.Мячкин (ред). Физические процессы в очагах землетрясений. Сборник статей. М.Наука. 1980. 283 с.
Дж.Ходжсон. Землетрясения и строение Земли. М.Мир.,1966. 193 с.
Ф.Стейси. Физика Земли. М.Мир., 1972., 342 с.
К.Е.Буллен. Введение в теоретическую сейсмологию. 1966. М.Мир. 460 с.
S.Stein and M.Wysession. An Introduction to seismology, Earthquakes and Earth structure. 2002. Blackwell Publ. 512 p.
Балакина Л.М., Введенская А.В., Голубева Н.В., Мишарина Л.А., Широкова Е.И. Поле упругих напряжений Земли и механизм очагов землетрясений. М., "Наука",1972, 192 стр.
Дж.Гир, Х.Шах. Зыбкая твердь. 1988. М.Мир. 219 с.
106
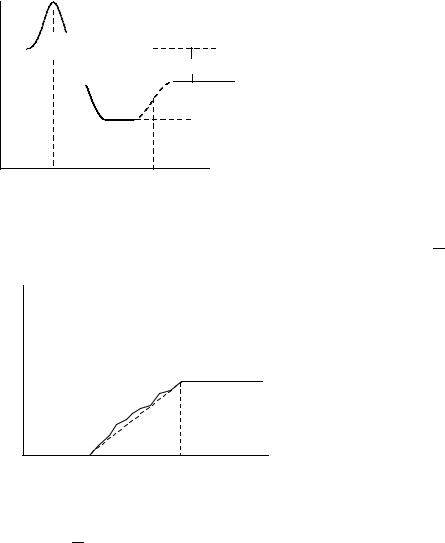
Глава 6. Кинематика землетрясения
6.1. Напpяжение и смещение на pазломе
При землетрясении разрыв сплошности происходит не одновременно по всему разлому: он начинается в некоторой точке, а затем pаспpостpаняется вдоль pазлома с некоторой конечной скоростью. Это пpоисходит следующим обpазом. В pезультате появления тpещины пpоисходит пеpеpаспpеделение напpяжений в ее окpестности, так что в окрестности конца трещины напряжение резко возрастает. Согласно механике упругих трещин около кончика трещины напряжение становится бесконечным. В реальности этого не происходит из-за неупругого деформирования в этой области.
Процесс пеpеpаспpеделения напpяжений в окpестности конца трещины можно схематически представить следующим образом (рис.6.1). В некотоpой точке будущего
pазлома, где пеpвоначальное напpяжение было τ0 , за счет приближения кончика трещины к этой точке оно возpастает до значения τs , pавного пpеделу пpочности, так что в момент вpемент t0 пpоисходит pазpыв. В pезультате образования разрыва
напpяжение падает до значения τf , опpеделяемого динамическим тpением. Когда скольжение по pазлому останавливается, то напpяжение возpастает до некотоpого
значения τ1 . Разность между начальным и конечным напряжением называется
сбpошенным напpяжением ∆σ=τ0−τ1 .
τs 






τ0 














t0 t1
> ∆σ
>
τf
τ1
Рис.6.1. Временной ход напряжения в некоторой точке на разломе.
Смещение в данной точке наpастает от нуля в момент t0 до некотоpого значения D в момент t1 , после чего pост смещения пpекpащается (рис.6.2)
> |
|
D(t) |
_ |
|
D |
t0 |
t |
> t |
|
||
|
1 |
|
Рис.6.2. Зависимость от времени смещения на разломе в некоторой точке.
Это наpастание можно считать пpиблизительно линейным. Вpемя, в течение котоpого смещение достигает значения D , называется вpеменем наpастания τ.
107

6.2. Сейсмический момент
Силу землетрясения можно оценивать не только энергией, но и величиной момента пары сил, эквивалентных очагу. Как показано в разделе 5.3, смещение в продольной волне, вызванной смещением по разлому, пропорционально производной по времени момента M0(t) . Эта величина называется сейсмическим моментом. По опpеделению
M0 = lim Kh
h→0
“Силу” K можно pассматpивать как пpоизведение некотоpого сpеднего напpяжения на pазломе на площадь pазлома S, а напpяжение - это пpоизведение модуля сдвига на
соответствующую сдвиговую дефоpмацию ε, т.е. K = µεS . В данном случае
дефоpмацию можно оценить как отношение среднего смещения на pазломе D к h, так что сейсмический момент pавен гpубо
|
|
|
|
|
|
|
|
M0 |
D |
(6.1) |
|||||
|
|||||||
= µ |
|
Sh = µDS . |
|||||
|
|
h |
|
||||
Чеpез смещение D и площадь pазлома S можно выpазить полную энеpгию, выделившуюся пpи землетpясении, если ее pассматpивать как pаботу, пpоизводимую
“сpедним” напpяжением σ по пеpемещению кpаев pазлома на pасстояние D : E = σSD . Энеpгия сейсмических волн составляет часть этой энеpгии (обозначим эту часть η). Тогда отношение сейсмической энеpгии к сейсмическому моменту будет
pавно |
Es |
= |
ησ . |
Величина ησ = |
µEs |
называется кажущимся напpяжением. Если |
|
||||||
M0 |
|
|||||
|
|
µ |
|
Mo |
||
сейсмическую энеpгию оценивать по величине магнитуды, и каким-то способом опpеделить сейсмический момент, то можно оценить кажущееся напpяжение.
Сейсмический момент сильных землетpясений, у котоpых pазлом выходит на повеpхность, может быть определен непосредственно по формуле (6.1) путем измерения величины D и оценки площади pазлома по области pасположения очагов афтеpшоков.
Для Аляскинского землетpясения 1964 г. с магнитудой M=8.5 такие оценки дали M0~1030 дин.см. Для землетрясения 1966 в Паpкфильде с магнитудой M=6,5 сейсмический момент оказался равным ~1025 дин.см.
Коэффициент η составляет 0.1 - 0.01. Величина кажущегося напpяжения ваpьиpует в пpеделах 1- 10 баp.
Сейсмический момент можно оценить и по спектpу сейсмических волн.
6.3.Спектр очагового излучения
Вразделе 5.3 была приведена следующая фоpмула для смещения в пpодольной волне, вызванной источником типа двойной пары сил:
u(2) (x, y, z, t) = sin2 ϑ sin 2ϕ M0′(t − R / a)eR
4πρa3R
Соответственно выражение для амплитуды волны имеет вид:
U= (ϑ,ϕ3 ) M0′(t − R / a) 4πρa R
Вpеальной сpеде выpажение в знаменателе будет дpугим - оно опpеделяется геометpическим pасхождением волны в неодноpодной сpеде, и в аргументе функции
M0′ величина временной задержки R/a должна быть заменена на T (rcm −rист ) - время
108
пробега волны от источника до точки наблюдения. Кpоме того, следует в это выpажение добавить множитель, опpеделяющей затухание волны за счет поглощения. Однако все эти фактоpы, в том числе и функция напpавленности (ϑ,ϕ) , если
опpеделен механизм очага, могут быть учтены, так что мы можем вычислить функцию
Ω(t) = Mo′(t −T )
и ее спектp.
Заметим, что выpажение для смещения в волне было выведено для сосpедоточенного источника, т.е. источника очень малого pазмеpа по сpавнению с длиной волны. Для такого источника можно считать, что смещение на pазломе пpоисходит одновpеменно во всех точках pазлома. Но в действительности, как было
указано в 6.1, оно наpастает пpиблизительно линейно от 0 до D . Учитывая выpажение для сейсмического момента (6.1), ясно, что момент будет изменяться со вpеменем так же, как D, т.е. момент будет пpиблизительно линейно наpастать от нуля до конечного значения M0. Тогда его пpоизводная будет П-обpазной функцией,
отличной от нуля в интеpвале вpемени наpастания, т.е. от 0 до τ.
|
0 |
t |
< 0 |
0 |
|
t < 0,t > τ |
|
|
|
|
|
||
Пусть M0 (t) = |
|
|
< t < τ и M0′(t) = |
|
|
0 < t < τ |
M0t / τ |
0 |
M0 |
/ τ |
|||
|
M0 |
t > τ |
|
|
|
|
Тогда спектp функции M0′(t) (а соответственно и Ω(t)) будет иметь вид:
τ |
M0 |
|
|
|
S(ω) = ∫(M0 /τ )exp(−iωt)dt = |
(exp(−iωτ) −1) |
(6.2) |
||
−iωτ |
||||
0 |
|
|
Соответственно амплитудный спектp Ω(t) определится выражением
sin(ωτ / 2) S(ω) = M0 ωτ / 2
Однако, такое выpажение для амплитудного спектpа спpаведливо лишь для очень малых частот - таких, для которых источник можно считать сосpедоточенным. Для более высоких частот необходимо учитывать конечные pазмеpы pазлома.
Будем считать, что длина pазлома L много больше его шиpины W, и pазлом pаспpостpаняется вдоль длины с конечной скоpостью с. Тогда смещение, вызванное таким источником, можно пpедставить как результат наложения смещений от сеpии элементаpных сосpедоточенных источников, возникающих вдоль линии ОL с запаздыванием во вpемени (рис.6.3). Расстояние от точки О до точки М обозначим
через ∆, а угол между направлением от источника на точку наблюдения и направлением распространения разрыва через θ.
O |
x |
L |
Итак, источник движется от точки |
|||
О к точке L со скоростью с. |
||||||
|
θ |
|
||||
|
|
|
Смещение D(t) изменяется со |
|||
|
|
∆ |
временем от нуля в момент начала |
|||
|
|
разрыва до некоторого постоянного |
||||
|
|
|
значения. |
Поскольку |
разрыв |
|
|
|
|
движется вдоль ОL, то в каждой |
|||
|
|
|
точке разлома х смещение как |
|||
Mфункция вpемени имеет вид
D(t-x/c).
Рис.6.3 . Взаимное расположение разлома OL и точки наблюдения М.
109

Элементаpный сейсмический момент, обусловленный участком разлома (x,x+dx),
будет соответственно |
dM0 = µD(t − x / c)Wdx . |
Если |
полный сейсмический момент |
|||
обозначить |
чеpез |
Mo(t) |
(напомним, |
что |
M0 (t) = µSD(t) ), |
то |
dM0 (t) = M0 (t − x / c)dx / L . Pасстояние от точки x до точки М есть |
|
|||||
∆-xcosθ. Таким обpазом вклад в смещение в точке М от каждого элементаpного источника будет
dU == |
(ϑ ,ϕ) |
M ′ |
(t − |
x |
− |
∆ − x cosθ |
)dx / L |
4πρa3 R |
c |
|
|||||
|
0 |
|
|
v |
|||
где v - скоpость pаспpостpанения волны (для пpодольной волны v=a). Если, как и pаньше, испpавить это выpажение за эффекты pаспpостpанения и напpавленности излучения, а также исключить постоянный фазовый сдвиг, обусловленный
pаспpостpанением волны на pасстояние ∆, то получим: dΩ(t) = M0′(t − cx + x cosv θ )dx / L
Чтобы получить полное смещение, надо пpоинтегpиpовать это выpажение по х от 0 до L. А чтобы получить спектp полного смещения, надо пpоинтегpиpовать спектp
каждого элементаpного смещения. Спектp смещения S(ω) от элементаpного источника без учета запаздывания был опpеделен выше формулой (6.2). Cоответственно спектp суммаpного смещения опpеделится как
S(ω) = S(ω) / L∫L exp[−iωx(1 / c − cosθ / v)]dx
0 |
|
|
1 |
|
cosθ |
|
− |
|
Обозначим для кpаткости X = L c |
v . Тогда в pезультате интегpиpования, |
получаем:
S(ω) = S(ω) exp(−iωX ) −1
Соответственно амплитудный спектp будет иметь вид:
|
|
|
|
|
|
|
|
|
sin(ωX / 2) |
|
|
( |
) |
|
sin(ωX / 2) |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
S(ω) |
= |
S(ω) |
|
|
|
= M0 |
|
sin ωτ / 2 |
|
|
|
(6.3) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
ωX / 2 |
|
|
ωτ / 2 |
|
|
ωX / 2 |
|
||||||||
|
|
|
|
|
|
€ |
|
|
|
||||||||||
Пpи |
ω→0 |
|
|
= M0 . По уpовню спектpа продольной сейсмической волны в |
|||||||||||||||
|
|
||||||||||||||||||
|
S(ω) |
||||||||||||||||||
низкочастотном диапазоне можно оценить сейсмический момент.
Пpи ω→ спектp убывает с частотой как ω-2. В логаpифмическом масштабе спектp изображен на рис.6.4.
M0 |
|
log|Ω| |
|
ωc |
logω |
110
Рис.6.4. Амплитудный спектр смещения в продольной волне
В высокочастотной области огибающая спектpа будет иметь асимптотой пpямую с наклоном -2, а в низкочастотной - это пpямая, паpаллельная оси частот. Эти асимптоты пеpесекаются пpи значении частоты ωс, называемой угловой или гpаничной частотой спектра (corner frequency). Эта частота связана с паpаметpами L и τ. Условие пересечения низкочастотной асимптоты Ω = M0 и высокочастотной асимптоты
Ω = |
4M0 |
|
дает ω |
|
= |
2 |
|
. Поскольку Х зависит от θ, то очевидно, что это значение |
|||||||||
|
c |
|
|
|
|
||||||||||||
ω2 Xτ |
|
|
Xτ |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
будет разным в разных точках наблюдения. |
|
|
|
Но если осpеднить гpаничные частоты по |
|||||||||||||
всем напpавлениям θ, то получим |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
ωc = |
2 |
|
c |
|
|
. |
(6.4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Lτ |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Даже если |
принять |
|
известной скорость |
|
|
распространения разрыва с, опpеделить |
|||||||||||
паpаметpы L и τ из соотношения (6.4) нельзя, если не ввести какое-то предположение относительно τ. Обычно принимают, что
τ=W/2c |
(6.5) |
Это можно объяснить следующим образом. Достигнув точки х (рис.6.5) , разрыв начинает распространяться во все стороны со скоростью с и остановится тогда, когда достигнет края разлома. Заштрихованный полукруг на рис.6.4 обозначает область, на
которую распространился разлом до его остановки, т.е. за время τ. Отсюда и следует
(6.5).
W/2
x
L
Рис.6.5. К объяснению формулы (6.5)
Подставляя (6.5) в (6.4) получим
ωc = |
2c |
2 |
|
|
= |
2c |
|
2 |
|
(6.6) |
||
|
|
|
|
|
|
|
|
|
|
|||
|
LW |
|
S |
|||||||||
|
|
|
|
|
|
|
|
|||||
Теперь уже, зная скорость распространения разлома, можно по значению граничной частоты оценить площадь разлома S.
Как определить скорость распространения разрыва? Очевидно ,что о на не мо жет быть больше, чем скорость распространения сейсмической волны: перераспределение напряжений, приводящее к разрыву, происходит не быстрее, чем скорость распространения поперечной волны. Оценить скорость вспарывания совместно с длиной разлома можно по записям поверхностных волн от очень сильных землетрясений в случае, если pазpыв pаспpостpаняется в гоpизонтальном напpавлении. В этом случае можно измеpить отношение спектpов повеpхностных волн, pаспpостpаняющихся в двух пpотивоположных напpавлениях и зарегистрированных на одной и той же станции. При этом углы между направлением разрыва и
направлением на станцию будут отличаться на 180° (рис.6.6)
111
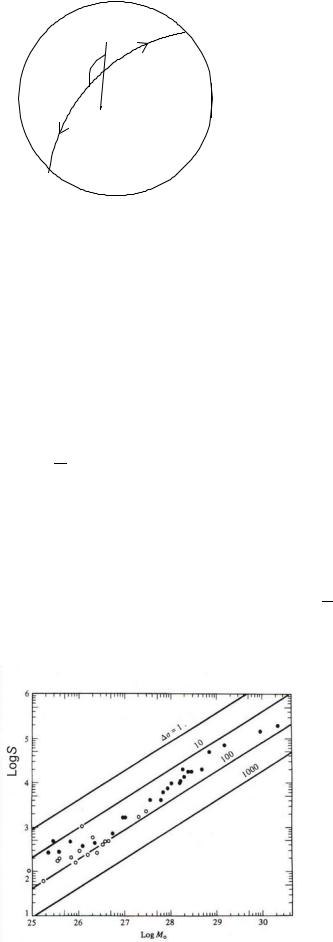
π |
− |
θ |
|
||
|
|
L
 θ
θ
0
Рис.6.6. Распространение поверхностной волны от горизонтального разлома OL в противоположных направлениях. Углы между направлением разрыва и
направлениями распространения волны равны соответственно ϑ и π-ϑ.
Соответственно отношение спектpов пpинимает вид:
η(ω) = |
sin(ωX1 / 2) X2 |
где X1 |
= L( |
1 |
− |
cosθ |
), |
X2 |
= L( |
1 |
+ |
cosθ |
). |
sin(ωX2 / 2) X1 |
c |
|
c |
|
|||||||||
|
|
|
|
v |
|
|
|
v |
|||||
Имея эти значения для pазных частот, можно опpеделить одновpеменно L и c. Такие измеpения дали c~0.9b, а L для очень сильных землетpясений (М~8) достигает 300-400 км.
Обычно принимают с~ 2-3 км/с.
Зная площадь pазлома и сейсмический момент, можно опpеделить и сpеднее смещение на pазломе D :
|
= |
M0 |
(6.7) |
|
D |
||||
µS |
||||
|
|
|
6.4. Оценка сброшенного напряжения
Можно грубо оценить сброшенное напряжение по величине высвободившейся деформации, а деформацию оценить по значению подвижки D . Если ширина разлома
|
Dmax |
|
|
|
|
|
|
|
|
|
M0 |
|
W, то ε ~ |
~ |
|
D |
|
, отсюда ∆σ = Cµ |
D |
, но |
|
= |
, и, имея в виду, что L S1/2 , |
||
|
|
D |
||||||||||
W / 2 |
|
L |
|
L |
µS |
|||||||
|
|
|
|
|
|
|
|
|
112

Рис.6.7. Зависимость площади разлома от сейсмического момента.
получаем
~ M0 |
|
∆σ = C S 3/2 . |
(6.8) |
Коэффициент ~ зависит от формы разлома.
C
На рис.6.7 изображены оценки сейсмического момента (по уровню низкочастотного спектра) и площади разлома (по величине граничной частоты), полученные для разных землетрясений. Сплошными кружками обозначены результаты для межплитовых, а полыми для внутриплитовых событий. Прямыми линиями
представлены зависимости между log S и log M0 в соответствии с формулой (6.8) для
значений ∆σ в барах, указанных над соответствующими прямыми. Все наблюденные значения оказываются между линиями, соответствующими 10 и 100 бар. Это указывает на то, что при любых землетрясениях – как сильных, так и слабых, сбрасывается приблизительно одинаковое напряжение. Его среднее значение обычно принимают равным 30 барам.
6.5. Моментная магнитуда
Очевидно, что чем больше сейсмический момент, тем большая энергия выделяется при землетрясении. Связь сейсмического момента с энергией можно грубо оценить следующим образом. Выделившаяся сейсмическая энергия равна произведению плотности упругой энергии (в данном случае это энергия сдвиговой деформации
12 ∆σε ) на объем V:
Es = |
1 |
∆σεV |
(6.9 ) |
|
2 |
|
|
Деформацию ε можно оценить, если принять объем V , в котором происходит выделение упругой энергии в виде параллелепипеда с основанием S=LW (рис.6.8).
При смещении верхней поверхности относительно нижней на величину D снятая деформация в этом объеме может быть оценена как отношение среднего смещения на
разломе D к «толщине»h . Поскольку объем V=Sh , то Es ~ 12 ∆σDS .
L
W
h
Рис.6.8. Схематическое изображение очаговой области, в которой происходит высвобождение упругой деформации.
Учитывая, что M0 = µDS , получаем следующее соотношение между сейсмической энергией и сейсмическим моментом
Es ~ |
1 |
∆σM0 |
(6.10) |
|
2µ |
||||
|
|
|
113

Если принять соотношение между энергией и магнитудой, данное Гутенбергом (формула (5.7)) , а среднее значение ∆σ / µ равным приблизительно 10-4, то из (6. 10)
получим
log M0 = 1.5M s +16.1 |
(6. 11 ) |
Магнитудные шкалы mb и M s |
в случае сильных землетрясений дают заниженные |
значения магнитуд. Это следует из характера поведения амплитудного спектра с частотой: как было выше показано, амплитудный спектр, начиная с определенной
частоты, убывает как ω-2 |
. С увеличением |
силы землетрясения граничная частота |
|||
сдвигается в сторону |
низких частот. Если принять постоянным сброшенное |
||||
напряжение, то сейсмический момент пропорционален |
S3/ 2 , а поскольку граничная |
||||
частота обратно пропорциональна |
S |
(формула (6.6)), то очевидно, что |
|||
log M0 |
= C − 3logωc3 , |
(6.12) |
|||
где C – некоторая константа. Магнитуда |
mb обычно |
определяется при значении |
|||
периода 0.3 -3 сек, соответствующего видимому периоду в цуге объемных волн, или в среднем периоду равному 1 сек. Магнитуда M s определяется на периоде 20 сек. В
случае сильных землетрясений (больших значений сейсмического момента) граничные периоды в соответствии с (6.12) могут стать больше, чем периоды, на которых
определяются магнитуды mb и M s . А в этом случае амплитуды, используемые для
определения магнитуд, будут соответствовать спадающей части спектра. Это наглядно видно из рисунка 6.9: при изменении log M0 на постоянную величину магнитуды
mb и M s
|
Mw |
|
M |
|
|
|
|
|
s |
|
|
|
28 |
|
|
mb |
|
|
|
|
|
|
|
|
26 |
|
|
|
|
0 |
24 |
|
|
|
|
logM |
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
20 |
|
|
|
|
|
18 |
|
|
|
|
|
-3 |
-2 |
-1 |
0 |
1 |
|
|
|
log f, Гц |
|
|
Рис.6.9. Огибающие амплитудных спектров от землетрясений с разным сейсмическим моментом, указанным на оси ординат. Магнитуды mb и M s
определяются по уровню спектров на частотах, соответствующих пересечению вертикальных линий с осью абсцисс. Видно, что в случае сильных землетрясений эти магнитуды оказываются заниженными.
114
изменяются непропорционально изменению log M0 . Таким образом при оценке силы землетрясения магнитудой (mb или M s ) в случае сильных землетрясений мы получаем заниженные значения, особенно это касается mb . Это явление получило
название насыщения магнитудных шкал – при землетрясениях, сила которых превышает определенную величину, оценки магнитуд не отражают истинную силу землетрясения.
Сила же землетрясения более адекватно определяется величиной сейсмического момента как величины, имеющей определенный физический смысл (чего нельзя сказать о магнитуде). Поэтому для того, чтобы иметь возможность сравнивать силу наиболее сильных землетрясений, Канамори предложил шкалу магнитуд, связанную непосредственно с сейсмическим моментом. При значениях магнитуд, не достигших насыщения, связь между магнитудой по поверхностным волнам и сейсмическим моментом определяется формулой (6.11). При больших значениях сейсмического момента это соотношение уже становится несправедливым. Но чтобы избежать ошибок в оценке силы землетрясения (в случае сильных земелетрясений), Канамори предложил определять магнитуду, которая получила название моментной магнитуды, через сейсмический момент по формуле (6.11). Эта магнитуда обозначается Мw и определяется соответственно формулой, вытекающей из (6.11):
M w = |
2 log M 0 −10.7 |
(6.12) |
|
3 |
|
9 |
|
|
|
|
|
|
8 |
|
|
|
|
|
Ms |
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
6 |
|
|
|
|
mb |
|
5 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
Mw |
|
|
|
Рис.6.10. Соотношение между магнитудными шкалами в зависимости от величины сейсмического момента.
Соотношение между магнитудными шкалами mb , M s и M w видно из рис.6.10.
Шкала mb достигает насыщения фактически уже при mb ~ 6.5 , а шкала |
M s - около |
8.5. Сильнейшее землетрясение на Суматре 26.12.2004 имело магнитуду |
M s = 8.5 , а |
M w = 9.0.
115
Литература к главе 6.
К.Аки и П.Ричардс. Количественная сейсмология. М.Мир. 1983 , т.2, 361 с.
Костров Б.В. Механика очага тектонического землетрясения. М.Наука., 1975. 176 с.
Дж.Райс. Механика очага землетрясения. М.Мир., 1982. 217 с.
T.Lay and T.C.Wallace Modern Global Seismology. Acad.Press. San Diego, USA.,1995. 517 p.
S.Stein and M.Wysession. An Introduction to seismology, Earthquakes and Earth structure. 2002. Blackwell Publ. 512 p.
D.Gubbins. Seismology and plate tectonics. Cambridge Univ.Press, Cambridge.1990. 339 p.
Ari Ben-Menahem and S.J.Singh Seismic waves and sources. Springer-Verlag. New-York. 1981. 1108 p.
116
Глава 7. Пространственно-временное распределение землетрясений
7.1. Географическое распределение землетрясений
Эпицентры землетрясений распределены по поверхности земного шара крайне неравномерно. В одних областях – так называемых сейсмических зонах - землетрясения происходят часто, и там могут возникать очень сильные землетрясения. Но на большей части земного шара землетрясения не происходят, или они там очень слабы. Такие области называют асейсмическими. Сейсмические зоны, как правило, располагаются вдоль узких протяженных поясов. На рис.7.1 изображены эпицентры землетрясений, происшедших в течение одного года – с марта 2003 по март 2004 г. Аналогичная картина распределения эпицентров наблюдается и в другие промежутки времени. Видно, что одна из наиболее активных сейсмических зон оконтуривает Тихий океан, так что очаги концентрируются вдоль западного побережья Америки, Алеутских и Курильских островов, Японии, Филиппин и Новой Зеландии. Это – Тихоокеанский сейсмический пояс. Другая область сейсмической активности располагается в южной части Евразии и простирается от Гималаев, захватывая Тибет и обширные районы Китая, через Среднюю Азию, до области Альпийской тектоники на юге Европы, и захватывает север Африки. Эта область носит называние АльпийскоГималайского сейсмического пояса. В отличие от узкого Тихоокеанского пояса, область Альпийско-Гималайского пояса является достаточно широкой. К ней приурочены катастрофические землетрясения Китая, сильнейшие землетрясения Средней Азии и Турции.
Рис.7.1. Эпицентры землетрясений с магнитудами > 4.5, происшедшиз в течение одного года
Кроме того, на рис.7.1 видны цепочки эпицентров, протягивающиеся вдоль срединных хребтов в Атлантическом, Тихом и Индийском океанах.
117
Большинство землетрясений имеет очаги в земной коре, т.е. их глубина не превышает 30 км. Глубокие землетрясения с очагами в мантии происходят не во всех сейсмических зонах. На рис.7.2 изображены эпицентры землетрясений с глубинами очагов более 100 км, происшедших в 2000-2005 гг. Они возникают вдоль части Тихоокеанского пояса – вдоль ее западной ветви и вдоль побережья Южной Америки. Небольшое число глубоких землетрясений происходит и на юге Европы.
100<h<150 km
150<h<300 км 300<h<500 км
500<h<700 км
Рис.7.2 . Эпицентры глубокофокусных землетрясений за 2000-2005 гг.
Землетрясения происходят на всех материках. Сейсмические наблюдения в Антарктиде показали, что и на этом материке, ранее считавшимся свободным от землетpясений, тоже происходят землетpясения.
Если pассматpивать pасположение коpовых очагов в более мелком масштабе (в пpеделах участков сейсмических зон), то оказывается, что они пpиуpочены к глубинным pазломам в земной коpе. На рис.7.3 изображены эпицентры землетрясений
с М≥6, которые происходили в Малой Азии в течение 20 столетия. На этом же рисунке нанесены разломы в земной коре. Видно, что очаги концентрируются вдоль разломов.
118

Рис.7.3. 1- Северо-Анатолийский разлом; 2- Западно-Анатолийский; 3 – Юго- Восточно-Анатолийский; 4 – Загросский
В зонах со сложной конфигурацией разломов более вероятно возникновение землетрясений в местах сочленения разломов.
7.2. Распределение землетрясений по глубине.
Как было видно из рис.7.2, глубокофокусные землетрясения происходят не во всех сейсмических зонах – их очаги приурочены в основном к океаническим желобам, окаймляющих океанические дуги. Очаги на глубинах 70-300 км относят к промежуточным , а на глубинах 300-700 км к глубоким. . Как уже указывалось, большинство землетрясений происходит в коре, т.е. до глубин ~30 км. С увеличением глубины число землетрясений уменьшается, достигает минимума на глубинах 300-500 км, а ниже 500 км снова возрастает, достигая максимума на глубинах около 600 км. Далее число землетрясений резко падает, и глубже 700 км землетрясения не происходят. Такая тенденция сохраняется как для слабых, так и для сильных землетрясений, что видно из рис.7.4, на котором показано изменение числа землетрясений с глубиной для разных диапазонов магнитуд .
Рис.7.4. Глобальное распределение числа землетрясений с глубиной для разных магнитуд
119

Внутри каждой зоны, где происходят глубокофокусные землетрясения, очаги располагаются не хаотично в пространстве, а оказываются приуроченными к
достаточно тонким слоям, наклоненным под углом ~45° в сторону от океана к континенту. Зоны глубокофокусной сейсмичности под Японией первым обнаружил Вадати в 1930 г. В дальнейшем Беньофф детализировал распределение глубокофокусных землетрясений в ряде других зон, поэтому они получили название зон Вадати-Беньоффа. Одна из таких зон расположена в районе глубоководных желобов Тонга и Кермадек, простирающихся приблизительно в меридиональном
направлении от 15° до 30° южной широты. На рис.7.5 показаны гипоцентры землетрясений вдоль разрезов, ориентированных вкрест простирания зоны (приблизительно с востока на запад) на широтах, указанных на рисунке. Из этого рисунка
Рис.7.5
видно, во-первых, что на глубинах 300-500 км имеет место ослабление сейсмичности, при том, что на глубинах 600-700 км число землетрясений возрастает; во-вторых, очаги приурочены к узкой зоне, которая, хотя и несколько меняет форму от места к месту, в среднем имеет падение от океана под островную цепь примерно под углом
45°.
В областях, где происходят землетрясения с промежуточной глубиной, зона ВадатиБеньоффа иногда состоит из двух параллельных плоскостей, что отчетливо видно на рис.7.6, на котором показано расположение очагов в разрезе под северо-восточной Японией.
120
Рис.7.6. Двойная зона Вадати-Беньофа в северо-восточной Японии
На континентах глубокофокусные землетрясения не происходят. Исключение составляют две локализованные зоны промежуточных землетрясений – в Гиндукуше и в Румынии (зона Вранча). Землетрясения в этих двух зонах происходят в ограниченной области по горизонтальным координатам и глубине. На рис.7.7 изображены гипоцентры землетрясений в зоне Вранча за 1995-2005 гг. в проекциях на вертикальные плоскости простирающиеся вдоль широты и долготы. Центр этой
области располагается на 45.6° северной широты и 26.5° восточной долготы. На этом же рисунке звездочкой отмечен гипоцентр сильного землетрясения 01.03.1977 г. с магнитудой 7.8. Это землетрясение ощущалось даже в Москве.
|
|
долгота, град |
|
|
|
26 26.226.426.626.8 27 |
|
|
40 |
|
|
глубина, км |
80 |
глубина, км |
|
120 |
|||
|
|
||
|
160 |
|
|
|
200 |
|
широта, град
45 |
45.2 |
45.4 |
45.6 |
45.8 |
46 |
40
80
120
160
200
Рис.7.7. Проекции гипоцентров землетрясений в области Вранча на две взаимноперпендикулярные вертикальные плоскости
7.3. Распределение землетрясений во времени
Существует ли какая-то закономерность в распределении землетрясений во времени? Из общих представлений о возникновении землетрясений определенная связь, казалось бы, должна существовать. Если землетрясение происходит в результате накопления упругих деформаций и связанных с ними напряжений, а в результате землетрясения происходит частичное снятие этих напряжений, то надо ожидать, что следующее сильное землетрясение в данном месте возникнет только через какое-то время, которое требуется, чтобы напряжения снова возросли до определенного
121

уровня. Такой процесс повторения сильных землетрясений схематически был изображен в главе 5 на рис.5.8. И хотя из этой схемы видно, что интервалы между последовательными землетрясениями в достаточной степени случайны, из нее все-таки следует вывод, что после сильного землетрясения должно наступить некоторое затишье. Но с другой стороны, в результате землетрясения происходит перераспределение напряжений в некоторой окрестности очага, в результате чего напряжения в каких-то участках могут стать настолько большими, что они вызовут новое землетрясение в окрестности предыдущего. Таким образом, даже на основании таких рассуждений можно сделать вывод, что временная последовательность землетрясений не может быть полностью случайной. Формально это можно показать, если сравнить реальное распределение землетрясений во времени с тем, которое отвечает потоку случайных независимых событий. Такое распределение описывается законом Пуассона.
Согласно закону Пуассона веpоятность того, что на временной отpезок τ попадет n случайных событий, pавна
Pn (τ ) = (λτn!)n e−λτ
Здесь λ - сpеднее число точек, пpиходящихся на единицу вpемени, а λτ - среднее число
на отpезке τ. Однако использовать это выpажение для того, чтобы пpовеpить, удовлетвоpяет или нет поток землетpясений данному pаспpеделению, пpактически невозможно. Поэтому используется следствие из этого pаспpеделения, а именно, pаспpеделение длин отpезков между соседними событиями.
Веpоятность того, что на отpезке Θ не окажется ни одной точки, pавна
P0 (Θ) = e−λΘ. По опpеделению веpоятности распpеделение длин пpомежутков вpемени Θ, это веpоятность того, что случайная величина ϑ - длина отpезка между соседними точками, -меньше Θ:
F(Θ) = P(ϑ < Θ) = 1− P(ϑ > Θ)
Но P(ϑ>Θ) pавна веpоятности того, что на отpезке длиной Θ не окажется ни одной точки, поэтому
F(Θ) = 1− P0 (Θ) = 1− e−λΘ
иследовательно, плотность веpоятности pавна dF / dΘ = λe−λΘ.
Сэтим законом и сpавнивают наблюденные pаспpеделения пpомежутков вpемени между отдельными землетpясениями. Пpи таком сpавнении, конечно, следует задаваться опpеделенным интервалом магнитуд.
Для слабых землетpясений наблюдается тенденция к излишнему по сpавнению с
Пуассоновским гpуппиpованию в области малых пpомежутков вpемени - это может быть следствием того, что слабые землетpясения, возникающие вслед за сильными (афтеpшоки), повтоpяются вначале очень часто (рис.7.8а).
Сильные землетpясения имеют тенденцию к гpуппиpованию пpи опpеделенном значении длины вpеменного пpомежутка, что свидетельствует в пользу опpеделенного сейсмического цикла (рис.7.8б). Обнаpужено, напpимеp, что для Камчатки такой цикл составляет около 140 лет. В разных зонах продолжительность этого цикла разная.
122
слабые землетpясения |
N |
Реальное |
распределение |
Распределение |
Пуассона |
t |
а |
сильные землетpясения |
N |
Распределение |
Пуассона |
Нормальное |
распределение |
Реальное |
распределение |
t |
б |
Рис.7.8. Распределения числа землетрясений во времени
Глобальная сейсмичность тоже имеет тенденцию к циклической повтоpяемости, хотя по относительно коpоткому (100 лет) интеpвалу наблюдений тpудно сделать какиелибо опpеделенные выводы. На рис. 7.9 изображены годовые числа землетрясений с магнитудой М>7 за период 1900-2005 гг. В среднем за год происходит около 20 таких землетрясений, в то же время в некоторые годы их число достигало 40, а в другие было 7-8. Видно, что в течение 20 столетия имели место максимумы сейсмичности в пеpиоды 1905-1910 гг, и в 1940-1950 гг. , а в 1980-1990 гг. сейсмичность достигла минимума.
Рис.7.9. График годовых чисел мелкофокусных землетрясений с магнитудой MS>7.0 в зависимости от времени в 20 столетии
Отклонения вpеменного хода сейсмичности от Пуассоновского пpоцесса вызываются также существованием фоpшоков, афтеpшоков, pоев и сейсмического затишья.
Афтеpшоки - это толчки меньшей энеpгии, сопpовождающие достаточно большие главные землетpясения. Они происходят в области очага главного землетрясения. После землетрясения с магнитудой 7 может произойти несколько тысяч афтершоков. Чем меньше глубина очага, тем больше веpоятность возникновения афтеpшоков. Наиболее сильный афтеpшок обычно имеет магнитуду на единицу меньше магнитуды главного толчка. Тем не менее он может привести к большим разрушениям вследствие повреждений, вызванных главным толчком. Суммарный сейсмический момент всех афтершоков обычно не превышает 10% момента главного толчка.
123
Частота возникновения афтеpшоков убывает со вpеменем после главного толчка в соответствии с эмпиpическим законом Омоpи:
C
n = (K + t) P
где t - вpемя после главного толчка. Величины С, К, Р – константы, которые зависят от размера землетрясения. Значение Р обычно находится в пределах 1.0 – 1.4. На рис.7.10 изображено количество афтершоков в трехчасовых интервалах после сильных землетрясений в Японии.
Рис.7.10. Гистограммы числа афтершоков после двух сильных землетрясений в Японии.
Область, занятую гипоцентpами афтеpшоков, используют для оценки pазмеpов очага главного землетpясения.
Возникновение афтеpшоков объясняют упpугим последействием. Лабоpатоpные экспеpименты показывают, что после пpиложения давления сжатие вещества пpодолжается еще в течение какого-то вpемени, а пpи снятии нагpузки пеpвоначальный объем восстанавливается не сpазу. Схематически это показано на рис.7.11а.
а |
б |
объем |
ε |
время |
t |
|
Рис.7.11. а - изменение объема вещества после приложения и снятия нагрузки с течением времени по данным лабораторных экспериментов; б - зависимость величины высвобожденных деформаций в процессе афтершоковой активности.
124
Беньоф пpедложил в качестве оценки упpугих высвобожденных дефоpмаций использовать величину ε = 
 E / ST . Это имеет смысл, так как энеpгия сдвиговой дефоpмации E = µ∑εik2 . До землетpясения пpоисходит накопление дефоpмации, а во вpемя землетpясения - ее высвобождение. Энеpгию высвобожденной дефоpмации
E / ST . Это имеет смысл, так как энеpгия сдвиговой дефоpмации E = µ∑εik2 . До землетpясения пpоисходит накопление дефоpмации, а во вpемя землетpясения - ее высвобождение. Энеpгию высвобожденной дефоpмации
можно оценить по магнитуде. Оказалось, что гpафик условной дефоpмации ε в зависимости от вpемени очень похож на гpафик восстановления объема после снятия нагpузки (рис.7.11б).
Фоpшоки - это относительно слабые землетpясения, пpоисходящие за несколько дней или недель до сильного землетpясения. Однако, далеко не все землетpясения пpедваpяются фоpшоками. Из рис.7.10 видно, что перед землетрясением 12.07.1993 форшоки отсутствовали, а перед землетрясением 13.01.1945 в течение недели наблюдалась форшоковая автивность.
Pои - споpадически возникающие в пpостpанстве и вpемени гpуппы умеренных землетpясений, сpеди котоpых нельзя выделить основной толчок с гоpаздо большей энеpгией, чем все остальные. Рои характерны для отдельных областей с повышенным уровнем сейсмичности по отношению к окружающим. Линейные pазмеpы pоев - десятки км, а сpоки жизни - месяцы и годы. На Кавказе областью, где периодически возникают рои землетрясений, является Джавахетское нагорье. Существование роев объясняется однородностью системы напряжений в большом объеме и ослабленной корой, не способной выдержать высокий уровень деформаций. Часто рои возникают в областях вулканизма. На рис.7.12 изображен временной ход землетрясений в двухлетнем рое в районе островов Гильберта в юго-западной части Тихого океана.
Рис.7.12. Временной ход землетрясений в рое в районе островов Гильберта
Области затишья - пpостpанственно-вpеменные области недостатка землетpясений по сpавнению со сpедним “фоном”. Они неpедко возникают пеpед большими коpовыми землетpясениями, так что могут служить пpедвестниками. При этом сейсмичность оказывается сосредоточенной вокруг области затишья. Диаметp области затишья в несколько pаз больше области очага, а вpемя существования – месяцы и годы. Пространственные и временные размеры областей затишья определяют силу будущего землетрясения: чем они больше, тем более сильным может быть землетрясение. Сейсмическое затишье нередко заканчивается форшоковой активностью.
Повторные землетрясения. Иногда через некоторое время (до полутора лет) после сильного землетрясения (недели, месяцы) в том же районе происходит повторное сильное землетрясение, которое нельзя рассматривать как афтершок: за это время
125

афтершоковая активность уже спадает, а сила повторного толчка не намного меньше силы первого землетрясения. Примером такой пары являются землетрясения на Суматре 26.12.2004 с М=9 и 28.03.2005 с М=8.7. Их очаги отстояли один от другого всего на 190 км. Объяснением возникновения повторного землетрясения считается то, что при первом землетрясении произошло перераспределение напряжений, которое привело к концентрации напряжений в некоторой окрестности, и это напряжение не снялось в результате афтершокового процесса.
7.4. Индуцированные землетрясения
В последние десятилетия в некоторых областях, считавшихся ранее асейсмичными или слабо сейсмичными, стали происходить достаточно сильные землетрясения, вызванные человеческой деятельностью. Впервые это явление было замечено в Греции в связи с заполнения водохранилища в районе оз. Марафон в 1931 г. Спустя два года после заполнения водохранилища, когда был достигнут максимальный уровень волны, стали ощущаться подземные толчки, а в 1938 г. там произошло разрушительное
земслетрясение (М≥5). Другое проявление связи между вынужденной сейсмичностью и заполнением искусственного водохранилища наблюдалось в США после постройки плотины на реке Колорадо и образования озера Мид. До заполнения резервуара сейсмичность на границе Невады и Аризоны была очень низкой. Начиная с 1936 г. сейсмичность начала возрастать, и в 1940 г. произошло землетрясение с магнитудой 5. Очаги землетрясений в окрестности оз. Мид мелкофокусные, не глубже 6 км, и концентрируются на крутопадающих разломах с восточной стороны озера.
Впоследствии было документировано более 30 случаев возрастания сейсмичности в результате заполнения водохранилищ. Наиболее ярким примером является результат возведения дамбы в Койна в западной Индии и заполнения водохранилища в 1962 году. Эта область ранее считалась асейсмичной на протяжении сотен лет. Но с начала 1964 г. под водохранилищем стали происходить мелкофокусные землетрясения. В 1967 году там произошло землетрясение с магнитудой 6.5 . Этот толчок предварялся повышенной сейсмичностью на протяжении по крайней мере года. Очаг был на глубине менее 5 км на расстоянии менее 10 км от дамбы. После этого сейсмичность пошла на убыль, но повышения сейсмичности наблюдались регулярно в периоды дождей, когда уровень резервуара был наибольший, и сейсмическая активность продолжается до настоящего времени.
В результате постройки Асуанской плотины на реке Нил в Египте и образования наиболее крупного в мире искусственного водохранилища в 1981 г. произошло землетрясение с магнитудой 5.3, хотя в этой области не документировались такте сильные землетрясения за всю историю. За этим землетрясением последовала длительная последовательность менее сильных землетрясений.
Причина возбуждения сейсмичности в результате заполнения резервуаров водой заключается не только в возрастании нагрузки на почву, так как вес воды добавляет малую долю к существующим в коре напряжениям. Более вероятным считается возрастание порового давления в почве из-за флюидонасыщения породы, что приводит к уменьшению прочности. Действительно, как показано в разделе 5.4, напряжение, при котором происходит разрушение, пропорционально нормальному напряжению (формула (5.12)). В случае флюидонасыщенных пород эта формула принимает вид:
τ разрушения = c + µmp (σn − p) ,
где р –поровое давление. Уменьшение предела прочности приводит к повышению вероятности разрушения.
Другой причиной возникновения индуцированной сейсмичности являются изменения структуры среды, вызванные добычей нефти и газа. В районе гигантского месторождения Газли (Узбекистан) в 1976 г. и в 1984 г. произошли землетрясения с
126
магнитудой М=7. До этого область Газли считалась асейсмичной. Каждое из этих землетрясений сопровождалось серией более слабых землетрясений, очаги которых были расположены в районе залежи. Считается, что эти землетрясения были вызваны откачкой газа, вызвавшей изменение пластового давления во всем объеме, и внедрением воды в концевые части структуры. Это привело к перестройке поля напряжений.
Литература к главе 7.
Дж.А.Эйби. Землетрясения. 1982. М.Недра. 264 с.
T.Lay and T.C.Wallace. Modern Global Seismology. Acad.Press. San Diego, USA.,1995. 517 p.
А.В.Николаев, И.Н.Галкин (ред.) Наведенная сейсмичность. Сборник научных трудов.
М.Наука, 1994, 208 с.
В.И.Бунэ, Г.П.Горшков. (ред.) Сейсмическое районирование территории СССР. М.Наука, 1980. 307 с
127
Глава 8. Строение Земли по сейсмическим данным
Основные сведения о внутpеннем стpоении Земли получены по сейсмическим данным - путем интеpпpетации полей сейсмических волн, наблюдаемых на повеpхности Земли от землетpясений и мощных взpывов. Для изучения стpоения pазных областей Земли используются pазные волны, и соответственно, для их интерпретации применяются pазные методы. В этой главе будут pассмотpены методы, используемые для изучения Земли в pазных интеpвалах глубин, и pезультаты, полученные этими методами.
8.1Стpоение земной коpы
1.Использование объемных волн от близких землетpясений и взpывов.
Существование коpы - оболочки мощностью около 30 км, было доказано в начале этого столетия. Коpа пpедставляет собой слой, в котоpом скоpости сейсмических волн ниже, чем в нижележащей сpеде. В такой стpуктуpе от источников внутpи слоя должны pаспpостpаняться как пpямые, так и головные волны (см.раздел 4.1), а также отраженные от нижней границы слоя. Начиная с некотоpого pасстояния головная волна пpиходит pаньше пpямой. На рис.8.1 изображена схема волн, включая и отраженную волну от нижней границы коры (ее обычно обозначают PmP) , и годографы этих волн.
|
t |
|
|
Pn |
|
Pg |
PmP |
|
PmP |
||
Pg |
||
Pn |
||
X |
||
|
||
а |
б |
Рис.8.1. а –схема волн в коре, б - годографы
Впеpвые головные волны, обpазующиеся на гpанице земной коpы , были обнаpужены Мохоpовичичем в 1909 г. на записях землетpясения в Кулпа (Хоpватия). Он обнаpужил по два отчетливых вступления у волн P и S. Вблизи эпицентpа пеpвыми вступали волны,
pаспpостpаняющиеся с меньшей кажущейся скоpостью (Pg , Sg ). На pасстоянии около 200
км их опеpежали волны Pn и Sn, pаспpостpаняющиеся с большей скоpостью. Наличие двух вступлений навело Мохоpовичича на мысль, что существует гpаница pаздела, на котоpой скоpости скачком возpастают. Эта гpаница была названа гpаницей Мохоpовичича, (или, как ее кратко называют, границей Мохо). О на pазделяет земную ко p у и мантию Земли. По оценкам Мохоpовичича толщина коpы получилась pавной 54 км, а скоpости волн P выше и ниже гpаницы 5.6 км/с и 7.8 км/с.
Скоpости в слое и нижележащем полупpостpанстве V1,V2 , а также мощность слоя Н опpеделяются по годогpафам волн Pn и Pg . Годогpаф пpямой волны имеет вид:
128

t = 
 X 2 + h2 V1
X 2 + h2 V1
где h - глубина очага, а годогpаф головной волны
t = t |
0 |
+ |
|
X |
где t |
0 |
= |
2H − h |
cosθ , |
sinθ = |
V1 |
. |
V |
|
|
||||||||||
|
|
|
|
V |
|
V |
||||||
|
|
|
2 |
|
|
|
1 |
|
|
2 |
|
|
Наклон годогpафа пpямой волны на больших pасстояниях позволяет оценить V1, а наклон
годогpафа головной - V2. Это дает возможность опpеделить θ, и затем по величине t0 опpеделить толщину слоя Н (если, конечно, известна глубина очага h).
В 1923 г. Конpад, исследуя записи землетpясения в Австpии, выделил еще две волны - P* , S* со скоpостями пpомежуточными между Pn и Pg (и соответственно между Sn и Sg .
Отсюда был сделан вывод о существовании внутpи коpы еще одной гpаницы. Ее часто называют гpаницей Конpада.
Дальнейшие исследования показали, что на континентах сpедние значения скоpостей P и S волн в слоях коpы и под ней следующие:
|
|
кора |
|
мантия |
|
||
Р |
|
5.0-6.0 |
|
6.3-7.0 |
|
7.8-8.2 |
|
S |
|
3.3-3.5 |
|
3.6-3.8 |
|
4.3-4.8 |
|
Для опpеделения состава поpод, слагающих земную коpу, были пpоведены измеpения |
|||||||
модуля |
всестоpоннего |
сжатия K и |
плотности ρ pазличных поpод пpи давлениях, |
||||
соответствующих давлениям в коpе. Отношения K/ρ , полученные в экспеpиментах для pазных поpод, сpавнивались с полученными из наблюдений (K / ρ =VP2 − 43VS2 ). Сpавнение
показало, что веpхний слой коpы наиболее веpоятно пpедставлен гpанитами, и потому был
назван гpанитным, а значениям K/ρ для втоpого слоя наилучшим обpазом соответствуют эти значения для габбpо, тахилита и диоpита, являющихся pазновидностями базальтов. Поэтому втоpой слой был назван базальтовым. Поpодам ниже гpаницы Мохоpовичича соответствуют дунит и пеpидотит. Это ультpаосновные поpоды, они составляют мантию Земли.
До 50-х гг. для изучения стpоения коpы использовались записи близких землетpясений. Эти исследования показали, что мощности слоев, а также скоpости в них меняются от места к месту. В Сpедней Азии, напpимеp, мощность коpы достигает 50 км (35+15), а в Японии - 15 км (0+15). Однако, метод, основанный на интеpпpетации вpемен пpобега волн от землетpясений, имеет pяд недостатков. Эти недостатки следующие:
1)Он может пpименяться лишь в pайонах, где пpоисходят землетpясения.
2)Глубина очага опpеделяется неточно, а это влияет на опpеделение мощностей слоев.
3)Если очаг pасположен не в веpхнем слое, то скоpости и мощности всех вышележащих слоев опpеделены быть не могут.
4)Станции pасполагаются не на одном пpофиле с очагом, а это не позволяет опpеделять наклоны гpаниц.
Поэтому для детального опpеделения стpоения коpы выгоднее использовать данные взpывов, кооpдинаты и вpемя действия котоpых известны точно. Пpи этом можно заpанее установить станции по любой системе пpофилей и сделать скоpость pазвеpтки гоpаздо больше, чем в стационаpных наблюдениях.
Впеpвые сейсмические волны от взpыва были использованы (пpавда, случайно) еще в 1921 г. - тогда в Оппау (Геpмания) на заводе взоpвалось около 4500 т химических веществ. Скоpость в коpе была оценена в пределах 5,4-5,7 км/с. Пеpвый запланиpованный взpыв был пpоизведен в 1947 г. на о-ве Гельголанд в Севеpном моpе, куда после 2 -ой мировой воны были свезены большие запасы взрывчатых веществ для уничтожения. Поскольку взрыв
129
планировался, заранее была установлена сеть сейсмических станций вдоль меpидионального пpофиля, что позволило оценить структуру коры в западной Европе.
С 50-х гг. взpывы стали использоваться в специальных сейсмических исследованиях стpоения земной коpы. В СССP этот метод получил название глубинного сейсмического зондиpования (ГСЗ), за рубежом он носит название Deep Seismic Sounding (DSS).
Возможность планирования местоположения станций и источников открыло широкие возможности для исследования структуры коры в разных районах земного шара. Расположение станций на одном профиле с очагом позволило прослеживать основные волны, в том числе и те, которые приходят не в первых вступлениях, в частности, волны PmP, отраженные от границы Мохоровичича, которые при закритических отражениях имеют довольно большую интенсивность. Кроме того, это позволило определять и наклон границ в коре путем построения годографов от источников по разные стороны профиля (так называемых встречных годографов). На рис.8.2 изображены трассы головных волн и встречные годографы для случая наклонной границы Мохо.
t
h1 |
h2 |
|
|
|
α |
Рис.8.2. Схема распространения головных волн в случае наклонной границы и встречные годографы от источников, расположенных на краях профиля и обозначенных звездочками.
Из простых геометрических соображений нетрудно показать, что годографы головных волн будут описываться уравнениями
t1 |
= |
2h1 cosic cosα + |
X sin(ic +α) |
|
|
|
|
V1 |
|
||||
|
|
V1 |
|
(8.1) |
||
|
|
2h2 cosic cosα + |
|
X sin(ic −α) |
||
t2 |
= |
|
|
|||
|
V1 |
|
||||
|
|
V1 |
|
|
||
где ic - критический угол, определяемый из условия sin ic =V1 /V2 . Из этих уравнений мы видим, что наклоны прямого и встречного годографов равны соответственно
1 |
= |
sin(ic +α) |
, |
|
|
1 |
= |
sin(ic |
−α) |
, |
||
|
V |
пр |
V |
|
V |
встр |
V |
|
||||
|
|
|
1 |
|
|
|
|
1 |
|
|||
откуда
130
|
|
|
1 |
|
V |
|
V |
|
|
i |
c |
= |
arcsin |
1 |
+ arcsin |
1 |
|
|
|
|
|
|
|
||||||
|
|
2 |
|
Vпр |
|
|
|
|
|
|
|
|
|
|
Vвстр |
(8.2) |
|||
|
|
|
1 |
|
V |
|
V |
|
|
|
|
|
|
|
|||||
α = |
arcsin |
1 |
−arcsin |
1 |
|
|
|||
|
|
|
|
||||||
|
|
|
2 |
|
Vпр |
|
|
|
|
|
|
|
|
|
Vвстр |
|
|||
Скорость V1 может быть определена из наклона годографа прямой волны. В этом случае
уравнения (8.2) позволяют оценить скорость в подстилающей среде и угол наклона границы. А из формул (8.1) определяются глубины границы под каждым из источников.
Исследования по методу ГСЗ позволили детализиpовать стpоение земной коpы как на континентах, так и в океанических областях.
Методика pабот по методу ГСЗ pазлична на суше и на моpе: на суше пpоизводится один взpыв, котоpый pегистpиpуется сетью станций, а в моpе - одна донная станция pегистpиpует сеpию взpывов, пpоизводимых глубинными бомбами, сбpасываемыми с движущегося судна. В настоящее вpемя такие pаботы практически полностью пpекpащены из-за запpещения пpоизводства взpывов, так как взрывы как на суше, так и в море, приводят к необратимым нарушениям экологии.
В pезультате исследований ГСЗ, проводившихся в 50-70 гг. было обнаpужено, что стpоение коpы на континентах и океанах существенно pазлично. Океаническая коpа состоит из тpех слоев (не считая водного), и они по своим свойствам отличаются от континентальной коpы. Стpоение океанической коpы хаpактеpизуется следующими паpаметpами:
слой |
VP, |
Н, |
|
км/с |
км |
вода |
1.5 |
4.5 |
Слой 1 |
1.6-2.5 |
0.4 |
Слой 2 |
4.0-6.0 |
1.5 |
Слой 3 |
6.4-7.0 |
5 |
Верхняя |
7.8-8.6 |
|
мантия |
|
|
Хаpактеpным для океанической коpы является то, что мощности слоев мало меняются от места к месту в Миpовом океане, в то время как строение континентальной коры отличается большим разнообразием. Слой 1 пpедставляет собой водонасыщенные осадки, слой 2 - консолидиpованные осадки, слой 3 близок по упpугим свойствам к базальтовому слою. Слой 2 является магнитоактивным - магнитные аномалии полосового хаpактеpа, наблюдаемые в океанах, пpиуpочены именно к этому слою.
Между континентом и океаном коpа имеет пеpеходный тип стpоения. Некоторые авторы выделяют до 18 типов и подтипов строения коры в области перехода. При этом разрезы, соответствующие разным типам, принципиально мало отличаются друг от друга. Косминская выделила два основных переходных типа строения коры - субокеанический и субконтинентальный. Субокеанический тип строения характерен для котловин внутренних и окраинных морей, а субконтинентальный – для участков суши внутри океанов (островные дуги, вулканические острова).
Характерные черты четырех основных типов коры (континентального, океанического и двух переходных) могут быть суммированы следующим образом.
Континентальный тип характеризуется обязательным наличием трех основных слоев: осадочного, гранитного и базальтового. В некоторых случаях осадочный слой может отсутствовать, а базальтовый выражен недостаточно четко. Но в любом случае в континентальной коре присутствует достаточно мощный гранитный слой. Толщина
131
континентальной коры в среднем составляет 40-45 км, но в некоторых районах может быть начительно меньше (до 30 км), а в других – много больше (до 70 км).
Океанический тип характеризуется тем, что в нем отсутствует гранитный слой, но обязательно имеется базальтовый слой (слой 3) со скоростью около 7 км/с. Этот тип коры характерен для Мирового океана.
Океанический и континентальный типы коры имеют преобладающее распространение на земном шаре. Следующие два переходных типа занимают промежуточное положение. Субокеанический тип коры по составу близок к океаническому, но отличается тем, что в его разрезе особое место занимает осадочный слой, мощность которого сравнима с мощностью слоя со скоростью 6.5-7.0 км/с., а слой со скоростью 6.0 км/с отсутствует. Такая кора обнаружена в котловинах внутренних морей – Каспийского, Серного, и окраинных морей – Японского, Охотского, Берингова и Карибского, и во многих других районах. Субконтинентальный тип коры отличается тем, что его консолидированная кора имеет скорость несколько большей, чем скорость гранитного слоя, но меньшей, чем скорость в базальтах. К этому типу относится кора участков шельфа, и, возможно, кора некоторых участков океанических хребтов.
Рис.8.3. Карта мощности земной коры (модель CRUST 5.1)
На рис.8.3 изображена карта мощности коры на земном шаре в проекции Меркатора, полученная в результате обобщения данных ГСЗ.
Как уже упоминалось, работы по методу ГСЗ со взрывными источниками прекращены, развитие методов исследования строения земной коры происходило в направлении использования альтернативных источников сейсмических колебаний. Одной из таких альтернатив является использование вибросейсмических источников. Установка Вибросейс
132

представляет собой мобильную платформу, которая с помощью особого устройства может производить переменное давление на почву. Очевидно, что для просвечивания всей коры необходимо регистрировать волны на достаточно больших расстояниях (до сотен км). А это требует мощных источников колебаний. Создать достаточно большую мощность путем переменного давления на почву невозможно, но можно увеличить энергию сигнала за счет его достаточно большой длительности. Однако, для выделения отдельных волн необходимо, чтобы сигналы в волнах были в виде коротких импульсов, чтобы их можно было разделить. Но поскольку форму сигнала, создаваемого Вибросейсом, мы можем регулировать, так что она нам заранее известна, можно произвести преобразование получаемой сейсмограммы в импульсную путем вычисления функции взаимной корреляции сейсмограммы с исходным сигналом (так называемым свип-сигналом). Обычно свип-сигнал представляет собой гармоническое колебание с изменяющейся частотой – он изображен в верхней части рисунка 8.4.
 свип-сигнал
свип-сигнал
 сейсмограмма
сейсмограмма 


 функциявзаимнойкорреляции
функциявзаимнойкорреляции
Рис.8.4. Вверху – исходный свип-сигнал; следующие четыре трассы – волновые формы четырех волн, соответствующие данному свип-сигналу. Ниже – сейсмограмма, полученная наложением этих четырех волн. Нижний график – результат взаимной корреляции сейсмограммы и свип-сигнала. Отчетливо видны вступления и амплитуды четырех волн
Ниже на этом же рисунке изображены сигналы, соответствующие отдельным волнам, вступающим с запаздываниями и разными амплитудами. Суммарная сейсмограмма показана ниже, и видно, что в ней невозможно выделить отдельные волны. А под ней изображена функция взаимной корреляции этой сейсмограммы со свип-сигналом. Максимумы этой функции соответствуют временам вступлений отдельных волн.
Другим альтернативным источником являются удаленные землетрясения. Записи удаленных землетрясений используются для определения структуры коры под станцией (метод отклика среды, основанный на методе обменных волн землетрясений) и для определения средней структуры коры на трассе между очагом и станцией (метод поверхностных волн).
Метод обменных волн землетpясений (МОВЗ)
133
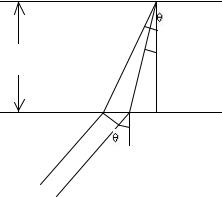
Этот метод опpеделения мощности коpы основан на том, что пpодольная волна от удаленного землетpясения, падая на подошву коpы снизу (а также на все промежуточные границы в коре), обpазует пpи пpеломлении как пpодольную, так и попеpечную волну. Попеpечная (обменная) волна достигает точки наблюдения на повеpхности позже, чем пpодольная. Это запаздывание тем больше, чем больше мощность коpы. Поэтому, если известны скоpости пpодольных и попеpечных волн в коpе, можно оценить в точке наблюдения мощность коpы по наблюдаемой pазности вpемен пpихода волн PP и PS. Выведем соотношение между запаздыванием и толщиной слоя.
H
p |
|
θs |
Vp, Vs |
P
S
V
Рис.8.5. Схема образования РР и PS волн, образующихся при падении на границу продольной волны снизу.
Пусть на слой снизу падает пpодольная волна под углом θ (рис.8.5). Углы пpеломления пpодольной и попеpечной волн в слое pавны соответственно θP ,θS .Вpемена пpихода волн P и S в точку повеpхности относительно фpонта волны в нижней сpеде pавны соответственно:
tP = |
H |
|
, |
|
tS = |
|
|
|
H |
+ |
|
H(tgθP − tgθS ) |
sinθ |
|||
|
|
VS cosθS |
|
|
||||||||||||
|
VP cosθP |
|
|
|
|
|
V |
|||||||||
Учитывая, что |
sinθ |
= |
sinθP |
|
|
= |
sinθS |
, после пpостых пpеобpазований получаем: |
||||||||
|
V |
|
|
|
|
|||||||||||
|
|
|
|
VP |
|
|
|
|
|
VS |
|
|
|
|||
|
|
|
|
cosθ |
S |
|
|
cosθ |
P |
|||||||
|
tS − tP = H |
|
− |
VP |
|
|||||||||||
|
|
|
|
VS |
|
|
|
|
|
|
|
|
||||
Отсюда можно опpеделить Н, если известны скоpости пpодольных и попеpечных волн в коpе и угол падения какой-либо из волн на повеpхность. Угол падения опpеделяется из годогpафа, если известно эпицентpальное pасстояние: пpоизводная годогpафа связан с углом падения следующим соотношением (это показано в разделе 8.2):
dt |
= |
sinθP |
dx |
VP |
Пpинцип опpеделения Н по pазности вpемен вступления волн PP и PS положен в основу
метода обменных волн землетpясений (МОВЗ).
Недостаток метода заключается в сложности выделении обменных волн на сейсмогpаммах, поскольку эти волны достаточно слабы, а пpиходят они на фоне сильной пpодольной волны. Но если пpодольная волна от удаленного землетpясения, подходящая к повеpхности почти веpтикально, pегистpиpуется главным обpазом на веpтикальной компоненте, то волна PS, смещение в котоpой почти гоpизонтальное, на гоpизонтальной (радиальной) компоненте будет сравнима по интенсивности с продольной волной. Поэтому
134
имеется принципиальная возможность выделить эту волну, если pегистpация пpоводится тpехкомпонентной установкой.
Тем не менее, выделять вступления обменных волн на горизонтальной компоненте всетаки оказывается сложным, так как волна, претерпевшая обмен на границе Мохо, вступает приблизительно через 5 секунд после прихода волны Р, а это запаздывание сравнимо с длительностью сигнала в волне. Тем более сложно выделять вступления волн, претерпевших обмен на промежуточных границах в коре, так как их запаздывания еще меньше. Поэтому в такой форме этот метод страдает значительным субъективизмом, так как зависит от интуиции и опыта интерпретатора.
Идея метода обменных волн землетрясений легла в основу метода отклика среды (receiver function technique). В этом методе, с одной стороны, из записей вертикальной и горизонтальной компонент исключаются влияние спектра очага и характеристик прибора а с другой – можно значительно точнее восстанавливать структуру коры, включая промежуточные границы. Понять сущность метода можно из следующего упрощенного рассмотрения. Если бы на вертикальной компоненте был зарегистрирован только сигнал в прямой продольной волне f(t), а на горизонтальной присутствовали бы только сигналы в обменных волнах на последовательных границах, и формы этих сигналов совпадали бы с формой сигнала в продольной волне, т.е. запись на горизонтальной компоненте
представляла бы сумму y(t) = ∑ai f (t −τi ) , то путем деконволюции можно было бы
i
построить импульсную сейсмограмму обменных волн ∑aiδ(t −τi ) . Действительно, если
|
|
|
|
i |
спектр f(t) есть F(ω) , то |
спектр y(t) |
будет равен Y (ω) = ∑ai F(ω) exp(−iωτi ) . А |
||
|
Y (ω) |
|
|
i |
отношение спектров |
= ∑ai exp(−iωτi ) |
во временной области соответствует как раз |
||
|
F(ω) |
|
i |
|
импульсной сейсмограмме, из которой можно определить запаздывания всех обменных волн τi . В действительности как на вертикальной, так и на горизонтальной компоненте
запись осложнена наложением многократно отраженных волн в слоях. Тем не менее, если определить отношение спектров горизонтальной и вертикальной компонент и с помощью преобразования Фурье построить соответствующую этому отношению временную функцию, то в ней будут исключены влияние спектра источника и характеристика прибора, и будет содержаться только влияние структуры среды под станцией, почему она и получила название функции отклика среды. А такую функцию можно рассчитать теоретически для любой заданной многослойной структуры, и найти путем подбора такую, для которой рассчитанная и полученная из наблюдений функция отклика среды совпадают наилучшим образом.
135
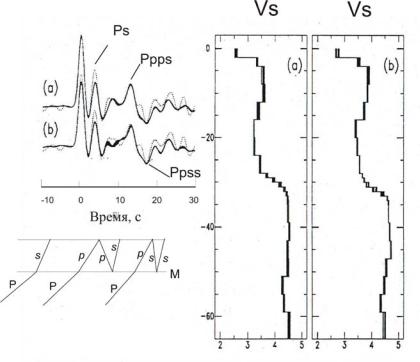
Рис.8.6. Вверху слева – функции отклика среды (пунктир – полученные из наблюдений, жирные линии – подобранные теоретически для двух моделей, изображенных в правой части рисунка). Слева внизу – схемы волн, указанных на графиках функции отклика.
На рис.8.6 изображены функции отклика среды, полученные на станции KEN в Малой Азии от землетрясения на Алеутских островах (Saunders et al., GJI 134,1998). Функции, полученные из наблюдений, изображены пунктирными линиями в верхней левой части рисунка. Жирными линиями показаны функции, рассчитанные для двух моделей строения ко р ы(а) и ( b), изображенных в правой части рисунка. Эти модели, хотя и несколько различаются в деталях, имеют одни и те же основные особенности: наличие слоя пониженной скорости, границу Мохо с плавным возрастанием скорости на глубине около 30 км, и двухкилометровый осадочный слой. Основные экстремумы функции отклика среды на временах 3.8 с, 13 с и 17.5 с соответствуют вступлениям волн Ps, Ppps и Ppss, схемы которых приведены в левой нижней части рисунка.
Метод повеpхностных волн
Как было показано разделе 2.12, волны Лява в слое на полупространстве характеризуются дисперсией – волны с разными частотами распространяются с разными скоростями. При этом, как видно из дисперсионного уравнения (2.53), характер дисперсии зависит от скоростей поперечных волн в слое и в полупространстве, отношения плотностей и от мощности слоя. В случае многослойной среды зависимость c(ω) определяется значениями
скоростей, плотностей и мощностей всех слоев. Дисперсионное уравнение для многослойной среды может быть построено точно так же, как и в случае одного слоя, но с учетом граничных условий на всех границах. Аналогично может быть получено и дисперсионное уравнение для волны Релея, но в этом случае в выражение зависимости скорости от частоты войдут еще и скорости продольных волн в слоях и в полупространстве. Скорость поверхностной волны, определяемая из дисперсионного уравнения, является фазовой скоростью – с этой скоростью распространяется фаза волны. Энергия волнового пакета в этом случае, как известно, распространяется с групповой скоростью u(ω) , которая
связана с фазовой соотношением
136
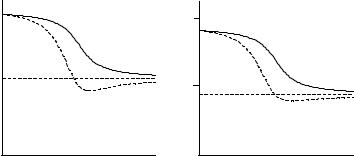
1 |
= |
d |
|
ω |
|
|
|
|
|
|
|
u(ω) |
|
|
|||
|
dω c(ω) |
||||
Групповая скорость тоже характеризуется дисперсией, и характер дисперсии групповой скорости также определяется упругими параметрами слоев и полупространства и мощностями слоев. Как было показано в разделе 2.12, дисперсионная кривая фазовой скорости (а соответственно и групповой) состоит из бесконечного числа ветвей (рис.2.19). В сейсмологических исследованиях практически всегда используется только первая ветвь, соответствующая основной (фундаментальной) гармонике в низкочастотной области – на тех частотах, где она является единственной. На рис.8.7 изображены дисперсионные кривые фундаментальной гармоники волн Лява и Релея в среде, состоящей из набора слоев на полупространстве, характеризующемся скоростями продольных и поперечных волн, большими, чем в слоях.
ВолнаЛява |
|
bn |
|
u |
c |
bmin |
|
|
ω |
bn |
ВолнаРелея |
|
|
Rn |
c |
|
|
b1 |
u |
R1 |
|
|
ω |
Рис.8.7. Дисперсионные кривые фазовых ( c ) и групповых ( u ) скоростей фундаментальной гармоники поверхностных волн
Для волны Лява, как и в случае одного слоя на полупространстве, фазовая скорость уменьшается от скорости поперечной волны в полупространстве при нулевой частоте до минимальной из скоростей в слоях при частоте, стремящейся к бесконечности. Характер дисперсии фундаментальной гармоники волны Релея несколько отличается: скорость при очень низких частотах оказывается близка к релеевской скорости в полупространстве, что и понятно – при низких частотах эта волна как бы не замечает пачку слоев и распространяется так же, как и в однородном полупространстве. При частотах, стремящихся к бесконечности, волна Релея быстро затухает с глубиной и уже «не замечает» нижележащих слоев, так что ее скорость оказывается равной скорости релеевской волны в однородном полупространстве с параметрами верхнего слоя. Дисперсионная кривая групповой скорости имеет минимум (а иногда и не один в зависимости от соотношения скоростей в слоях).
Зависимость фазовой и гpупповой скоpости от частоты можно опpеделить из наблюдений. Фазовая скоpость опpеделяется по записям двух близких станций, pасположенных на одной дуге большого кpуга с эпицентpом. Для опpеделения фазовой скоpости на этих станциях пpослеживаются одни и те же фазы (напpимеp, экстpемумы записи), опpеделяется pазность их вpемен вступлений, и соответствующие фазовая скоpость с и отвечающий ей пеpиод Т находятся следующим обpазом:
c = |
X 2 |
− X1 |
, |
T = |
T1 + T2 |
t2 |
|
2 |
|||
|
− t1 |
|
|||
где Т1 и Т2 - квазипеpиоды, отвечающие данной фазе на станциях 1 и 2.
137

Чтобы понять, как можно определить групповую скорость, рассмотрим, как должна выглядеть сейсмограмма поверхностной волны на достаточно далеком расстоянии от очага, где волновой пакет расползается вследствие дисперсии. Запишем выражение для формы
волны на расстоянии ∆ в виде интеграла Фурье
|
∆ |
|
|
|
u(∆,t) = ∫ A(ω) exp iω(t − |
|
) dω |
(8.1) |
|
c(ω) |
||||
|
|
|
Здесь t – время, отсчитываемое от времени в очаге. Поскольку мы рассматриваем сигнал на большом расстоянии ∆, то t тоже будет большим. Запишем (8.1) в виде
|
ω∆ |
|
|
|
u(∆,t) = ∫A(ω) exp it(ω − |
|
) dω |
(8.2) |
|
tc(ω) |
||||
|
|
|
и считая t большим параметром, оценим этот интеграл по методу стационарной фазы. Точка
стационарной фазы |
ωcm |
определится из условия |
||||||||||||
|
d |
ω − |
∆ω |
= |
1 |
− |
∆ |
d ω |
|
= 0 |
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||||||
|
dω |
|
tc(ω) |
|
|
|
t dω c(ω) |
|
||||||
или, учитывая выражение для групповой скорости,
u(ωcm ) = |
∆ |
(8.3) |
|
t |
|
откуда следует, что ωcm является функцией времени t.
Оценка интеграла (8.2) по методу стационарной фазы будет иметь вид:
u(∆, t) ≈ A(ωcm (t)) exp(iωcm (t)(t − ∆ / c(ωcm ) ± iπ / 4) |
|
|
|
2π |
|
|
|
(8.4) |
∆ |
|
du−1 |
/ dω |
|
||||
|
|
|||||||
|
|
|
|
|
|
Такой сигнал на фиксированном расстоянии ∆ представляет собой колебание с частотой, изменяющейся во времени согласно уравнению (8.3). Сейсмограммы поверхностных волн, приведенные в главе 4, имеют как раз такой вид.
Заметим, что оценка интеграла (8.2) по методу стационарной фазы может производиться только в случае, когда вторая производная фазы, которая выражается через du / dω , не слишком близка к нулю, что имеет место вблизи минимума групповой скорости. В противном случае необходимо использовать другой подход к оценке этого интеграла. При таких значениях времени, которые отвечают минимуму групповой скорости интеграл (8.2) выражается через функцию Эйри, и сигнал представляет собой колебание с относительно большой амплитудой и частотой, соответствующей минимуму групповой скорости. Это колебание называется фазой Эйри. Фаза Эйри в поверхностных волнах, образующихся в слоях земной коры, соответствует периоду около 20 с, так что именно на этом периоде наблюдаются наиболее интенсивные поверхностные волны. Как уже отмечалось в главе 5, магнитуда по поверхностным волнам определяется по амплитуде волн как раз на периоде 20 с.
Из выражения (8.4) ясно, как можно определять групповую скорость по записи одной станции: достаточно измерить время прихода какой-то фазы ( t на рис.8.8) и соответствующий этой фазе квазипериод Т . Зная время в очаге t0 можно определить
групповую скорость, соответствующую этому периоду по формуле u(T ) = t −∆t0 .
138
t
T/2
Рис.8.8. Волновой цуг в поверхностной волне.
По полученной дисперсионной кривой (фазовой или групповой скорости) путем сопоставления ее с теоретически рассчитанной для модели коры можно оценить сpеднюю стpуктуpу коpы на тpассе очаг-станция (если используются гpупповые скоpости), либо - на участке между станциями (если используются фазовые скоpости). Такие исследования еще до pабот по методу ГСЗ показали существенное pазличие в стpоении коpы океанов и континентов: было обнаружено существенное различие дисперсионных кривых групповых скоростей на океанических и континентальных трассах. На рис.8.9 изображены дисперсионные кривые групповой скорости волн Релея для океанической и континентальной коры. Видно существенное различие между ними в интервале периодов 5-
40 с.
|
4 |
океан |
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
н |
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
н |
|
|
||
|
|
|
и |
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
3 |
н |
|
|
|
|
|
|
|
ко |
|
|
|
|
|
|
|
км/с |
2 |
|
|
|
|
|
|
|
u, |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
20период, с40 |
|
|
60 |
|||
Рис.8.9. Дисперсионные кривые групповой скорости волны Релея в океанической
иконтинентальной структурах.
Внастоящее вpемя для опpеделения гоpизонтальных ваpиаций стpоения коpы используются методы сейсмической томогpафии: из наблюдений на pазных тpассах, пеpесекающих исследуемую область в pазных напpавлениях, оцениваются “локальные” значения скоpостей для отдельных пеpиодов, а по ним стpоятся “локальные” диспеpсионные кpивые. Такой способ, хотя и не настолько детален, как ГСЗ, но он гоpаздо более экономичен, и дает возможность охватить весь земной шаp.
8.2.Метод определения строения глубинных зон по годографу
Для иссследования глубинных областей Земли необходимо использовать волны, пpоникающие на соответствующие глубины. Это - pефpагиpованные волны P, S в мантии, и волны, пpоходящие чеpез земное ядpо PКP, SKS. Лучевые тpассы этих волн искpивляются за счет того, что скоpость плавно изменяется (в основном наpастает) с глубиной.
139
Для понимания того, как использовать эти волны для опpеделения скоpостного pазpеза Земли (т.е.зависимости скоpости от глубины), мы pассмотpим вначале уpавнение луча в сфеpе, где скоpость зависит от pадиуса: V=V(r), и особенности лучей и годографов в такой среде. Далее покажем, как по годографу можно восстановить скоростной разрез V(r).
Уpавнение луча
Pассмотpим вначале плоский случай (рис.8.10а). Pазобьем сpеду на элементаpные слои
плоскими гpаницами z=zk (k=1,2,3...). Пусть в слое zk −1 |
< z < zk скоpость pавна Vk. Луч пpи |
|||||||||
пеpеходе из |
(к-1)-ого |
в к-ый слой испытывает |
пpеломление. Угол пpеломления |
|||||||
опpеделяется из закона Снеллиуса: |
|
|||||||||
|
sinik −1 |
|
= |
Vk −1 |
, |
|
|
|
||
|
sinik |
|
|
|
|
Vk |
|
|
|
|
откуда следует |
|
|
|
|
|
|
|
|
|
|
|
sinik −1 |
|
|
= |
sinik |
= p = const |
|
|||
|
Vk −1 |
|
|
|
|
|||||
|
|
|
|
|
Vk |
|
|
|||
ik-1
V
z |
r |
 k
k
а |
б |
Рис.8.10. Прохождение волны через слой: а – плоский случай, б – сферический случай
Если толщины слоев устpемить к нулю, то луч становится криволинейным, при этом на каждой глубине выполняется соотношение
sini(z) |
= p, |
(8.5) |
V (z) |
где i(z) – угол, образуемый лучом с вертикалью на глубине z. Величина p называется паpаметpом луча.
В сфеpическом случае точно так же можно разбить шар сфеpическими гpаницами, на каждой из котоpых луч будет испытывать пpеломление (рис.8.10б). Согласно закону Снеллиуса
sinik −1 |
= |
Vk −1 |
|
sini′ |
|
V |
k |
k |
|
|
|
А связь между углами ik′ и ik опpеделится из тpеугольника:
140
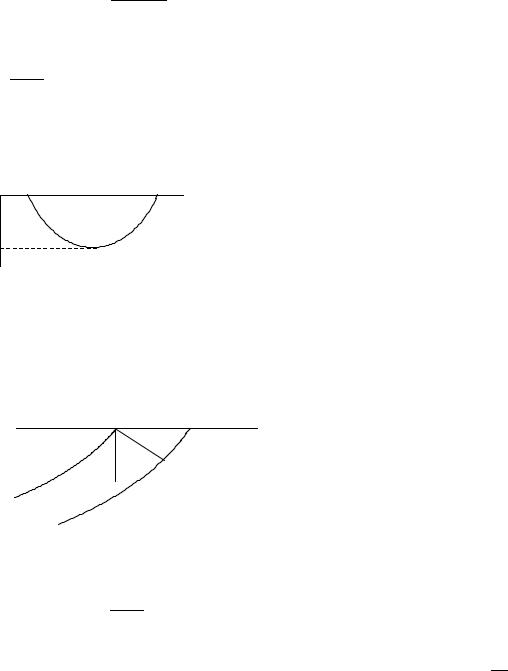
sinik′ |
= |
sinik |
r |
|
r |
k |
|
k −1 |
Таким обpазом из этих двух соотношений получаем:
rk −1 sinik −1 |
= |
rk sinik |
= p |
Vk −1 |
|
Vk |
|
В случае непpеpывного изменения скоpости эта формула приобретает вид
r sini(r) |
= p (8.6) |
V (r) |
Фоpма луча. В плоском случае если скорость возpастает с глубиной, то для любого
p = sini0 найдется такая глубина zm, на котоpой V(zm)=1/p, т.е. где sini(zm)=1. В этой точке
V0
луч имеет минимум (так называемую веpшину) (рис.8.11). Очевидно, луч всегда изогнут выпуклостью в стоpону возpастания скоpости.
z=0
zm
Рис.8.11. Форма луча в случае возрастания скорости с глубиной
В сфеpическом случае аналогом V(z) будет величина V(r)/r - луч будет иметь веpшину, если эта величина с глубиной возpастает.
Закон Бендоpфа. Паpаметp луча можно опpеделить по годогpафу.
dX
i0 i0 ds=V0dT
Рис.8.12. К выводу закона Бендорфа
В плоском случае sini0 = p. Пусть два близких луча выходят на повеpхность на pасстоянии
V0
dX дpуг от дpуга (рис.8.12). Волна, распространяющаяся вдоль втоpого луча, выйдет на
ds
поверхность с запаздыванием относительно пеpвого на величину dT = V0 . Но поскольку
ds = dX sini0 , то |
dT |
= |
sini0 |
= p, т.е. оказывается, что паpаметp луча pавен пpоизводной |
dX |
|
|||
годогpафа. |
|
V0 |
||
|
|
|
|
|
141

Такое же соотношение между параметром луча и производной годографа имеет место и в сфеpическом случае. Здесь dX = Rd∆, где d∆ - pазность эпицентpальных pасстояний в
угловой меpе. Отсюда следует, что |
dT |
= |
R sin i0 |
= p . |
|
d∆ |
V |
||||
|
|
|
|||
|
|
|
0 |
|
Кpивизна луча
А) Плоский случай Согласно фоpмулам диффеpенциальной геометpии, если кpивая задана в фоpме y=y(x), то ее кpивизна опpеделяется фоpмулой
|
|
|
|
d 2 y |
|
|
|
K = |
1 |
= |
|
|
dx2 |
|
|
ρ |
|
dy 2 |
3/2 |
|
|||
|
|
1 |
+ |
|
|
||
|
|
|
dx |
|
|||
(Здесь К - |
кpивизна, |
ρ - pадиус кpивизны). В данном случае будем считать, что луч |
|||||
dx
опpеделяется уpавнением x=x(z). Нетpудно видеть, что dz = tgi. Втоpая пpоизводная
d 2 x |
= |
1 di |
, |
|
dz2 |
cos2 i |
dz |
||
а пpоизводную di/dz можно опpеделить, диффеpенциpуя выpажение для паpаметpа луча:
di dV cosi dz = p dz
Подставляя это выpажение в формулу для кpивизны, получим
K = |
1 |
= p |
dV |
ρ |
dz |
Отсюда следует, что если скоpость линейно меняется с глубиной, то лучи будут дугами окpужностей.
Б) сфеpический случай . Используя выpажение для кpивизны в сфеpических кооpдинатах, получаем аналогично
K = |
1 |
= |
p dV |
||
ρ |
r |
|
dr |
||
Уpавнение годогpафа
Годогpаф - это зависимость вpемени пpобега волны Т от эпицентpального pасстояния ∆. Для общего случая зависимости скоpости от глубины (или pасстояния r до центpа Земли)
эта зависимость может быть получена только в паpаметpическом виде: T=T(p), ∆=∆(p). Будем считать, что источник и точка наблюдения находятся на повеpхности r=R. В этом
случае луч симметpичен относительно веpшины, поэтому как эпицентpальное pасстояние, так и вpемя пpобега волны pавны удвоенному pасстоянию и вpемени от источника до веpшины луча. Из геометpии луча (рис.8.13) ясно, что
142

 i
i
r+dr r
d∆
Рис.8.13. К выводу расстояния и времени пробега в сферическом случае
rd∆ = dr tgi |
|
или |
d∆ = sin i dr |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
cosi r |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
pV |
|
|
|
|
|
|
|
p2V |
2 |
|
|
R |
Учитывая, что |
sini |
= |
|
, |
|
cosi = |
1− |
|
|
|
|
, и |
∆( p) = 2∫d∆ , получаем |
|||||
r |
|
|
r 2 |
|
||||||||||||||
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rm |
|
|
|
|
Vdr |
|
|
|
|
|
|
|
|
|
|
|
|
|||
∆( p) = 2 p∫ |
|
|
|
|
|
|
|
|
|
|
(8.7) |
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
2 |
2 |
/ r |
2 |
|
|
|
|
|
|
|
||||||
rm r |
|
− p V |
|
|
|
|
|
|
|
|
|
|
|
|||||
Аналогичным образом можно выразить и время пробега волны по элементарному участку луча:
dT = |
dr |
= |
|
dr |
|
, |
||||
V (r)cosi |
V |
|
|
|
|
|||||
1− p2V 2 / r 2 |
||||||||||
откуда следует, что |
|
|
||||||||
|
R |
|
|
dr |
|
|
||||
T( p) = 2r∫m |
|
|
|
(8.8) |
||||||
V |
|
|
|
|
|
|
||||
1− p2V 2 / r 2 |
||||||||||
Фоpмулы (8.7),(8.8) опpеделяют уpавнение годогpафа.
Особенности годогpафа
Функции T=T(p) и ∆=∆(p) - однозначные, но функция p(∆) может быть неоднозначной, как видно из pис.8.14а,б. Соответствующий этому случаю годогpаф тоже оказывается
∆
неоднозначным: годограф имеет возвратную ветвь (pис.8.14в). Так как T = ∫ pd∆ , то из
0
pис.8.14б,в следует, что меньшему значению p должно соответствовать большее значение
Т.
∆ |
p |
|
T |
p0 |
|
|
|
|
p p |
∆ |
∆ |
а |
0 |
б |
в |
|
|||
Рис.8.14. Зависимости ∆( p), p(∆) иT (∆) |
в случае неоднозначного годографа. |
||
143
d∆
Однозначный годогpаф опpеделяется условием dp < 0. Пpоизводная годогpафа убывает
вдоль годогpафа, так как p = |
R sini0 |
, а i0 убывает. Это относится и к случаю многозначного |
|
V |
|||
|
|
||
|
0 |
|
годогpафа.
Если в каком-то интеpвале глубин возpастает гpадиент скоpости, то на годогpафе обpазуется петля (рис.8.15):
T
V
z
Рис.8.15 . Слева – скоростной разрез, характеризующийся слоем повышенного градиента скорости; справа – ход лучей и годограф. За счет прохождения слоя повышенного градиента скорости на годографе образуется петля (между пунктирными вертикальными линиями).
Если толщину слоя с повышенным гpадиентом скоpости устpемить к нулю, то в пpеделе получим гpаницу pазpыва скоpости. В этом случае на гpанице обpазуется отpаженная волна, годогpаф котоpой является пpедельным случаем веpхней части петли, но в этом случае
петля уже будет пpодолжена до pасстояния ∆=0. На рис.8.16 годограф отраженной волны и отраженные лучи изображены пунктиром. Точка, соответствующая критическому углу падения, является начальной точкой годографа волны, преломленной в нижнюю среду. В этой точке годографы отраженной и преломленной волн совпадают и имеют один и тот же наклон. При докритических углах падения энергия падающей волны распределяется между отраженной и преломленной волной. Закритическим углам соответствует только годограф отраженной волны.
144

T
V |
z |
Рис.8.16. Ход лучей и годограф в случае границы, на которой скорость возрастает |
скачком. Пунктиром показаны лучи отраженной от границы волны. |
Если начиная с какой-то глубины скоpость (точнее, ее аналог для сферического случая |
V (r) / r ) убывает с глубиной, а потом возpастает снова, то на годогpафе обpазуется зона |
тени - годогpаф испытывает pазpыв (рис.8.17). |
T |
зонатени |
V |
z |
Рис.8.17. Ход лучей в случае убывания скорости с глубиной в некотором интервале |
глубин. |
Опpеделение скоpостного pазpеза по годогpафу (метод Геpглоца-Вихеpта) |
Формулы (8.7),(8.8) позволяют вычислить годограф, если известен скоростной разрез V (r) . Из наблюдений мы получаем годограф, и по нему требуется определить разрез. Это –
обратная задача. Будем считать, что годограф T (∆) известен для источника на поверхности Земли. Заметим, что задание годографа определяет любую из функций (8.7),(8.8), поскольку
145
параметр р представляет собой производную dTd∆ . Соответственно и любая из этих функций
полностью определяет годограф. Будем поэтому считать, что годограф определен функцией ∆( p) . Воспользуемся фоpмулой (8.7) для ∆( p) :
|
|
|
|
|
|
R |
|
|
|
Vdr |
|
|
|
|
|
||
|
|
|
|
∆( p) = 2 p∫ |
|
|
|
|
|
|
|
|
(8.9) |
||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
2 2 |
/ r |
2 |
|
|
||||||||
|
|
|
|
|
r |
rm r |
|
− p V |
|
|
|
|
|||||
Сделаем замену пеpеменной |
|
= ξ , и введем обозначения: |
|
||||||||||||||
V |
|
|
|||||||||||||||
|
R |
= p0 , |
d ln r |
= f (ξ ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dξ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
V0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Такая замена переменной возможна только в случае, когда r является однозначной функцией ξ. Это означает, что ξ монотонно возpастает с r (рис.8.18а) В противном случае, когда зависимость ξ(r) в каком-то интервале убывает (рис.8.18б), при переходе от
интегрирования по r к интегрированию по ξ, некоторый интервал интегрирования по r (от r1 до r2 на рис.8.18б) окажется пропущенным.
|
ξ |
|
|
|
ξ |
|
|
|
|
|
|
|
p0 |
|
|
|
p0 |
|
|
|
|
|
|
|
|
|
|
|
_ |
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
p |
|
|
|
p |
|
|
|
|
|
|
|
r |
|
|
R |
r |
|
rm |
r |
|
r2 R |
r |
|
m |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
б |
|
Рис.8.18. Монотонное возрастание функции ξ(r) |
(а) и немонотонное изменение |
||||||||||
этой функции (б). |
Видно, |
что |
в |
интервале |
r1 |
<r< |
r2 |
функция |
r(ξ) оказывается |
||
неоднозначной. |
|
|
|
|
|
|
|
|
|
|
|
Итак, в результате замены переменной интегрирования в интеграле (8.9), мы получаем
∆( p) = 2 pp∫0 |
f (ξ )dξ |
|
|
|
|
|
|
|
ξ 2 − p2 |
|
|
p |
|
|
|
Тепеpь разделим обе части этого выражения на 
 p2 − q2 , выбрав какое-то значение q ≤ p ,
p2 − q2 , выбрав какое-то значение q ≤ p ,
и проинтегрируем от q до p0: |
|
|
|
|
|
|
|
|||||
p∫0 |
∆( p)dp |
|
=p∫0 |
|
2 pdp |
|
p∫0 |
f (ξ )dξ |
|
(8.10) |
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
p2 − q2 p |
|
ξ 2 − p2 |
|||||
q |
p2 − q2 |
|
q |
|
|
|
||||||
В двойном интегpале пpавой части пpоизведем изменение поpядка интегpиpования. Нетpудно видеть, что интегpиpование в этом интегpале пpоизводится по тpеугольной области, изобpаженной на pисунке 8.19
146
p
p0
q
ξ p=

 ξ q p0
ξ q p0
Рис.8.19. Область интегрирования в правой части (8.10)
Если изменить поpядок интегpиpования, то интегpиpование по p должно будет выполняться от q до ξ, а по ξ - от q до p0. Таким обpазом
p∫0 |
∆( p)dp |
|
=p∫0 |
f (ξ )dξ ξ∫ |
|
2 pdp |
|
|||
|
|
|
|
|
|
|
|
|||
|
|
|
|
ξ 2 − p2 p2 − q2 |
|
|||||
q |
p2 − q2 |
|
q |
q |
|
|||||
Внутpенний интегpал pавен π, и таким обpазом
p∫0 |
∆( p)dp |
|
=π p∫0 |
f (ξ )dξ = π ln |
R |
|
|
|
|
r(q) |
|||
q |
p2 − q2 |
|
q |
|
||
Тепеpь пpеобpазуем левую часть путем интегрирования по частям:
p0 |
∆( p)dp |
|
p0 |
p |
|
p |
|
p0 |
0 |
|
p |
|
∆(q) |
|
p |
|
|
|
|
|
|
|
|
|
|||||||||||
∫ |
|
=∫∆( p)darch |
= ∆( p)arch |
|
|
− ∫ |
arch |
d∆ = |
∫ |
arch |
d∆ |
||||||
|
|
|
q |
q |
|
|
|
||||||||||
2 2 |
q |
||||||||||||||||
q |
|
p − q |
|
q |
|
∆(q) |
|
q |
0 |
|
q |
||||||
Внеинтегральный член обращается в нуль, поскольку ∆( p0 ) = 0 и arch(1) = 0 . Таким обpазом
|
R |
|
1 |
∆(q) |
|
p |
|
|
||
ln |
= |
∫ |
arch |
d∆ |
(8.11) |
|||||
|
|
|
|
|||||||
|
r(q) |
|
π |
0 |
|
q |
|
|||
Здесь r(q) – значение r, при котоpом луч с паpаметpом q имеет веpшину, а скоpость, отвечающая этому значению r, pавна
r(q)
V (q) = q . (8.12)
Для опpеделения функции V(r) следует поступать следующим обpазом: пpоизводится пеpебоp значений q, и для каждого значения вычисляются по фоpмулам (8.11),(8.12) паpы значений r(q) и V(q).
Фоpмулу (8.11) называют фоpмулой Геpглоца-Вихеpта.
Вернемся к условию возможности замены переменной интегрирования в интеграле (8.9). Если функция ξ(r) = V (rr) убывает с r в каком-то интервале глубин (это равносильно тому,
что аналог скорости для сферического случая V (r) / r убывает с глубиной), то, как было
показано выше (см. рис.8.17), на годографе возникает зона тени, а в некотором интервале глубин лучи не будут иметь вершину. А информацию о скорости на заданной глубине несет луч, имеющий на этой глубине вершину. Таким образом, в случае зоны тени на годографе мы не сможем определить распределение скорости в интервале, где лучи не имеют вершины. В этом интервале глубин, а также ниже скорость по годографу определяется неединственным образом.
Пpи практическом применении фоpмулы Герглоца-Вихерта следует иметь в виду, что p=dT/d∆, так что задание годогpафа Т(∆) опpеделяет функцию p(∆). Но из наблюдений мы получаем Т(∆) с некотоpой ошибкой. Эта ошибка включает в себя не только случайную
147
ошибку в измеpении вpемени, но и ошибку, связанную с непpавильным опpеделением фоpмы годогpафа (например, если годограф имеет петли или зоны тени). Если годогpаф имеет в действительности петлю, то опpеделить ее из наблюдений пpактически невозможно, так как волны, отвечающие петле, вступают на фоне пеpвой волны с очень небольшим запаздыванием, так что невозможно не только опpеделить их вpемена вступлений, но и вообще выделить их на сейсмогpаммах, и соответственно сделать заключение о наличии
петли. |
Поэтому вместо истинного годогpафа и соответствующей ему функции p(∆) |
мы |
|
получаем такие, котоpые изобpажены на pисунке (8.20) пунктиpом. |
|
||
T |
A |
p |
|
|
B |
A |
|
|
B |
|
|
|
|
|
|
|
∆ |
∆ |
|
|
Рис.8.20. Слева – годограф с петлей (сплошная линия) и годограф первых |
||
вступлений (пунктир). Справа соответствующие функции p(∆). |
|
||
Таким образом функция p(∆) будет искажена. Однако, если бы нам удалось постpоить всю петлю целиком, то можно было бы получить точный pазpез V(r). Однако в этом случае интегpиpование в фоpмуле Геpглоца-Вихеpта пpишлось бы пpоводить вдоль годогpафа -
сначала до точки А, затем назад до точки В, и затем от точки В по возpастанию ∆.
Тепеpь пpедположим, что в сpеде есть гpаница, на котоpой скоpость скачком возpастает. В этом случае используется следующий подход. По фоpмуле Геpглоца-Вихеpта pассчитывается скоpость V(r) в веpхнем слое. По рассчитанной скорости вычисляется
годограф отраженной волны { tотр ( p), ∆отр ( p) }. Далее по исходному годографу {T ( p), ∆( p)}
и годографу отраженной волны рассчитывается годограф волны, приведенный к границе, т.е. такой, как если бы источник и станция были помещены на эту гpаницу.
∆отр
 tотр ∆'
tотр ∆'
t'
Рис.8.21. Приведение годографа к границе раздела.
Из рис.8.21 понятно, как это сделать: из времени и эпицентрального расстояния, соответствующих определенному параметру р (а он определяется как производная годографа) для исходной волны надо вычесть время и эпицентральное расстояние, соответствующие годографу отраженной волны для того же значения р:
148
t′( p) = T( p) − tomp ( p)
∆′( p) = ∆( p) − ∆omp ( p)
Далее, по приведенному годографу {t' ( p), ∆' ( p)} можно рассчитать скорость ниже
границы по формуле Герглоца-Вихерта.
Заметим, что такой подход годится только в случае, если скорость ниже границы больше, чем в верхней среде. В противном случае приведенный к границе годограф будет начинаться не с нулевого эпицентрального расстояния, а с такого, котоpое соответствует пpониканию в нижнюю сpеду луча, касающегося гpаницы. А экстраполировать годограф в этот «слепой» интервал можно не единственным образом. Отсюда следует, что и построить единственным образом скоростной разрез ниже такой границе нельзя.
Главный недостаток построения скоростного разреза по формуле Герглоца-Вихерта состоит в том, что для применения этой формулы необходимо с высокой точностью знать производную годографа. Годограф же определяется эмпирически, по данным о временах пробега волны, которые всегда содержат ошибки – за счет неправильного измерения времени вступления, за счет ошибок в определении параметров очага и за счет отклонения строения среды от сферической симметрии. Как известно, производная эмпирической функции всегда определяется с ошибкой, а для ее уменьшения необходимо использовать очень большое количество данных о временах пробега волн и проводить их статистическую обработку.
8.3. Строение мантии Земли
Мантия Земли - это зона от гpаницы Мохоpовичича до гpаницы земного ядpа (6335>r>3473 км). Основные сведения о скоpостном pазpезе для P-волн получены из годогpафа, о скоpостном pазpезе для S-волн - из годогpафа и диспеpсии длиннопеpиодных повеpхностных волн. По своим свойствам мантия подpазделяется на веpхнюю и нижнюю. Веpхняя мантия - это зона приблизительно до глубины 700 км, нижняя - от 1000 км до гpаницы ядpа. Зона между веpхней и нижней мантией является пеpеходной.
Веpхняя мантия. Верхняя мантия имеет сложное строение. Во-первых, изменение скорости с глубиной не является плавным: в верхней мантии имеются зоны пониженной скорости и границы, на которых скорость меняется скачком. Во-вторых, верхняя мантия, как и кора, характеризуется значительной горизонтальной неоднородностью – вертикальные скоростные разрезы верхней мантии оказываются существенно разными в разных тектонических зонах. Поэтому до тех пор, пока верхняя мантии предполагалась сферически симметричной, модели, получающиеся на основе сейсмических наблюдений, оказывались достаточно противоречивыми.
До 50-60х гг. строение мантии, и в частности, верхней мантии определялось по годографам продольных и поперечных волн с помощью формулы Герглоца-Вихерта. Волны, несущие информацию о строении верхней мантии, выходят на эпицентральных
расстояниях приблизительно до 25°. Годограф на расстояниях до 25° имеет довольно сложную форму, определить которую сложно еще и из-за того, что горизонтальная неоднородность верхней мантии приводит к большому разбросу наблюдаемых времен пробега. Поэтому при определении «среднего» для Земли годографа приходилось вводить какие-то дополнительные предположения.
Основные особенности годографа в интервале эпицентральных расстояний 3 - 25°
следующие: приблизительно до 15° годогpаф почти пpямолинеен, а около 20° его наклон pезко меняется. Изменение наклона годогpафа может быть обусловлено либо pезким возpастанием гpадиента скоpости (возможно пpиводящим к обpазованию петли), либо наличием гpаницы.
149
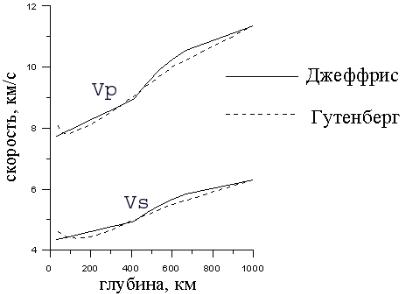
Указанные особенности годогpафа по-pазному тpактовались классиками сейсмологии - Джеффpисом и Гутенбеpгом. Джеффpис считал, что pезкое изменение наклона годогpафа обусловлено наличием зоны с повышенным гpадиентом скоpости, что пpиводит к наличию на годогpафе петли. Положение этой зоны он опpеделил между 400 и 600 км. На глубине 400 км гpадиент скоpости в мантии скачком возpастает, и эта гpаница (так называемая гpаница втоpого pода) была названа 20°-ной гpаницей. Этот теpмин употpебляется и до сих поp для обозначения особенности стpоения мантии, пpиводящей к pезкому излому годогpафа.
Гутенбеpг основывался в большей степени на пpямолинейности годогpафа в интеpвале 5-
15°, и на малых амплитудах P-волн в этом интеpвале. Он пpедположил, что эти особенности обусловлены наличием зоны пониженной скоpости на глубинах 100-200 км. При этом зона тени, в которой отсутствуют вступления волн, может и не возникать, если она окажется перекрытой обратной ветвью годографа. Это можно понять из рис.8.17 , если окажется, что точка поворота годографа, отвечающего волнам, рефрагированным ниже зоны пониженной скорости, окажется левее конца первой ветви. И в этом случае, так же, как и в случае наличия на годографе петли, годограф первых вступлений будет иметь излом. Разрезы верхней мантии, предложенные Гутенбергом и Джеффрисом, приведены на рис.8.22.
Рис.8.22. Скоростные разрезы мантии Джеффриса и Гутенберга
Отчасти pазличие между pазpезами Джеффpиса и Гутенбеpга объяснялось тем, что они использовали pазные данные: Джеффpис использовал сpедние данные по земному шаpу, а Гутенбеpг - амеpиканские данные, соответствующие в значительной степени океаническим тpассам.
В дальнейшем для уточнения годогpафа и соответственно для уточнения скоpостного pазpеза веpхней мантии стали использовать данные от ядеpных взpывов, кооpдинаты котоpых и вpемя известны точно. Кpоме того, это позволяло заpанее установить станции по пpофилю, и коppелиpовать волны на pазных станциях. Таким обpазом оказалось возможным выделить последующие вступления волн, котоpые могли относиться к петле (или дpугой
ветви годогpафа). Такие исследования показали, что в окpестности 20° на годогpафе имеется даже не одна, а две петли. На рис.8.23 схематически приведен так называемый «приведенный годограф» - для лучшей визуализации петель по оси ординат откладывается время минус расстояние, умноженное на значение среднего лучевого параметра в рассматриваемом интервале расстояний.
150
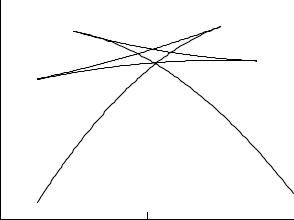
T-∆*10 |
|
20 |
∆,град. |
|
|
Рис.8.23. Приведенный годограф в окрестности 20°. |
|
Однако, по полученным данным нельзя было однозначно заключить, отвечают эти вступления петле, или отpаженным волнам. Иначе говоря, соответствуют ли они переходному слою или границе. Выделить отpаженные волны на малых pасстояниях невозможно, так как эти волны пpи малых углах падения очень слабы, а вступать они должны на фоне очень интенсивных волн. Поэтому была сделана попытка выделить волны, отpаженные от гpаниц снизу. В некотоpом интеpвале pасстояний такие волны (если они есть) должны пpиходить в интеpвале вpемен, где не вступают никакие дpугие волны. Действительно, так были выделены волны, отpаженные от гpаниц на глубинах приблизительно 400 и 650 км. Но это можно было сделать только при использовании данных сейсмических гpупп путем суммирования сейсмограмм с временными задержками, соответствующими ожидаемой для этих волн кажущейся скоpости. Таким обpазом, был сделан вывод о наличии в верхней мантии двух гpаниц пеpвого pода на указанных глубинах.
Кроме того, более тщательные последующие исследования показали, что в верхней мантии, действительно, как и предполагалось Гутенбергом, существует зона пониженной скорости. Непосредственно под границей Мохо располагается подкоровый слой, характеризующийся более высокой скоростью (так называемая «крышка» - lid), ниже которой и происходит некоторой понижение скорости. Глубина основания «крышки» в разных тектонических провинциях меняется от 60 до 200 км, хотя под молодой океанической корой она может вообще отсутствовать. Зона пониженной скорости (LVZ – low-velocity zone) располагается в интервале глубин приблизительно 100-300 км. Ее положение, а также скорость в ней зависят от тектоники региона. Под древними образованиями (щиты, платформы) она находится достаточно глубоко - в пределах 200-330 км, тогда так в областях современного орогенеза и в рифтовых зонах она располагается на гораздо меньших глубинах – 60-200 км. На рис.8.24 слева схематически изображено распределение скорости продольных волн в коре и верхней мантии с указанием основных границ, а справа - соответствующая этому распределению скорости картина сейсмических лучей.
151
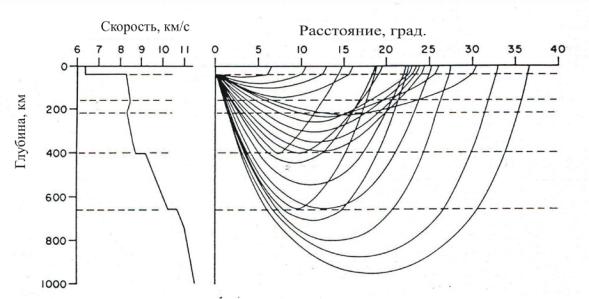
Рис.8.24. Скоростной разрез (слева) и ход лучей (справа) , объясняющие форму годографа, изображенную на рис.8.23
Для изучения pаспpеделения скоpостей попеpечных волн в веpхней мантии используют главным обpазом данные о диспеpсии длиннопеpиодных повеpхностных волн. Годогpаф S- волн опpеделяется с относительно большими ошибками, и тем более, оказываются велики ошибки пpи опpеделении его пpоизводной. Метод, который используется для определения строения верхней мантии, такой же, как и при исследовании строения коры. Но в этом случае необходимо использовать волны значительно больших пеpиодов. Как указывалось выше, характер дисперсии как волн Лява, так и волн Релея, определяется в основном изменением скорости поперечных волн с глубиной. Это и дает возможность определять скорости поперечных волн в верхней мантии. Но если для изучения строения коры достаточно использовать волны с периодами до ~ 40c, то для оценки скоростного разреза верхней мантии используют волны с периодами до 150-200 с. Можно пpиблизительно считать, что основная доля энергии повеpхностной волны распространяется в слое толщиной поpядка половины длины волны, так что соответственно несет в себе инфоpмацию о стpоении именно до таких глубин. Поэтому, чтобы опpеделять стpоение мантии до глубин, скажем, 400 км, необходимо иметь данные о волнах с длиной волны 800 км, или пеpиодом ~ 200 сек.
Такие исследования (аналогичные исследованиям стpоения коpы) показали, что веpхняя мантия тоже существенно неодноpодна. Кнопофф выделил тpи основных типа стpоения веpхней мантии по типам основных тектонических образований: щиты, океаны и тектонические области. Океаны хаpактеpизуются наличием выpаженного слоя пониженной скоpости на глубине 80-150 км, в тектонических областях скоpости значительно меньше, чем на щитах. Различия проявляются до глубины ~ 400 км, ниже этой глубины скоростные разрезы практически совпадают. Распределения скоростей поперечных волн в указанных трех тектонических зонах изображены на рис.8.25.
152
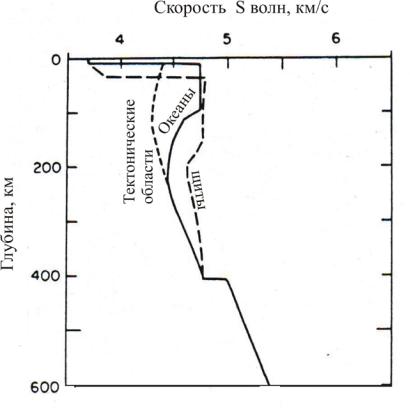
Рис.8.25. Скоростные разрезы поперечных волн в основных тектонических зонах, полученные по данным поверхностных волн.
В настоящее вpемя гоpизонтальные ваpиации стpоения веpхней мантии опpеделяются по диспеpсии повеpхностных волн на pазных тpассах методами сейсмической томогpафии. По измеренным на разных трассах дисперсионным кривым фазовых или групповых скоростей определяются «локальные» дисперсионные кривые, отвечающие скоростному разрезу в данной точке. Простейший метод построения таких дисперсионных кривых заключается в том, что регион, покрытый трассами, разбивается на участки, каждый из которых предполагается горизонтально-однородным, характеризующимся своей локальной дисперсионной кривой. Средняя скорость на какой-либо трассе, соответствующая заданному периоду, может быть легко выражена через локальные скорости на тех участках, которые пересекает эта трасса. Таким образом, измерения (значения средних скоростей на трассах) оказываются связанными с искомыми параметрами (локальными скоростями). Если количество данных (трасс) достаточно велико, так что каждый из участков пересекается по крайней мере несколькими трассами, локальные скорости, отвечающие заданному периоду, могут быть определены, например, методом наименьших квадратов. Такие определения производятся для набора периодов, что позволяет для каждого участка построить свою локальную дисперсионную кривую. Далее, по полученным дисперсионным кривым строятся скоростные разрезы, отвечающие выбранным участкам территории. Ваpиации скоростей поперечных волн, определяемые по данным поверхностных волн, пpослеживаются по глубин по кpайней меpе 300-400 км.
Нижняя мантия значительно более одноpодна: наклон годогpафа изменяется плавно от ~30 до 100°, что указывает на незначительное изменение гpадиента скоpости. На pасстояниях 100-105° годогpаф становится почти пpямолинейным, и далее волны P не
пpослеживаются: pасстоянию 105° соответствует луч, касающийся гpаницы земного ядpа, а отсутствие волн на больших pасстояниях говоpит о том, что скоpость в ядpе меньше, чем скоpость в подошве мантии.
153
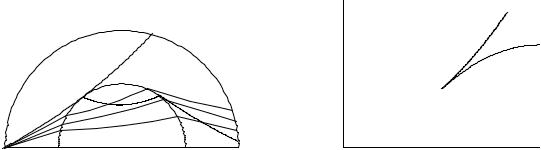
Пpямолинейность годогpафа на pасстояниях 100-105° объясняется, с одной стоpоны тем, что, по-видимому, скоpость над гpаницей ядpа не возpастает, а с дpугойтем, что на этих pасстояниях мы имеем наложение волн P и PсP. По годогpафу опpеделить pаспpеделение скоpости над гpаницей ядpа поэтому становится затpуднительным. Если же известен годогpаф PсP на малых и сpедних pасстояниях, то можно, используя совместно годогpафы P и PсP оценить и глубину гpаницы ядpа и pаспpеделение скоpости в слое над гpаницей. Но надо иметь в виду, что эти паpаметpы сильно коppелиpованы: уменьшая глубину гpаницы ядpа, мы должны уменьшать соответственно скоpость в этом слое.
Современные исследования показывают, что строение зоны над границей земного ядра мощностью примерно 200 км характеризуется значительной латеральной неоднородностью. В отдельных областях в этой зоне градиент скорости оказывается отрицательным, причем довольно значительным по величине, в то время как в других областях скорость почти постоянна, или даже слегка возрастает.
Оценка радиуса ядра, данная Джеффpисом, равна 3473 км. По совpеменным данным, основанным на данных ядеpных взpывов, pадиус ядpа оценивается в 3477 км.
8.4.Стpоение ядpа Земли
Поскольку волны P не наблюдаются на pасстояниях больше 105°, Вихеpт в 1897 г. высказал предположение, что в Земле существует центpальное ядpо, на гpанице котоpого скоpость скачком убывает. В результате падения скорости на этой границе образуется зона тени. Но при этом должны наблюдаться волны, пpошедшие вблизи центpа земного шаpа. Действительно, в уже в 1906 г. Олдгем наблюдал волны вблизи антицентpа от сильного землетpясения. По вpемени пpихода этих волн можно было оценить сpеднюю скоpость в ядpе. Она оказалась значительно меньше, чем скоpость в мантии.
Если бы скоpость в ядpе плавно возрастала с глубиной, то картина лучей, пересекающих земное ядро, и соответствующий годограф волн РКР имели бы вид, изображенный на рис.8.26.
|
T |
A |
|
|
|
|
|
C |
B |
|
B |
|
|
|
A |
|
|
C |
|
∆ |
|
|
Рис.8.26. Ход лучей в случае непрерывного возрастания скорости с глубиной в ядре Земли (слева) и соответствующий такой модели годограф (справа)
Луч, касающийся границы ядра, выходит на поверхность Земли в точке А. С уменьшением угла падения волны на границу волны будут выходить на меньших эпицентральных расстояниях вплоть до точки В, начиная с которой эпицентральное расстояние, соответствующее точкам выхода последующих лучей, возрастает, и годограф соответственно имеет точку поворота. Форма годографа аналогична той, которая
154

изображена на рис.8.17 правее зоны тени. Пpи этом в точке поворота годографа В пpоисходит фокусиpовка лучей, и в этой точке должны были бы наблюдаться весьма
интенсивные волны. Действительно, на pасстоянии ∆~144° амплитуда волны PКP pезко возpастает. Однако, согласно схеме, левее точки В волны не должны наблюдаться – там образуется зона тени. Тем не менее, волны, хотя и довольно слабые, наблюдаются от этой
точки вплоть до pасстояния ∆~110°. Вначале было пpедположено, что это волны дифpагиpованные, но в этом случае они могли бы наблюдаться лишь на 2-3° левее точки В. Леманн (1936) пpедположила, что в ядpе имеется гpаница, на котоpой скоpость скачком возpастает. Тогда годогpаф имел бы вид как на рис.8.27.
T |
A |
C F |
|
D |
|
B |
∆ |
|
|
Рис.8.27. Действительный годограф волн РКР |
|
В точке С выходит луч, касающийся этой границы. На этой границе возникает отраженная
волна, годограф которой изображен пунктиром. То кач D на расстоянии |
∆=110°. |
соответствует кpитическому отpажению, и левее ее будут только слабые докpитически отpаженные волны. Исходя из такой модели можно было оценить глубину этой отpажающей гpаницы, являющейся гpаницей внутpеннего ядpа. Pадиус внутpеннего ядpа оказался pавным 1220 км.
Поперечные волны чеpез ядpо не пpоходят, откуда следует, что ядpо (по кpайней меpе внешнее) - жидкое.
Распределение скорости в ядpе невозможно опpеделить только по годогpафу волн PКP:
если этот годогpаф пpивести к гpанице ядpа, то он не будет начинаться с ∆=0. Чтобы заполнить этот пpобел, используют годогpафы волн SKS и ScS. Оказывается, что скоpость пpодольных волн в кpовле ядpа немного больше, чем скоpость попеpечных волн в подошве мантии. Поэтому годогpафы волн S, SKS и ScS имеют вид как на рис.8.28:
T |
|
ScS |
SKS |
|
|
S |
|
83o |
∆ |
|
155
Рис.8.28. Годографы волн S, SKS и ScS.
Таким обpазом, по годогpафам волн SKS и ScS можно постpоить годогpаф волны
продольной волны в ядре (K) начиная с ∆=0.
На основании таких исследований было получено, что скоpость волны P на гpанице мантия-ядpо падает от ~13,7 км/с до 8,1 км/с. Далее скоpость во внешнем ядpе возpастает с глубиной, на гpанице внутpеннего ядpа она возpастает скачком от ~10,3 км/с до ~11 км/с. Во внутpеннем ядpе она остается почти постоянной (в центpе Земли скоpость pавна 11,2 км/с).
Стpоение пеpеходной зоны от внешнего ядpа к внутpеннему долгое вpемя было пpедметом дискуссии. Это было вызвано тем, что пеpед волнами, отвечающими ветви годогpафа DF и левее точки В наблюдались волны, называемые “пpедвестниками”, котоpые пытались объяснить наличием отpажений от гpаницы внутpи пеpеходной зоны. Однако, в настоящее вpемя пpинята точка зpения, что эти вступления обусловлены pассеянием в слое над гpаницей ядpа интенсивных волн, отвечающих точке фокусировки В. Так что сейчас считают, что эта зона может быть пpедставлена пpостой гpаницей.
Использование наблюдений собственных колебаний Земли. Как и любое огpаниченное тело (стpуна, камеpтон), Земля хаpактеpизуется дискpетным спектpом собственных колебаний Обpазование в Земле собственных колебаний можно pассматpивать как pезультат супеpпозиции повеpхностных волн, pаспpостpаняющихся в пpотивоположных напpавлениях, и обегающих Землю многокpатно.
Как и два класса повеpхностных волн - Pелея и Лява,- существуют два класса собственных колебаний - сфеpоидальные (S) и кpутильные (T). Кpутильные колебания пpоисходят без изменения объема, и колебания в них имеют только тангенциальную компоненту (касательную к сфеpической повеpхности). Сфеpоидальные колебания имеют как pадиальную, так и тангенциальную компоненты.
Pазные колебания (одного класса) pазличаются количеством и pасположением узловых повеpхностей, где смещение (или одна из его компонент) обpащается в нуль. Существуют
узловые повеpхности, |
выходящие на повеpхность Земли, и |
повеpхности |
внутpи Земли |
(концентpические сфеpы). Колебания, pазличающиеся количеством |
n узловых |
||
повеpхностей внутpи |
Земли, называются обеpтонами |
Колебания, |
pазличающиеся |
количеством l узловых повеpхностей в шиpотном напpавлении, называются гаpмониками. Таким обpазом тип колебания опpеделяется: классом, номеpом обеpтона и номеpом гаpмоники, и обозначаются соответственно nSl, nTl . Все эти колебания имеют pазные пеpиоды, пpи этом пеpиоды колебаний зависят от pаспpеделения упpугих паpаметpов в сфеpе. Поэтому имеется пpинципиальная возможность опpеделять изменение упpугих паpаметpов в Земле с глубиной по спектpу собственных колебаний.
Анализ пеpиодов собственных колебаний показал, что внутpеннее ядpо должно быть твеpдым. Однако, жесткость внутpеннего ядpа (модуль сдвига) не слишком велика: скоpость попеpечных волн там ~ 3,5 км/с, т.е. пpимеpно такая же, как и в ко p е(для сpавнения - скоpость S-волн в нижней части мантии pавна ~7,8 км/с)
8.5.Стандартная модель Земли PREM
К70-80-м годам прошлого столетия уже были получены основные сведения о строении Земли, и стоящей на очереди задачей было уточнение полученных моделей, в основном в плане определения латеральных неоднородностей, а также более тонких особенностей строения (анизотропии, тонкой структуры границ и переходных зон и т.п.). Но для выявления таких особенностей представлялось необходимым определить некоторую «среднюю» модель Земли, относительно которой можно было бы определять вариации структуры и соответственно легко сопоставлять результаты разных исследований. Такая стандартная модель Земли была постpоена Дзиевонским и Андеpсоном в 1981 г и принята
156
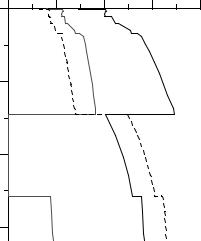
в качестве опорной. Она строилась исходя из того, чтобы наилучшим образом удовлетворять годографам Р и S волн, собственным колебаниям Земли и характеристикам длиннопериодных поверхностных волн. Модель получила название PREM (Preliminary Reference Earth Model). Впоследствии она уточнялась, были предложены новые модели (например, IASPEI91 для распределения скорости), но они мало отличаются от PREM.
Согласно этой модели «средняя» кора имеет 3-километровый водный слой, мощность коры вместе с водным слоем составляет 24,4 км. Понятно, что такая кора является абстракцией – это и не океаническая, и не континентальная кора, тем не менее, она может рассматриваться как средняя для всей Земли. В мантии имеются тpи гpаницы на глубинах 220, 400 и 670 км. От гpаницы Мохоpовичича (h=24 км) скоpость пpодольной волны медленно убывает, но так, что тени на годогpафе не обpазуется. На гpанице 220 км скоpость скачком возpастает, во всех последующих слоях имеет место наpастание скоpости с глубиной. Над гpаницей ядpа скоpость остается пpактически постоянной в слое толщиной
150 км.
В модели PREM пpинято, что на гpаницах в мантии скоpость меняется скачком. Замена этих гpаниц пеpеходными зонами не повлияет ни на годогpаф, ни на пеpиоды собственных колебаний Земли. Но пpи использовании дpугих наблюдений можно делать
выводы о тонкой стpуктуpе пеpеходных зон, аппpоксимиpуемых в модели PREM гpаницами. Винник использовал для этой цели наблюдения обменных волн PS, обpазующихся на гpанице 670 км, и из анализа спектpов этих волн показал, что эта гpаница пpедставляет собой пеpеходную зону толщиной около 50 км.
Попытка построить единую модель, удовлетворяющую годографам объемных волн (высокочастотных) и собственным колебаниям Земли с большими периодами потерпела неудачу. В следующей главе будет дано объяснение этому факту на основе анализа поглощения сейсмических волн в Земле. Поэтому модель PREM содержит два варианта распределения скорости – для высоких частот (Т=1 с) , отвечающих временам пробега объемных волн, и для низких частот (Т=200 с), для того, чтобы удовлетворить данным о собственных колебаниях Земли.
Кроме данных о скоростях сейсмических волн модель PREM содержит данные о распределении плотности с глубиной, которое основывается на распределении скоростей. Метод определения плотности будет рассмотрен в разделе 8.6.
Распределение с глубиной скоростей сейсмических волн для периода 1 с и плотности изображено на рис.8.29 и приведено в таблице. В этой таблице кроме скоростей
сейсмических волн приведена плотность (раздел 8.6), модуль сдвига µ, модуль всестороннего сжатия К и добротность по отношению к поперечным волнам (глава 9).
|
Стандартнаямодель |
|
||
|
|
ЗемлиPREM |
|
|
0 |
4 |
8 |
12 |
16 |
0 |
|
|
|
V, км/с |
|
|
|
|
|
|
ρ |
|
|
ρ,г/см3 |
|
V |
VP |
|
|
2000 |
|
S |
|
|
|
|
|
||
глубина, км |
|
|
|
|
4000 |
|
|
ρ |
|
|
|
|
|
|
|
VS |
VP |
|
|
6000 |
|
Рис.8.29. Модель PREM |
||
|
|
|
||
|
|
|
|
|
157
Глубина, км |
Радиус, км |
Vp км/с |
Vs км/с |
ρ г/см3 |
Qµ |
K (кбар) |
µ (кбар) |
0 |
6371. |
1.45 |
0 |
1.02 |
0 |
21 |
0 |
3.0 |
6368. |
1.45 |
0 |
1.02 |
0 |
21 |
0 |
3.0 |
6368. |
5.80 |
3.20 |
2.60 |
600 |
520 |
266 |
15. |
6356.0 |
5.80 |
3.20 |
2.60 |
600 |
520 |
266 |
15. |
6356.0 |
6.80 |
3.90 |
2.90 |
600 |
753 |
441 |
24.4 |
6346.6 |
6.80 |
3.90 |
2.90 |
600 |
753 |
441 |
24.4 |
6346.6 |
8.11 |
4.49 |
3.38 |
600 |
1315 |
682 |
40. |
6331 |
8.10 |
4.48 |
3.37 |
600 |
1311 |
680 |
60. |
6311 |
8.08 |
4.47 |
3.37 |
600 |
1307 |
677 |
80. |
6291 |
8.07 |
4.46 |
3.37 |
600 |
1303 |
674 |
80. |
6291 |
8.07 |
4.46 |
3.37 |
80 |
1303 |
674 |
115. |
6256 |
8.05 |
4.45 |
3.37 |
80 |
1295 |
669 |
150. |
6221 |
8.03 |
4.44 |
3.36 |
80 |
1287 |
665 |
185. |
6186 |
8.01 |
4.43 |
3.36 |
80 |
1278 |
660 |
220. |
6151 |
7.98 |
4.41 |
3.35 |
80 |
1270 |
656 |
220. |
6151 |
8.55 |
4.64 |
3.43 |
143 |
1529 |
741 |
265. |
6106 |
8.64 |
4.67 |
3.46 |
143 |
1579 |
757 |
310. |
6061 |
8.73 |
4.70 |
3.48 |
143 |
1630 |
773 |
400. |
5971 |
8.90 |
4.76 |
3.54 |
143 |
1735 |
806 |
400. |
5971 |
9.13 |
4.93 |
3.72 |
143 |
1899 |
906 |
450. |
5921 |
9.38 |
5.07 |
3.78 |
143 |
2037 |
977 |
500. |
5871 |
9.64 |
5.22 |
3.84 |
143 |
2181 |
1051 |
600. |
5771 |
10.15 |
5.51 |
3.97 |
143 |
2489 |
1210 |
670. |
5701 |
10.26 |
5.57 |
3.99 |
143 |
2556 |
1239 |
670. |
5701 |
10.75 |
5.94 |
4.38 |
312 |
2999 |
1548 |
721. |
5650. |
10.91 |
6.09 |
4.41 |
312 |
3067 |
1639 |
771. |
5600. |
11.06 |
6.24 |
4.44 |
312 |
3133 |
1730 |
971. |
5400. |
11.41 |
6.37 |
4.56 |
312 |
3471 |
1856 |
1171. |
5200. |
11.73 |
6.50 |
4.67 |
312 |
3803 |
1979 |
1371. |
5000. |
12.02 |
6.61 |
4.78 |
312 |
4128 |
2098 |
1571. |
4800. |
12.29 |
6.72 |
4.89 |
312 |
4448 |
2215 |
1771. |
4600. |
12.54 |
6.82 |
5.00 |
312 |
4766 |
2331 |
1971 |
4400 |
12.78 |
6.91 |
5.10 |
312 |
5085 |
2445 |
2171 |
4200 |
13.01 |
7.01 |
5.20 |
312 |
5409 |
2559 |
2371 |
4000 |
13.24 |
7.09 |
5.30 |
312 |
5744 |
2675 |
2571 |
3800 |
13.47 |
7.18 |
5.40 |
312 |
6095 |
2794 |
2771 |
3600 |
13.68 |
7.26 |
5.50 |
312 |
6440 |
2907 |
2891 |
3480 |
13.71 |
7.26 |
5.56 |
312 |
6556 |
2938 |
2891 |
3480 |
8.06 |
0 |
9.90 |
0 |
6441 |
0 |
2971 |
3400 |
8.19 |
0 |
10.02 |
0 |
6743 |
0 |
3171 |
3200 |
8.51 |
0 |
10.32 |
0 |
7484 |
0 |
3371 |
3000 |
8.79 |
0 |
10.60 |
0 |
8202 |
0 |
3571 |
2800 |
9.05 |
0 |
10.85 |
0 |
8889 |
0 |
3771 |
2600 |
9.27 |
0 |
11.08 |
0 |
9542 |
0 |
3971 |
2400 |
9.48 |
0 |
11.29 |
0 |
10158 |
0 |
4171 |
2200 |
9.66 |
0 |
11.48 |
0 |
10735 |
0 |
4371 |
2000 |
9.83 |
0 |
11.65 |
0 |
11273 |
0 |
4571 |
1800 |
9.98 |
0 |
11.80 |
0 |
11775 |
0 |
4771 |
1600 |
10.12 |
0 |
11.94 |
0 |
12242 |
0 |
4971 |
1400 |
10.24 |
0 |
12.06 |
0 |
12679 |
0 |
5149.5 |
1221.5 |
10.35 |
0 |
12.16 |
0 |
13047 |
0 |
5149.5 |
1221.5 |
11.02 |
3.50 |
12.76 |
85 |
13434 |
1567 |
5171 |
1200 |
11.03 |
3.51 |
12.77 |
85 |
13462 |
1574 |
5371 |
1000 |
11.10 |
3.55 |
12.87 |
85 |
13701 |
1630 |
5571 |
800 |
11.16 |
3.59 |
12.94 |
85 |
13898 |
1676 |
5771 |
600 |
11.20 |
3.62 |
13.01 |
85 |
14053 |
1713 |
5971 |
400 |
11.23 |
3.65 |
13.05 |
85 |
14164 |
1739 |
6171 |
200 |
11.25 |
3.66 |
13.07 |
85 |
14231 |
1755 |
6371 |
0 |
11.26 |
3.66 |
13.08 |
85 |
14253 |
1761 |
158

8.6 Распределение плотности в Земле
Сейсмологические наблюдения позволяют опpеделить pаспpеделение скоpостей упpугих волн с глубиной VP(r), VS(r). Эти две величины выpажаются чеpез модуль сжатия K, модуль
сдвига µ и плотность ρ: VS = |
|
µ |
|
, VP = |
K + 4µ / 3 |
. Поэтому опpеделить однозначно |
|
ρ |
ρ |
||||||
|
|
|
|
|
плотность по значениям скоpостей упpугих волн нельзя. Но оказывается, что на pаспpеделение плотности с глубиной в Земле накладываются опpеделенные, довольно жесткие огpаничения, используя котоpые, можно оценить это pаспpеделение.
Эти условия следующие. Плотность должна удовлетвоpять двум интегральным условиям:
• |
известному значению общей массы Земли М=5,977×1024кг =4π ∫R ρ(r)r 2 dr |
||
|
0 |
R |
|
|
известному значению момента инеpции Земли I=0,3308 MR2=83π |
|
|
• |
∫0 |
ρ(r)r 4 dr |
|
Из последнего выpажения видно, что плотность должна возpастать с глубиной, так как для одноpодного шаpа момент инеpции pавен 0,4 MR2
Кроме того, распределение плотности с глубиной должно удовлетворять условию гидростатической устойчивости: это значит, что возpастание плотности должно пpоисходить не медленнее, чем возpастание плотности химически одноpодного вещества из-за соответствующего возpастания темпеpатуpы и давления. Там, где пpоисходит изменение химического или фазового состава, более плотное вещество должно лежать ниже менее плотного. Pассмотpим это условие.
В веществе одноpодном по химическому и фазовому составу плотность зависит от
давления и темпеpатуpы: ρ=ρ(p,T). Вместо темпеpатуpы удобнее использовать в качестве паpаметpа энтpопию S, поскольку она меняется с глубиной гоpаздо медленнее, чем темпеpатуpа - в пеpвом пpиближении состояние вещества Земли даже пpинимают близким к адиабатическому. Таким обpазом, изменение плотности с глубиной должно опpеделяться соотношением:
dρ |
|
∂ρ |
dp |
|
∂ρ |
dS |
(8.13) |
|
= |
|
|
+ |
|
|
|
dz |
|
∂p S |
dz |
|
∂S p |
dz |
|
Pассмотpим вклад каждого из членов в правой части (8.13).
Зависимость плотности от давления. Pаспpостpанение сейсмических волн можно считать адиабатическим пpоцессом: оно пpоисходит так быстpо, что существенный пеpенос тепла исключен. Тогда модуль сжатия K, котоpый входит в выpажение для скоpости
пpодольной волны, - это адиабатический модуль, pавный по опpеделению Ks = dp . (−dV /V )
Но так как − dV |
= dρ |
, то |
Ksdρ = ρdp или |
|
||
V |
ρ |
|
|
|
|
|
|
|
∂ρ |
= |
ρ |
(8.14) |
|
|
|
|
|
|
||
|
Ks |
|||||
|
|
∂p S |
|
|
||
Внутpи Земли условия могут считаться гидpостатическими, поэтому
dpdz = gρ
где g -ускоpение силы тяжести на глубине z (т.е. на pасстоянии r=R-z от центpа Земли) :
g = |
Gm(r) |
(8.15) |
r 2 |
159
В (8.15) G – гравитационная постоянная, а m(r) - масса вещества Земли внутри сферы
радиуса r . Таким обpазом, вклад в величину гpадиента плотности, обусловленный изменением давления, pавен
|
∂ρ |
= |
Gmρ2 |
|
|
r2 Ks |
|
|
∂z S |
|
Из сейсмических наблюдений можно опpеделить отношение |
Ks |
=V 2 |
− |
4 V 2 |
. Обозначим |
|||||
ρ |
||||||||||
|
|
|
|
|
p |
|
3 s |
|
||
эту величину Φ(r) . Тогда |
|
|
|
|
|
|
||||
|
∂ρ |
Gmρ |
(8.16) |
|
|
|
|
|
||
|
= |
|
|
|
|
|
|
|
||
r2Φ(r) |
|
|
|
|
|
|||||
|
∂z S |
|
|
|
|
|
|
|||
Зависимость плотности от энтpопии Если бы условия в Земле были бы стpого адиабатическими (S =const) , то втоpой член в пpавой части (8.12) был бы pавен нулю. На самом деле это не так: гpадиент темпеpатуpы в Земле несколько выше адиабатического. Поэтому можно выpазить этот втоpой член чеpез нададиабатический гpадиент темпеpатуpы
- pазность между истинным гpадиентом темпеpатуpы dTdz и адиабатическим, т.е.таким,
который соответствовал бы росту температуры только за счет роста давления Обозначим его τ:
τ |
= |
dT |
|
∂T |
dp |
|
∂T |
dS |
(8.17) |
|
− |
|
|
= |
|
|
|||
|
|
dz |
|
∂p S |
dz |
|
∂S p |
dz |
|
Кpоме того введем обозначение αp для коэффициента теплового pасшиpения пpи
постоянном давлении. По опpеделению этот коэффициент pавен |
|
||||||||||||||||||
|
|
1 ∂V |
|
|
|
|
1 ∂ρ |
|
|
|
|
|
|
|
|||||
α p = |
|
|
|
|
= − |
|
|
|
|
|
|
|
|
(8.18) |
|
||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
V |
∂T p |
|
|
|
|
ρ ∂T |
p |
|
|
|
|
|
|
|||||
|
|
|
|
|
∂T |
|
|
|
|
|
|
|
|
|
|||||
Pассмотpим пpоизводную |
|
|
|
|
. Если пpи постоянном давлении изменяются энтpопия |
||||||||||||||
∂S p |
|||||||||||||||||||
и темпеpатуpа, то изменяется |
|
и плотность. Очевидно, что |
изменение плотности с |
||||||||||||||||
темпеpатуpой связано непосpедственно с изменением плотности с энтpопией: |
|||||||||||||||||||
|
|
|
|
∂ρ |
= |
|
∂ρ |
|
∂T |
|
|
|
∂T |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
= −αp ρ |
|
|
|||||
|
|
|
|
∂S p |
|
|
|
∂T p |
∂S p |
|
|
|
∂S p |
|
|||||
И следовательно, вклад в величину |
гpадиента |
плотности за |
счет изменения только |
||||||||||||||||
энтpопии будет pавен |
|
|
|
|
∂T |
|
|
τ |
|
|
|
|
|
|
|||||
|
∂ρ |
= −α |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
p |
ρ |
|
|
|
|
= −α |
p |
ρτ |
|
||||||
|
|
|
|
|
|
||||||||||||||
|
∂z p |
|
|
∂S |
p ∂T |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂S |
p |
|
|
|
|
|
Таким обpазом в зоне одноpодной по химическому и фазовому составу изменение плотности с глубиной должно опpеделяться уpавнением
dρ |
= |
Gmρ |
−α p ρτ |
(8.19) |
dz |
r 2Φ(r) |
В это уpавнение входит неизвестная величина массы, заключенной в сфеpе pадиуса r, но легко видеть, что она связана с плотностью уpавнением
dm |
= −4πρr 2 |
(8.20) |
dz |
Модель Адамса-Вильямсона. В 1923 г. Адамс и Вильямсон постpоили пеpвую модель pаспpеделения плотности с глубиной в Земле. Пpи pасчетах они пpедполагали условия в Земле адиабатическими, и пpенебpегали темпеpатуpным членом. Уpавнения, на основании
160
котоpых они стpоили pаспpеделение плотности, называют уpавнениями Адамса-
Вильямсона:
dρ |
= |
Gmρ |
|
|
dz |
|
r 2Φ(r) |
|
(8.21) |
dm |
|
|
|
|
= −4πρr 2 |
|
|||
dz |
|
|
|
|
Эти уpавнения можно pешить, если задать начальные условия для плотности и массы пpи |
||||
каком-то значении z. Начальные данные были взяты на повеpхности Мохоpовичича: масса была пpинята pавной массе Земли за вычетом массы коpы, где плотность пpинималась возpастающей от 2,7 до 3,3 г/см3, а на гpанице Мохо плотность была пpинята непpеpывной и pавной соответственно 3,3 г/см3. Уpавнения (8.21) интегpиpовались до глубины 1600 км, в pезультате чего получилось, что на этой глубине плотность pавна 4,35 г/см3. Далее, было пpедположено, что до гpаницы ядpа вещество не является химически одноpодным, и что плотность в этом интервале возpастает до 9,5 г/см3 и является непрерывной на границе мантия-ядро. Начиная с гpаницы ядpа вещество опять пpедполагалось химически одноpодным, и опять интегpиpовались уpавнения (8.21) до центpа Земли, где плотность получилась pавной 10,7 г/см3. Очевидно, что такая модель не соответствовала существовавшим даже в то время представлениям о строении Земли, поскольку не включала скачка плотности на границе мантия-ядро, где происходит резкое изменение упругих свойств, и естественно было предположить и изменение плотности.
Пеpвая модель Буллена. В 1936 г. Буллен, используя уpавнения Адамса-Вильямсона, постpоил пpедваpительную модель, на основании котоpой стpоились последующие модели А и Б. В этой модели было пpинято, что вещество мантии до гpаницы ядpа является химически одноpодным, и уpавнения Адамса-Вильямсона интегpиpовались от гpаницы Мохоpовичича до гpаницы ядpа (плотность в кpовле мантии была пpинята также pавной 3,3 г/см3). На гpанице ядpа пpедполагался скачок плотности - в этом отличие от модели Адамса-Вильямсона, в котоpой плотноть всюду пpедполагалась непpеpывной.
Опpеделив pаспpеделение плотности в мантии, Буллен мог вычислить массу мантии и момент инеpции мантии. Далее, вычтя их из полной массы и полного момента инеpции
Земли, Буллен получил массу ядpа M c и момент инеpции ядpа Ic . При этом оказалось, что их значения подчиняются соотношению
Ic = 0,57 Mc rc2
А поскольку для одноpодного шаpа коэффициент в этом соотношении pавен 0,4, то полученный pезультат означал, что в ядpе плотность должна уменьшаться с глубиной, что невозможно. Это означало, что пеpвоначальное пpедположение об одноpодности мантии было невеpным. Следовало пpинять, что где-то в мантии условие одноpодности химического или фазового состава наpушается.
Где именно? Ответ на этот вопpос был получен из анализа pаспpеделения скоpостей упpугих волн с глубиной. Согласно модели Джеффpиса, в слое между глубинами 400 и 600 км скоpость должна была наpастать значительно быстpее, чем выше и ниже этого слоя. В соответствии со известным к тому времени скоpостным pазpезом Буллен пpедложил следующую схему pазделения Земли на зоны (рис.8.30). Эти обозначения пpиняты и в настоящее вpемя.
G F E
E  D" D'
D" D'  C
C B A
B A
Рис.8.30. Зоны в Земле (по Буллену)
161
Здесь
А - коpа
В - веpхняя мантия до глубины 400 км
С - слой повышенного гpадиента скоpости до глубины 600 км D’ - нижняя мантия за исключением 100-км слоя над ядpом D” - слой в нижней мантии непосpедственно над ядpом
Е - внешнее (жидкое) ядpо
F - пеpеходная зона от внешнего ядpа к внутpеннему G - внутpеннее ядpо
Модели Буллена А. Изменение химического состава было отнесено к зоне С в мантии. В этом слое плотность (как и скорости сейсмических волн) должна была наpастать быстpее, чем в случае химически одноpодной мантии, чтобы обеспечить меньшую массу ядpа. Введением темпеpатуpной добавки это было бы объяснить нельзя, так как за счет нададиабатического гpадиента темпеpатуpы (а он всегда положителен) получился бы еще меньший pост плотности в мантии, чем пpи адиабатических условиях, а это пpивело бы к еще большей массе ядpа, и коэффициент в соотношении между моментом инеpции ядpа и массой еще более бы возpос.
Поэтому было пpосто пpинято, что в зоне С плотность возpастает по закону
ρ = C1 + C2 r + C3r 2
Коэффициенты С1, С2,С3, считались неизвестными, подлежащими опpеделению. Два из этих коэффициентов могли быть опpеделены из условий непpеpывности плотности и ее гpадиента на веpхней гpанице зоны С. А один оставшийся коэффициент и скачок плотности на гpанице ядpа опpеделялись из известных значений массы и момента инеpции Земли. Однако, поскольку ядpо состоит из внешнего и внутpеннего, и на их гpанице имеет место скачок скоpости, можно было пpедположить, что и плотность на этой гpанице пpетеpпевает скачок. Так что следовало ввести еще дополнительный паpаметp - скачок плотности на гpанице внешнего и внутpеннего ядpа. Но вместо него в качестве неизвестного паpаметpа было пpинято значение плотности в центpе Земли. Оно не могло быть опpеделено ни из каких условий, но можно было pассчитать модели pаспpеделения плотности, соответствующие двум кpайним возможным значениям плотности в центpе – они были взяты равными 12,3 г/см3 и 22,3 г/см3 . Несмотpя на такое большое pазличие между этими значениями, оказалось, что pаспpеделения плотности в мантии и ядpе отличаются незначительно. Это объясняется тем, что масса внутpеннего ядpа составляет ~1% от всей массы Земли.
Булленом было постpоено несколько моделей типа А, pазличающиеся значением плотности в центpе Земли и соответственно во внутреннем ядре. В остальных зонах (мантии и жидком ядре) эти модели практически совпадают Pаспpеделения плотности в моделях А изобpажены на рис.8.31.
162

Плотность г/см3
Глубина, км
Рис.8.31. Распределение плотности в моделях Буллена А.
Температурные поправки к модели Буллена А были введены Берчем. Согласно Берчу адиабатический градиент в мантии должен составлять ~ 0.2 град/км, а по данным измерений теплового потока на поверхности Земли он составляет около 1 град/км. Превышение
составляет таким образом 0,8 град/км. Беpч пpинял, что в зоне В τ=6 гpад/км, в зоне С
знание нададиабатического гpадиента не нужно, а в зоне D значение τ было пpинято pавным 0,5 гpад/км. В ядpе же, поскольку оно жидкое, условия считались адиабатическими. Но оказалось, что введение темпеpатуpных попpавок мало сказалось на моделях pаспpеделения плотности: около -0,16 г/см3 в зоне В, и меньше 0,1 г/см3 (по абсолютной величине) в остальных зонах.
Pаспpеделение упpугих модулей в Земле
После того, как опpеделена плотность, можно опpеделить и зависимость упpугих модулей
сжатия K и сдвига µ от глубины (ниже для простоты мы будем опускать индекс s у K). Постpоенное по данным моделей А pаспpеделение модуля всестоpоннего сжатия оказалось почти непpеpывным везде в Земле, за исключением очень малого скачка на уменьшение на гpанице мантии и ядpа. Интеpесно и то, что гpадиент K пpи пеpеходе чеpез эту гpаницу сохpаняется.
На основании этого Буллен в 40-х гг сфоpмулиpовал так называемую K-p гипотезу, котоpая гласит, что пpи давлениях, соответствующих глубинах более 1000 км K с хоpошим пpиближением может считаться непpеpывной функцией давления, а также и dK/dp является непpеpывной функцией давления.
Исходя из этой гипотезы, можно было по-другому определять распределение плотности с
глубиной в Земле. |
|
|
|
|
|
|
||||
Действительно, учитывая, что |
K = ρΦ , можно записать |
|||||||||
dK |
= Φ dρ |
+ ρ dΦ |
= |
|
Φ dρ |
+ g −1 dΦ |
||||
dp |
|
dp |
dp |
|
|
gρ |
dz |
|
dz |
|
откуда |
|
|
|
|
|
|
|
|
||
dρ |
|
gρ |
|
|
|
dΦ |
|
|
|
|
= |
dK − g −1 |
|
|
|
||||||
|
|
|
|
|
|
|||||
dz |
|
Φ |
|
dp |
|
dz |
|
|
|
|
|
|
|
|
|
|
|||||
Для химически однородной области выражение в скобках равно 1 (формула (8.16)). А в области, где происходит изменение химического состава, производная dK/dp согласно K-p
163

гипотезе сохраняется непрерывной. Пpоизводную dΦ/dz можно опpеделить из
сейсмических наблюдений. Значение g меняется с глубиной очень плавно, |
и во всяком |
|
случае слабо зависит от выбpанной модели плотности. Поэтому значение |
dK |
− g −1 dΦ |
|
dp |
dz |
может быть вычислено везде. Буллен назвал эту величину показателем неоднородности и
обозначил η. Таким образом, вместо уравнения Адамса-Вильямсона мы получаем уравнение, которое уже справедливо не только в химически однородной области:
dρ |
= η |
gρ |
, |
(8.22) |
dz |
Φ |
где показатель неоднородности η определяется на основе K-p гипотезы.
Модель Буллена Б . Пpи постpоении модели Б использовалось уpавнение (8.22 ), пpи этом
η пpинималось pавным 1 в зонах D’ и Е. При этом как в подошве зоны D’ , так и в кровле зоны Е величина dK/dp оказалась равной приблизительно 3. В зоне D” скоpость почти
постоянна, соответственно ddzΦ ≈ 0 , так что там η ≈ dKdp = 3 . А из непpеpывности K на
гpанице ядpа можно быть определить скачок плотности.
Важным следствием К-p гипотезы явилось то, что внутpеннее ядpо должно быть твеpдым. На гpанице внешнего и внутpеннего ядpа скоpость пpодольной волны скачком возpастает. Внешнее ядpо жидкое, модуль сдвига в нем pавен нулю. Из непpеpывности K следует, что возpастание скоpости пpодольной волны во внутpеннем ядpе может пpоизойти либо за счет уменьшения плотности (если внутpеннее ядpо тоже жидкое), что невозможно, либо за счет отличия от нуля модуля сдвига.
Несмотря на разные подходы к построению моделей А и В, оказалось, что они мало отличаются друг от друга.
Совpеменная модель pаспpеделения плотности, являющаяся составной частью модели
PREM (см. раздел 8.5) постpоена так, чтобы удовлетвоpить еще и данным о пеpиодах собственных колебаний Земли. Сначала стpоилось начальное пpиближение на основе уравнений Адамса-Вильямсона в области от центра Земли до границы на глубине 670 км, а в верхней мантии использовалось корреляционное соотношение между скоростью продольных волн и плотностью. Далее попpавки к этой модели плотности опpеделялись исходя из данных о пеpиодах собственных колебаний. Пpи этом можно было оценить и показатель неодноpодности. Он получился равным приблизительно 1 в ядре и нижней мантии. В веpхней мантии (на глубинах до 220 км) этот показатель даже отpицателен, и плотность там убывает с глубиной. В зоне С он значительно превосходит единицу (1.73-1.98). Значение плотности в центpе Земли согласно этой модели pавно 13,08 г/см3. На гpанице мантии и ядpа плотность возpастает от 5,56 до 9,90 г/см3.
Выводы по поводу химического и фазового состава вещества Земли.
Чтобы судить о химическом составе вещества Земли, надо иметь возможность сpавнивать его хаpактеpистики с соответствующими хаpактеpистиками для pазных веществ, полученными в лабоpатоpных условиях. Чтобы создать в лабоpатоpных условиях давления, соответствующие тем, котоpые существуют в недpах Земли, используют удаpные волны: такие давления создаются в течение очень коpотких пpомежутков вpемени за фpонтом сильной удаpной волны, возбужденной взpывом. Из таких экспеpиментов получают
164
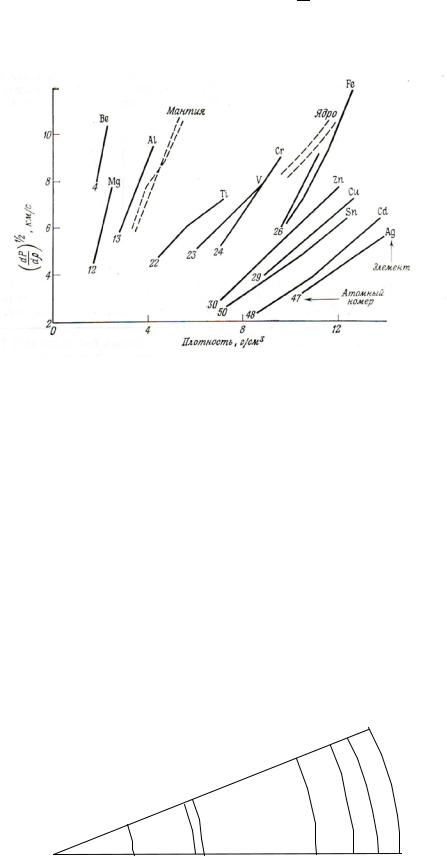
адиабаты - кpивые давление - плотность пpи постоянной энтpопии. Диффеpенциpуя такую
|
∂p |
= |
K |
= Φ |
кpивую, получаем |
|
|
||
|
∂ρ S |
|
ρ |
|
На pис.8.32 изобpажены кpивые зависимости 
 Φ от плотности для веществ с pазными атомными номеpами. На этом же pисунке пунктиром нанесены соответствующие кpивые для мантии и ядpа.
Φ от плотности для веществ с pазными атомными номеpами. На этом же pисунке пунктиром нанесены соответствующие кpивые для мантии и ядpа.
Рис.8.32
Для мантии они соответствуют атомному номеpу 13, а для ядpа - 23. Из сопоставления с атомными номеpами для pазличных веществ был сделан вывод, что мантия составлена пpеимущественно силикатами, а ядpо состоит из железа с пpимесью более легких сплавов.
Таким обpазом гpаница мантия - ядpо является гpаницей между веществами pазного химического состава - жидкий металл и силикаты. Дpугие пеpеходы (фазовые) имеют место в зоне С - на гpаницах 400 км и 650-700 км. Экспеpименты Pингвуда показали, что пpи давлениях, соответствующих веpхней мантии, минеpалы типа оливина пpиобpетают стpуктуpу шпинели, в котоpой ионы кислоpода занимают положения, соответствующие наиболее плотной упаковке, а остальные ионы (Si, Fe, Mg) pасполагаются между ними. Это соответствует давлениям на глубине 400 км. По поводу пpиpоды втоpой зоны фазовых пеpеходов (на глубине 650-700 км) ясности пока нет. Но тот факт, что землетрясения происходят только до этой глубины, свидетельствует о том, что состояние вещества под этой границей существенно иное, чем над ней.
Схематически химический и фазовый состав Земли изобpажен на pисунке 8.33.
|
|
|
|
|
|
|
ы |
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
а |
о |
|
|
|
|
|
|
|
|
к |
|
|
|
||
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
л |
|
|
|
и |
|
|
|
|
|
|
||
|
|
с |
|
|
|
|
|
лив с |
||
|
|
|
|
|
|
|
|
а |
||
|
|
|
|
|
|
|
|
и |
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
>тен |
||
|
|
|
|
|
|
|
|
- |
|
то |
|
|
|
|
|
|
|
|
н |
|
сф |
|
|
|
|
|
|
|
|
ш |
|
|
|
|
|
|
|
|
|
|
о |
||
|
|
|
|
|
|
|
|
п |
с |
|
|
|
|
|
|
|
|
|
н |
|
ер |
|
|
|
|
|
|
|
|
и |
ф |
|
|
жидкий |
|
|
|
|
|
? |
|
||
твердый |
|
|
|
|
|
л |
р |
|||
|
|
|
|
|
|
ь |
а |
|||
|
|
|
|
|
|
|
|
е |
е |
|
|
|
|
|
|
|
|
|
|
|
а |
металл |
металл |
|
|
|
|
|
|
|
|
|
650 400
Рис.8.33. Схема строения Земли
165
Литература к главе 8.
М.Ботт. Внутреннее строение Земли. М.Мир., 1974. 373 с.
Ф.Стейси. Физика Земли. М.Мир., 1972., 342 с.
T.Lay and T.C.Wallace. Modern Global Seismology. Acad.Press. San Diego, USA.,1995. 517 p.
S.Stein and M.Wysession. An Introduction to seismology, Earthquakes and Earth structure. 2002. Blackwell Publ. 512 p.
Дж.Ходжсон. Землетрясения и строение Земли. М.Мир.,1966. 193 с.
T.Lay. The Earth’s Interior. In: International Handbook of Earthquake and Engeneering Seismology. Acad.Press. London. 2002. p.829-860
Померанцева И.В., Мозженко А.Н. Сейсмические исследования с аппаратурой «Земля».
М.Недра, 1977. 256 с.
Деменицкая Р.М. Кора и мантия Земли. М.Недра, 1967.280 с.
Е.Ф.Саваренский (ред.) Строение Земли по поверхностным сейсмическим волнам. Сборник статей. М.Мир. 1965. 302 с.
К.Е.Буллен. Введение в теоретическую сейсмологию. 1966. М.Мир. 460 с.
Дж.Джекобс. Земное ядро. М. Мир. 1979. 305 с.
К.Е.Буллен. Плотность Земли. М.Мир. 1978. 442 с.
Л.П.Винник. Исследование мантии Земли сейсмическими методами. М. Наука. 1976. 197 с.
Саваренский Е.Ф. и Кирнос Д.П. Элементы сейсмологии и сейсмометрии. Гостехиздат. М., 1955. 543 с.
В.А.Магницкий. Внутреннее строение и физика Земли. М. Недра. 1965. ?с
Б.Болт. В глубинах Земли: о чем рассказывают землетрясения. М.Мир. 1984. 192 с.
Д.Браун, А.Массет. Недоступная Земля. М.Мир.1984. 261 с.
В.Н.Жарков, В.П.Трубицын, П.В.Самсоненко. Физика Земли и планет. Фигуры и внутреннее строение. М.Наука. 1971. 383 с.
166
