Движение, описываемое скалярным потенциалом ϕ, представляет волну,

распространяющуюся со скоростью a = λ +ρ2µ , а движение, описываемое векторным потенциалом Ψ - волну, распространяющуюся со скоростью

b = µρ . Чтобы решить эти уравнения, мы должны знать начальные условия,

т.е. функции ϕ(x) и ψ(x) в момент t=0.

Решения уравнений (2.24) являются аддитивными, т.е. если ϕ1 и ϕ2 два различных решения волнового уравнения, то ϕ1 +ϕ2 также будет решением.

Это значит, что путем суперпозиции различных (элементарных) решений мы можем построить такое, которое удовлетворяет заданным начальным условиям. Простейшим элементарным решением волнового уравнения является решение в виде плоской волны.

2.7. Плоские волны

Рассмотрим вначале скалярное волновое уравнение

u = u(x,t)

Решение уравнения (2.25) может быть представлено в следующем общем виде:

собой волну, распространяющуюся в направлении вектора k со скоростью с. Направление вектора k является произвольным. Очевидно, что в любой момент времени t на плоскости (k,x)=const значение функции u будет одним и тем же.

Запишем теперь решения уравнений (2.24) в виде плоских волн:

где l – некоторый единичный вектор, имеющий произвольное направление. Тогда выражение для смещения, являющего решением уравнения движения упругой среды, может быть записано в виде

u = uP + uS

Первое слагаемое описывает волну, в которой смещение происходит в направлении вектора kP, т.е. в направлении распространения волны. Такая волна называется продольной и обозначается P. Волна, описываемая вторым слагаемым, распространяется в направлении вектора kS, а смещение в ней

30

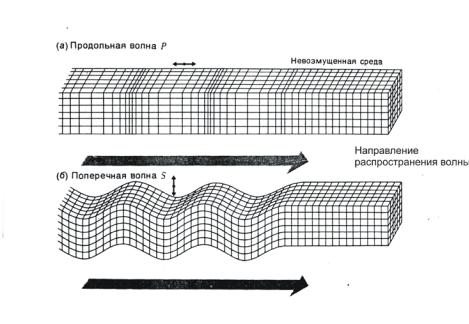
происходит перпендикулярно направлению распространения. Такая волна называется поперечной (S). Скорость продольной волны всегда больше скорости поперечной. Характер движения в плоских продольной и поперечной волнах изображен на рис.2.6.

Рис.2.6. Движение в продольной и поперечной волнах

Решение уравнения движения в виде плоской волны можно построить, не прибегая к выражению смещений через потенциалы. Из (2.27) видно, что смещение как в продольной, так и в поперечной волне можно представить в общем виде следующим образом:

где n и l – некоторые единичные вектора, а c – скорость распространения волны. Вектор n определяет направление распространения волны, а вектор l – направление смещения в волне, или ее поляризацию. Используя концепцию плоских волн, мы покажем, что скорость c может быть равна a или b, при этом

Действительно, подставляя представление (2.28) в уравнение движения (2.18) (считая f=0) , мы получим

[(λ + µ)n(l,n) + µl]Φ′′(t − (n, x) / c)= ρc2lΦ′′(t − (n, x) / c)

или

31

Учитывая, что n единичный вектор, т.е. что nx2 + ny2 + nz2 =1, нетрудно показать,

что собственное значение удовлетворяет уравнению:

θ 3 −θ 2 = 0

Это уравнение имеет три корня:

θ1 =1, θ2 =θ3 = 0

Иначе

собственные векторы взаимно ортогональны, то векторы, соответствующие двум другим собственным значениям, ортогональны вектору n, т.е. направлению распространения волны, и в то же время они ортогональны между собой. Соответствующие этим корням волны распространяются с одной и той же скоростью b, но поляризованы в двух взаимно перпендикулярных направлениях. Равенство скоростей этих волн (поперечных) имеет место только в случае изотропной среды. В анизотропной среде все собственные значения оказываются различными. При этом поляризация продольной волны не совпадает с направлением распространения (поэтому такая волны называется квазипродольной), а две другие волны, поляризованные ортогонально квазипродольной волне, называются квазипоперечными, и их скорости не одинаковы.

2.8. Неоднородные плоские волны

При решении уравнения движения на основе представления (2.28) единственное предположение, которые мы делали относительно векторов l и n , было то, что эти векторы должны быть единичными, т.е.

(n,n)=1, (l,l)=1

При этом не обязательно, чтобы эти векторы были вещественными – они в общем могут быть и комплексными. Но если n является комплексным, то

аргумент функции Φ также будет комплексным, и соответственно сама функция Φ будет комплексной.

Итак, пусть n и l комплексные векторы

32

n = n1 + in2 l = l1 + il2

аргумент функции Φ является комплексным числом x+iy, и сама функция Φ также содержит вещественную и мнимую части:

Φ(x + iy) = f (x, y) + ig(x, y)

Поскольку n и l единичные векторы, мы будем иметь следующие соотношения для векторов n1 ,n2 ,l1 ,l2 :

(n1 ,n1 ) − (n2 ,n2 ) + 2i(n1 ,n2 ) =1

(n1 ,n1 ) − (n2 ,n2 ) =1 (n1 ,n2 ) = 0

(l1 ,l1 ) − (l2 ,l2 ) =1

(l1 ,l2 ) = 0

Смещение u должно быть вещественным, поэтому следует брать только вещественную часть комплексного решения:

Это выражение описывает неоднородную плоскую волну. Движение в такой волне можно представить следующим образом. Смещение ведет себя во времени одинаково вдоль прямых линий, определяемых пересечением плоскостей (x,n1)=const и (x,n2)=const. Волна распространяется в направлении

неоднородной волны всегда меньше c (т.е. a или b). Форма волны и ее амплитуда изменяются в направлении вектора n2. Компоненты смещения вдоль векторов l1 и l2 изменяются по-разному в соответствии с функциями f и g.

Векторы l1 и l2 в продольной волне совпадают с векторами n1 и n2. В поперечной волне векторы l1 и l2 удовлетворяют соотношениям

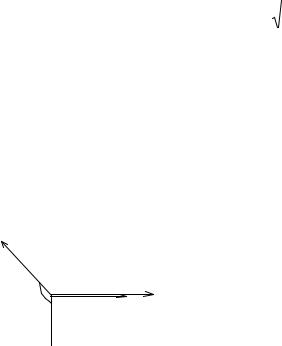
На рис.2.7 показана ориентация векторов n1 , n2 , l1 , l2 в волне S.

l1

n2

Рис.2.7. Ориентация вещественной и мнимой частей векторов n и l в поперечной волне.

33

Из (2.32) следует, что

cos β = − (n1 ,l2 ) n2 l1

Если β=π, то волна поляризована в плоскости векторов n1 , n2, так что она будет иметь продольную компоненту, т.е. в направлении распространения волны.

Такая волна называется волной SV. Случаю β=π/2 соответствует l2=0, при этом волна будет иметь только одну компоненту в направлении перпендикулярном плоскости векторов n1 , n2, т.е. она будет поляризована линейно. Такая волна называется волной SH.

Если движение в волне представляет собой гармонические колебания с круговой частотой ω, т.е. Φ(z) = Aexp(iωz) = Aexp(iωx −ωy) , то

f (x, y) = Ae−ωy cosωx

g(x, y) = Ae−ωy sinωx

Движение частиц в неоднородной гармонической волне будет эллиптическим в P и SV волнах и линейным в SH волне (рис.2.8)

Рис.2.8.

Движение частиц в волнах P. SV и SH.

В общем случае функции f(x,y), g(x,y) могут быть представлены в виде суперпозиции затухающих гармонических колебаний, т.е.

Так как время t входит только в вещественную часть аргумента функций f и g, т.е. в x = t − (n1 , x) / c , то форма волны в определенной точке x определяется

как функция этого аргумента. Из (2.33) видно, что функция g как функция x (или t) является преобразованием Гильберта функции f.

34