Гравитационное поле

Потенциал силы тяжести

Сила тяжести – равнодействующая силы притяжения Земли и центробежной силы, возникающей вследствие вращения Земли.

1. Сила притяжения: По закону Ньютона:

Рассмотрим прямоугольную систему координат с началом в центре масс Земли; ось Z направим по оси вращения, плоскость xy совместим с плоскостью экватора (пока – произвольно).

A – точка изучаемого тела

P – точка наблюдения с единичной пробной массой

Сила притяжения точки P телом в проекциях на оси X, Y, Z имеет вид:

2. Центробежная сила С

Она направлена перпендикулярно к оси вращения:

где r – расстояние до оси вращения.

В проекциях на оси X, Y, Z:

Учитывая, что пробная масса единичная, проекции силы тяжести перепишем как проекции ускорения:

И тогда потенциал силы тяжести имеет вид:

и наоборот: – сила тяжести в произвольном направлении s.

В системе XYZ:

Краткий анализ потенциала:

Свойства:

1. Потенциал W внутри Земли (даже в ее центре, т.е. при  имеет конечные значения. В частности:

2. Рассмотрим 2 частных случая:

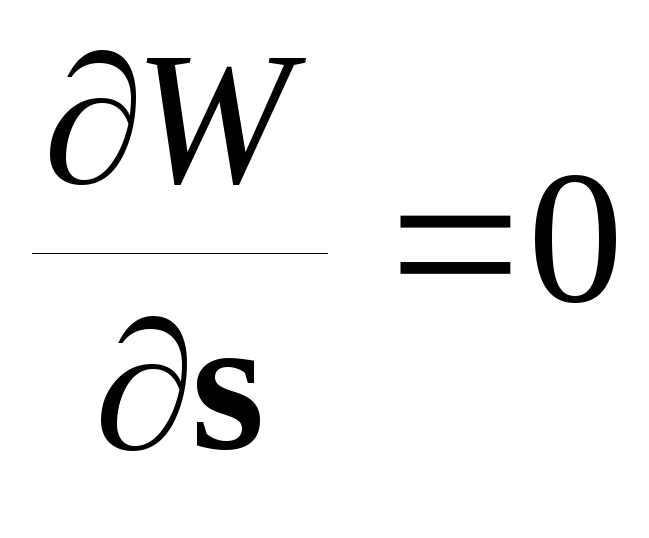1. Направление s перпендикулярно к g: . Тогда: и . Это – уравнение поверхности, на которой сила тяжести всюду нормальна к ней. Имеем уровенную поверхность. Одна из таких поверхностей (отвечающая некоторому конкретному значения константы: ), очевидно, совпадает с поверхностью невозмущенной (ветер, приливы) воды Мирового океана. Эту поверхность принимают за фигуру Земли и называют геоидом. Впрочем, сила тяжести на геоиде различна в разных местах (см. теорему Клеро).

2. Пусть угол . Тогда и , или . Это означает: если W – различие потенциалов двух уровенных поверхностей, а S – расстояние между ними, то это расстояние 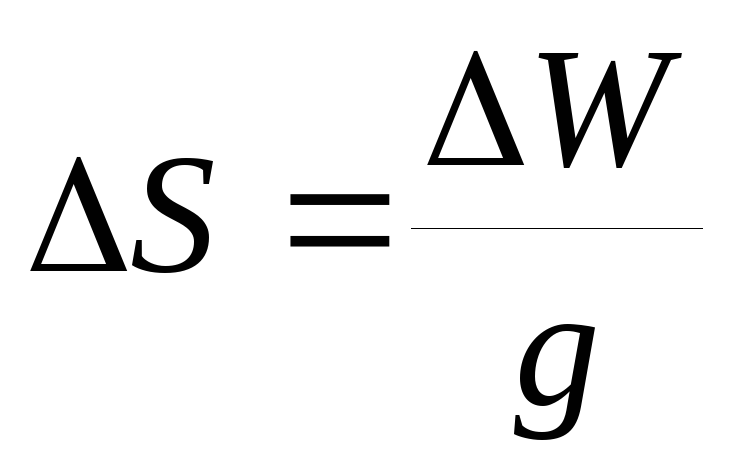будет разным в разных местах, в обратной зависимости от g.

Разложение потенциала тяготения в ряд

Потенциал силы тяжести:

.

Однако, так как ни форма, ни распределение масс «не заданы» для Земли, то выражение «неконструктивно". Разве что для однородного невращающегося шара на его поверхности: .

Однако, учитывая факт, что для Земли отклонение от шара невелико, W можно разложить в ряд с небольшим числом “значимых” членов. То же относится и к силе g и, значит, коэффициенты ряда могут быть определены из наблюдений.

Итак, разложим потенциал W в ряд:

Опять: () P(x, y, z) – точка наблюдения, () A(ξ, η, ζ ) – точка расположения элемента массы dm, r₁ и r – их радиус-векторы,  – угол между r₁ и r.

Тогда: ,

где .

Известно разложение:

Полиномы Лежандра:

.

Этот ряд сходится при и расходится при .

Тогда имеем (ограничившись приведенными членами разложения):

Проанализируем это выражение:

1. Первый член: – Потенциал шара.

2. Второй член:

Интегралы в этом выражении – это координаты центра масс тела:

Поместив, по соображениям симметрии, начало координат системы XYZ в этот центр масс, имеем: . Значит, второй член разложения равен нулю:

3. Третий член (опять подставляем cos :



Интегралы вида: в механике называются произведениями инерции.

С учетом высокой осевой симметричности Земли можем, направив оси XYZ по главным осям инерции, добиться их равенства нулю.

Третий член станет:

Введем моменты инерции относительно осей X, Y, Z:

,

а также, учитывая , получим:

Перейдем к сферическим координатам r, φ, λ (поворот осей X и Y, необходимый для обращения произведений инерции в ноль, изменит только долготу на величину ₀ ):

Принимаем ₀ = 0; в итоге, для третьего члена имеем:

И теперь, собственно потенциал силы тяжести, опустив значок возле r₁ (поскольку по r уже проинтегрировали), запишем: (первый + третий члены):

,

где . 1

Это выражение справедливо до малых второго порядка относительно сжатия , оно дает уже довольно конкретное (аналитическое) выражение для W.

Приравняв его: W = const – получим уравнения уровеннвх поверхностей. Одна из них (для const = const₀), с точностью до принятых упрощений, отвечает истинной форме Земли, являясь практически геоидом.

Найдем соответствующую const₀, – получим уравнение “дневной” уровенной поверхности. Подставим в 1 координаты одной из точек “реальной” поверхности Земли: φ = 0, λ = 0, r = a. Тогда:

2

Уравнение поверхности примет вид: 1 = 2.

Полученное равенство (ур-ие) можно записать в виде:

Обозначим:

их оценка: .

Учитывая порядок величин n, m, q относительно , принимая и , заменяя и отбрасывая q / 2 ~ , получим:

Так как Земля – тело, близкое к телу вращения, то , поэтому m ~ ² и может быть опущено. Тогда

3

А это есть уравнение сфероида: со сжатием . Значит, геоид близок к сфероиду, сжатие которого .

Начиная разложение потенциала в ряд, мы исходили, вообще говоря, из произвольной формы гравитирующего вращающегося тела. Однако далее, начав интерпретацию первых членов разложения, мы "незаметно для себя" стали ограничивать исходные свободы:

1. тело имеет конечную массу M;

2. поместили, как очевидное, центр системы в центр масс (попавший и на ось вращения), и тогда сразу стали говорить о высокой симметрии тела 

3.  а именно: произведения инерции равны 0, приняли: ₀ = 0;

4. моменты инерции: A = B;

5. , где  это говорит о том, что C тоже близок к A и B, т.е., в итоге, за основу-то в выводе мы взяли что-то типа шара. А уж шар, вращаясь, действительно дал сфероид.

Сила тяжести на поверхности идеальной Земли. Теорема Клеро.

Поверхность Земли (в идеале) – уровенная, поэтому сила тяжести нормальна к ней, т.е.:

.

Однако в наши выражения для W нормаль n не входит явно. Есть только r. Но для геоида они близки. Максимальное расхождение между ними на геоиде – на широте 45º и составляет . Значит, .

Возьмем W с точностью до :

.

Тогда:

.

Опять ; учитывая 3, получим:

.

Поскольку на экваторе, где  = 0:

,

то , 4

где .

На полюсах: , откуда – параметр сжатия.

Вспомним 3: – сжатие сфероида, поэтому:

5

Уравнения 4 и 5 составляют теорему Клеро.

Величина – до малых второго порядка есть отношение центробежной силы на экваторе к силе тяжести на экваторе.

В теореме Клеро равенство 5

дает, что сжатие  уменьшается при увеличении . Иными словами, чем сильнее возрастает сила тяжести с увеличением широты, тем меньше сжатие геоида (форма Земли должна быть ближе к сферической). Иначе говоря, чем ближе геоид к сфере, тем больше разность между силой тяжести на полюсах и экваторе. Говорят, что даже Ньютона это смущало.

Причина указанного, странного, на первый взгляд, обстоятельства состоит в том, что геоид может оставаться эквипотенциальной поверхностью только в том случае, если при изменении величины его сжатия происходит перераспределение масс внутри него самого. Так, в модели Ньютона ():

.

В модели Гюйгенса ():

,

откуда видно, что в этих моделях и меняются в противоположных направлениях.

Теорема Клеро, т.е. уравнение 4 дает приближенный закон распределения силы тяжести на геоиде – закон нормального распределения силы тяжести. Уравнение 5 позволяет определить сжатие Земли, зная значение g на двух разных широтах (в частности, на полюсах и экваторе).

Полное изменение силы тяжести от экватора к полюсу ~ 5,2 Гал:

Центробежная сила на экваторе максимальна и равна ~ 3,4 Гал. В итоге: .

Для справки:

Выражение потенциала силы тяжести в виде ряда по сферическим функциям

Наше предыдущее рассмотрение, в итоге, оказалось ограниченным отражением лишь широтных зависимостей в геоиде. В принципе, необходимо, хотя бы формально, более полное рассмотрение. Такую картину дает следующее разложение потенциала:

Здесь – коширота: .

В этом представлении два первые члена – зональные гармоники, не зависящие от долготы; представляют Землю как тело вращения, характеризуют асимметрию Земли относительно экватора.

В двойной сумме: при n = k – секториальные гармоники. Остальные (n  k) члены суммы – тессеральные гармоники; отражают разделение сферы на сферические трапеции.

Вернемся к сфероиду Клеро: , где сжатие , – фигура равновесия планеты.

Сравним фигуру равновесия планеты с эллипсоидом вращения:

В сферических координатах ( – коширота) получим:

Здесь – сжатие.

Разложим это выражение в ряд по малой величине :

.

Заменив кошироту широтой  (), убедимся, что сфероид Клеро отличается от точного эллипсоида вращения членами порядка ² и выше.

Формула Клеро дает "простейшую" широтную зависимость g на сфероиде.

Сфероид второго приближения – сфероид Дарвина – Де-Ситтера:

,

где

В принципе, формул нормального распределения g было получено несколько. Наилучшей из них была (да и сейчас используется) формула Гельмерта (1901-1909):

Международным соглашением в 1930 г. была принята формула Кассиниса, "международная":

Сегодня эти формулы уже не являются лучшими. Большой прогресс связан со спутниками.

В 1971 г. Ассамблея МСГГ приняла формулу, которая называется референц-система 1967 г.:

Эта формула не сильно отличается от формулы Гельмерта, что позволило не пересматривать старые материалы съемок, особенно в нашей стране, где практически их обработка и была выполнена на основе формулы Гельмерта.

Естественно, что успехи гравиметрии продолжаются. В итоге, в 1979 г. на Генеральной Ассамблее МСГГ в Австралии принята новая система нормальной Земли с параметрами:

Конечно, и дальше будут уточнения, но кардинальных изменений ожидать не приходится.