Рабочие программы / Физика Земли / (6 сем) Гравитационное и магнитное поля Земли / [ Шашканов ] Лекции по гравитации / 2 - Масса и средняя плотность Земли

Масса и средняя плотность Земли

Точное знание массы Земли в абсолютных единицах крайне необходимо. Обычно массы планет и звезд выражаются в единицах массы Солнца, т.к. определяются на основании законов Кеплера.

Масса Земли может быть определена из теоремы Клеро: , где .

По системе 1979 г. имеем:

И следовательно: .:

Средняя плотность: .

(Если расчет массы проведен только по одному первому члену выражения для g_e, то получаем ).

Величина G известна с точностью до 0,1 %, все остальные параметры, а именно: , q, a – до 0,001 %. Значит, погрешность определения массы Земли здесь – 0,1 %.

Таким образом, гравиметрические данные позволяют "взвесить" Землю, т.е. выразить M в абсолютных единицах (или в единицах [GM ]). Знание же массы Земли в абсолютных единицах позволяет определить абсолютные величины масс и всех планет солнечной системы и самого Солнца.

Притяжение однородного сфероида

(Притяжение внутренней точки)

Задача решалась Маклореном, Лагранжем, Лапласом, Пуассоном и др.

В принципе, ситуация должна, особенно для сфероидов со слабым сжатием, быть похожей на случай однородного шара. Вспомним, какова обстановка с шаром.

1. Потенциал притяжения материального шара на внешнюю точку равен потенциалу, развиваемому материальной точкой, расположенной в центре шара и имеющей массу, равную массе шара (то же – и о силе притяжения).

2. Сила притяжения, развиваемая однородным шаром радиуса R на внутреннюю точку, отстоящую на расстояние  от центра шара ( < R), равна силе притяжения однородного шара радиуса (или эквивалентной ему точки в центре шара). Внешний по отношению к притягиваемой точке слой шара на эту точку не действует (теорема Ньютона).

3. Как следствие из 2) – Сила притяжения однородным шаром центра шара равна нулю.

Наметим ситуацию со сфероидом, тоже, конечно, однородным.

Уравнение сфероида, отнесенное к главным осям, можно записать:

Компоненты силы притяжения сфероидом внутренней точки P(x, y, z) с единичной массой имеют вид – рассмотрим на примере F_x-компоненты:

,

где ,  – плотность, d – элемент объема.

Расположим центр сферических координат в () P, причем полярную ось направим параллельно оси x. Тогда:

Тогда:

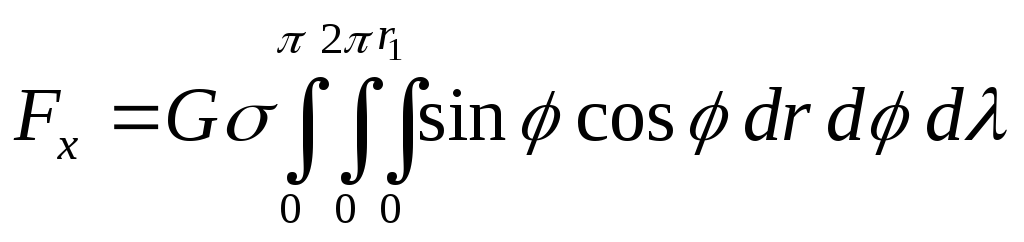
Здесь r₁ – радиус-вектор () с координатами (₁, ₁, ₁), расположенной на поверхности сфероида. Интегрируем dr:

6

r₁ здесь должно удовлетворять уравнению поверхности сфероида, а именно:

.

Для r₁ – это квадратное уравнение вида: , в котором:

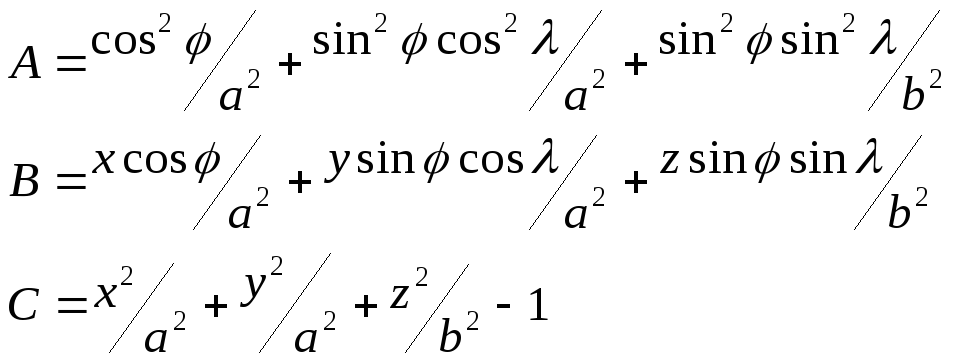
В итоге:

Коэффициент C для точек P(x, y, z) на поверхности сфероида равен нулю, внутри сфероида – C < 0. Поэтому дискриминант . Имеем два корня r₁, оставляем положительный:

И теперь подставляем его в 6.

В результате последующих преобразований в конце концов получаем:

.

Видим, что F_x зависит только от x и не зависит от y и z, т.е. F_x одинакова для всех точек плоскости x = const, параллельной плоскости yz. В выражение для F_x размеры сфероида входят в виде произведения a²A, т.е.:

,

куда истинные размеры сфероида a и b входят лишь в виде отношения . Это означает, что F_x, т.е. сила притяжения внутренней точки P(x, y, z) не изменится, если сфероид будет вместо a и b иметь полуоси и .

То же самое имеет место и для компонент силы F_y и F_z. Это означает, что сфероидальный слой, заключенный между соответствующими сфероидами и не оказывает никакого действия на внутреннюю точку. В итоге, имеем теорему:

Однородный слой, заключенный между поверхностями двух подобных и подобно расположенных сфероидов, не оказывает никакого действия на точку внутри этого слоя.

• Итак, имеем расширение упомянутой выше теоремы Ньютона для случая сферы.

Разовьем схему и запишем полную потенциальную функцию. Компоненты силы, действующей однородным сфероидом на внутреннюю точку, имеют вид:

, где

, где

e – второй эксцентриситет эллипса: .

Тогда 7

Т.к. при , то K₀ – это потенциал сфероида на свой центр. Простой расчет дает для K₀:

.

Фигуры равновесия гравитирующей вращающейся однородной жидкости

(Жарков § 55)

Рассматривая сфероид Клеро, как фигуру гидростатического равновесия для однородной планеты ( = ₀ = const), мы показали, что это фактически – эллипсоид вращения. Однако, этот результат является не приближенным, а точным. Кроме того, вообще говоря, возможен еще целый ряд устойчивых и метастабильных (неустойчивых) фигур равновесия вращающейся жидкости. Сделаем обзор этой картины.

Фигура равновесия жидкой массы должна иметь поверхностью эквипотенциальную поверхность: (вспомним ур-ие 7):

.

Необходимым условием существования равновесия во вращающейся гравитирующей жидкости, т.е. существования ее как некоего целого тела, является условие Пуанкаре: , где– _о – средняя плотность. Физический смысл этого условия примерно таков: гравитационные силы должны "стягивать" жидкость (для сложившейся формы) сильней, чем центробежное раскидывание – ее разрывать.

1. Рассмотрим сначала наиболее "естественный" случай эллипсоидальных фигур равновесия.

Найдем, какие ограничения накладываются на параметры вращающегося эллипсоида, если его поверхность – эквипотенциальная: W = const : (см. 7)

.

Здесь A, B, C, D – постоянные, определяемые размерами a, b, c эллипсоида. Анализ этого выражения показывает, что "условие" Пуанкаре приобретает более открытый смысл:

, 8

где – второй эксцентриситет эллипса.

Функция приведена на рисунке.

Максимум .

Ясно, что уравнение 8 имеет корни только при . При таком соотношении между плотностью ₀ и вращением  два сжатых эллипсоида являются точными фигурами равновесия вращающейся однородной жидкости – эллипсоиды Маклорена.

Если бы Земля была однородной с плотностью , то . Уравнение 8 тогда имеет два корня: e₁ = 0,092 и e₂ > 2,53, что соответствует эллипсоидам со сжатиями: (как у Ньютона для

 = const  = 1/231) и . Действительное сжатие Земли (), очевидно, соответствует первому корню. Отличие от ₁ обусловлено в основном неоднородностью плотности Земли.

Нетрудно видеть, что при . Значит, первый эллипсоид Маклорена вырождается в сферу, а второй, у которого сжатие ₂ стремится к единице, превращается в диск малой толщины большого радиуса, или, при  = 0 вырождается в бесконечно тонкую плоскость. Оба эллипсоида Маклорена вырождаются в один при e_m = 0,225.

Эллипсоиды Маклорена есть частный случай – фигуры вращения: a = b.

Но если , имеем эллипсоиды Якоби – трехосные равновесные эллипсоиды, тоже сжатые. Показано, что для них "условие" Пуанкаре еще строже:

При эллипсоид Якоби вырождается в бесконечно тонкую и бесконечно длинную иглу: .

Общая сводка:

1. При  = 0 существуют три предельные фигуры: сфера, плоский диск, вытянутая игла;

2. Если – имеем два эллипсоида Маклорена и один эллипсоид Якоби;

3. Если , то возможны только два эллипсоида Маклорена;

4. При – один предельный эллипсоид Маклорена;

5. При эллиптические фигуры равновесия невозможны.

2. О неэллипсоидальных фигурах равновесия

Математически, эллипсоиды Якоби есть как бы ответвления линейного ряда эллипсоидов Маклорена: существуя в окрестности последних.

Так, Александр Михайлович Ляпунов (1857–1918) доказал существование нетривиальных фигур равновесия вращающейся жидкости – особые фигуры. Примеры сложных фигур:

1. кольцо без центрального тела;

2. двойные (звезды) и кратные жидкие системы.

В последнее время определенное внимание уделяется трехосности Земли.

Автор	Год	Разность двух экваториальных радиусов: a1–a2, м	0 – долгота наибольшей оси
Гельмерт	1915	230 ± 51	17°W	Геодезические данные
Гейсканен	1929	165 ± 57	38°E
Изотов	1948	213	15°E
Гейсканен	1938	–	25°W
Гейсканен	1957	–	6°W	Гравиметрия
Грушинский	1961	–	25°E

Современные анализы дают: , т.е. говорить о трехосности Земли не приходится (тем более, что в условиях Земли эллипсоид Якоби должен быть сжат: a / b = 1,716 – типа сигары). Однако топография геоида реально несимметрична. Так, в акватории Тихого Океана имеется превышения геоида над сфероидом. Есть ли это факт трехосности Земли? – Вопрос требует дополнительных исследований.