Аномальное поле шара:

Аномальное поле горизонтального цилиндра, направленного вдоль оси у:

3. Вертикальная материальная линия (тонкий вертикальный стержень)

Рассуждая так же, как и в случае горизонтальной линии, и, соответственно, интегрируя от ₁ до ₂ при dl = d и полагая затем  =  = y = z = 0, получим:

.

При ₂ , т.е. когда нижний конец (край) нити залегает существенно глубже верхнего, имеем:

.

Для остальных производных гравитационного и магнитного потенциалов получим:

При z₂®¥:

.

.

Для магнитного поля:

.

.

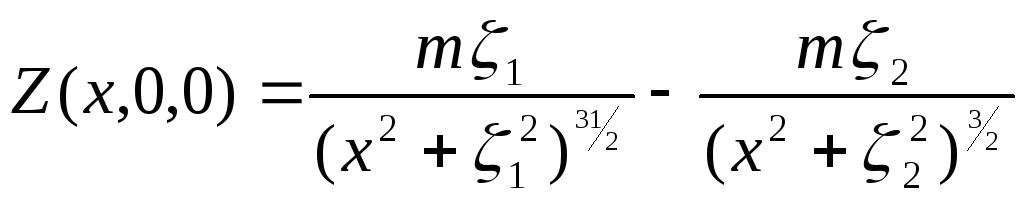Здесь – магнитные массы полюсов ( S – площадь поперечного сечения стержня. Исходим именно из площади стержня, а не длины, как в горизонтальном, потому, что «вектор» действия стержня теперь другой).

При ₂

.

.

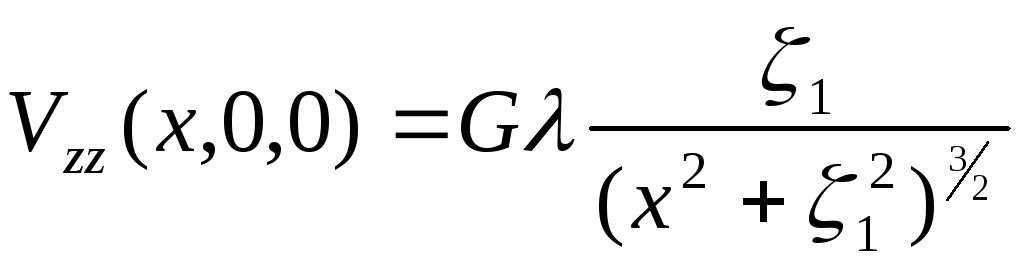Для магнитного поля:

.

.

Сравним выражение для Z(x,0,0) c выражением V_z(x,y,0) или лучше V_z(x,0,0) для шара:

. Из этого сравнения становится понятным физический смысл понятия магнитной массы m полюсов цилиндра – это «то же самое», что гравитационная масса (одиночного шара) в гравиметрии.

Для решения обратной задачи рассчитаем x_1/2 :

, откуда из выражения имеем: . В результате, имеем: и .

В случае вертикального цилиндра не всегда безразличен (по отношению к расчетам) его радиус R. В общем случае имеем: для точек конечного (₂ ) оси цилиндра, т.е. при x = 0 для максимума аномалии (V_z)_max получаем:

. ()

Нетрудно после этого записать формулу для (V_z)_max для кольца с внешним радиусом

R_внешн = R₂ и внутренним радиусом R_внутр = R₁:

Полагая в () , т.е. в формуле для диска, , получим: , – (), т.е. не зависящее от x и y поле (аномалию) от плоского (плоскопараллельного) горизонтального бесконечного слоя мощностью .

Частные случаи для конечного вертикального цилиндра :

а) при и R   на оси цилиндра имеет место:

, где  – поверхностная плотность диска,  – телесный угол видимости диска (с точки наблюдения);

б) при и, соответственно,  = 2 получаем: , что совпадает с ().