Рабочие программы / Физика Земли / (11 сем) Методы геофизической разведки / [ Каштан ] Печатные лекции / Прямая задача

Однородный по плотности шар

Для точек P(x,y,z), расположенных вне шара, притяжение равно притяжению материальной точки массой М, находящейся в центре шара.

В магнетизме это – вертикально и однородно намагниченный шар – центральный диполь. Учитывая предстоящее введение плоскости приведения, т.е. плоскости, для которой рассчитывается и анализируется поле, для силы притяжения (g = V_z) запишем:

.

Расположив плоскость приведения горизонтально, а начало координат – над центром шара и приняв z = 0, выражение для притяжения V_z в точке P(x,y,z) получим в следующем виде:

.

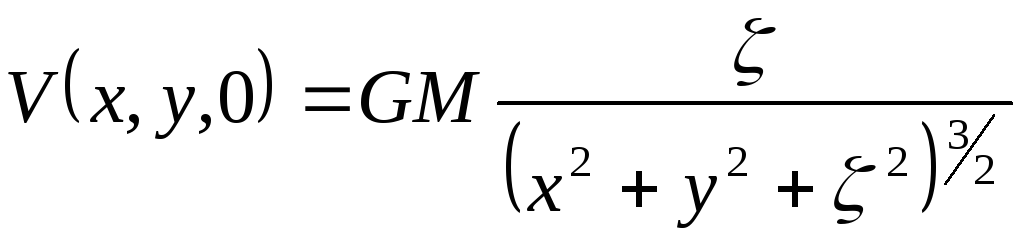При рассмотрении случая y = 0, имеем: x = 0 и

П родолжим дифференцирование, т.е. рассчитаем градиенты поля:

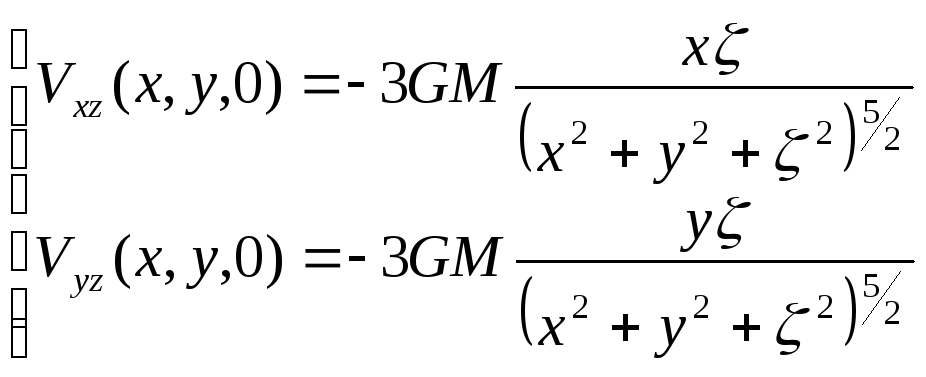; (1, 2)

аналогично:

. (3, 4, 5)

Учитывая вытекающие из теоремы Пуассона соотношения:

, для полей магнитных вертикально намагниченного шара имеем

(из соотношений 1, 2, 3 для V_zz, V_xz, V_yz):

.

Здесь M = JV₀ – магнитный момент шара (величина диполя).

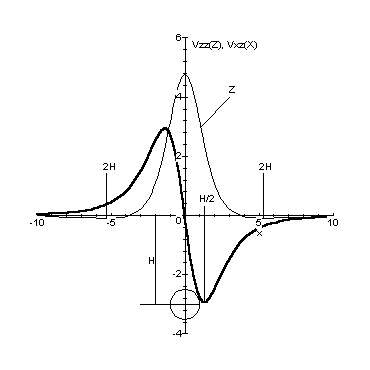
Проведем анализ кривых.

Для кривой V_xz или для северной компоненты Х магнитного поля:

экстремумы кривой расположены в точках:

и достигают в этих точках величин: (для меридионального градиента силы тяжести), или для магнитного поля).

Для кривой вертикального градиента силы тяжести V_яя, или для вертикальной компоненты Z магнитного поля:

максимум достигается в точке х = 0 и имеет значение: или ;

экстремумы кривой расположены в точках:

и достигают в этих точках величин: , или .

Отметим, что шару могут быть на практике уподоблены многочисленные объекты изометрической формы: рудные залежи гнездообразной и штокообразной форм (шток – тело неправильной формы, обычно – крутопадающее), солянокупольные структуры и др.

Рассмотрим на примере шара для случая гравиразведки возможность по результатам решения прямой задачи оценивать параметры возмущающего тела (основные параметры).

Для аномалии V_z , т.е. для аномалии силы тяжести:

1. Положение эпицентра тела определяется как центр «круговых» изолиний.

2. Найдем абсциссу х_1/2 точки, в которой сила тяжести в два раза меньше максимальной: 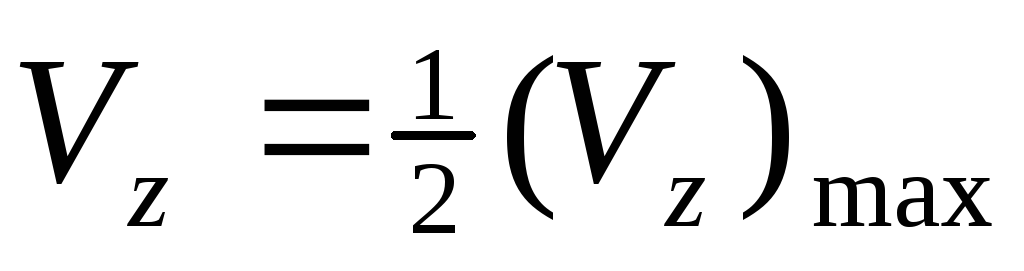(опять принимаем y = 0):

, откуда .

3.