Рабочие программы / Физика Земли / (11 сем) Методы геофизической разведки / [ Каштан ] Печатные лекции / 8 - Распределение аномального поля в пространстве и использование этого распределения при интерпретации

Распределение аномального поля в пространстве и использование этого распределения при интерпретации

I. Аналитическое продолжение позволяет построить картину распределения аномального поля во всем пространстве, за исключением особых точек.

Один из способов представления распределения аномального поля – построение карт изолиний аномального поля в вертикальной плоскости (вертикальные карты изолиний). При этом особенно целесообразно построение сечений, проходящих через экстремальные точки наблюденного аномального поля (и в крест простиранию – для двухмерных объектов).

Уравнение изолинии для тела простейшей формы можно получить, решив уравнения, выражающие соответствующие составляющие поля относительно х. Обозначим отношение величины этой составляющей к некоторой опорной характеристике аномалии (GM, M, 2G, M_s, 2G и т.д.) через р.

Рассмотрим, к примеру, шар (однополюсную магнитную массу):

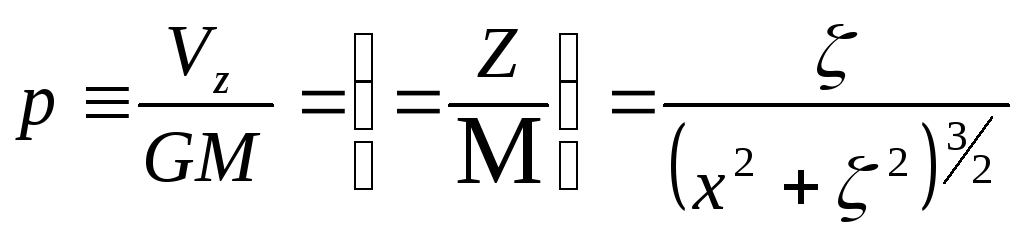, или , или, в итоге:

1) .

Аналогично:

Для горизонтального бесконечного кругового цилиндра (линии магнитных полюсов):

2) ;

для тонкого вертикального цилиндра:

3) ;

для полубесконечного вертикального цилиндра :

3,а) ;

для бесконечной горизоньальной материальной плоской полосы:

4)

для бесконечной материальной полуплоскости:

5) .

Построим вертикальные карты изолиний рассмотренных объектов:

Охарактеризуем картины изолиний рассмотренных объектов:

1. Особые точки тел являются и характерными точками семейств соответствующих изолиний, хотя и по-разному в разных телах.

2. Так, для шара и горизонтального цилиндра особые точки являются точками касания изолиний, а среди изолиний та, у которой р = 1,0 , касается дневной поверхности.

3. Для вертикального цилиндра его концы (т.е., особые точки) окружены изолиниями, причем, для полубесконечного – верхний конец окружен чистыми окружностями (концентрическими).

4. Для полосы это опять линии, пересекающиеся в особых точках, конкретно: окружности, общей хордой которых является сечение полосы плоскостью наблюдений.

5. Для бесконечной полуплоскости изолинии есть просто прямые линии, исходящие из ее края.

Естественно, что для тел простой формы иногда даже по части картины изолиний («изоаномал») в вертикальной плоскости, исходя из «фокусирующего действия» особых точек, можем определить положение этих точек, а значит, и соответствующих точек самих тел. Для тел более сложной формы поведение изолиний приобретает более сложный характер, однако опять фокусирующее действие особых точек сохраняется во всех случаях. В итоге, по поведению изолиний определяем местоположение «задающих» это сложное тело особых точек и тем самым – практически – форму и другие параметры возмущающего объекта.

II.

Применение аналитически продолженных значений аномального поля позволяет обощить метод характерных точек на случай пространственного распределения поля.

Вспомним, что при рассмотрении прямой задачи для тел простейших форм мы для силы тяжести V_z получали, например, для точек , в которых , соотношения типа: , где  – глубина объекта, а –коэффициент, разный для разных тел (и вообще: ). Однако можно «расширить» это рассмотрение:

_. ()

() –это уравнение семейства кривых, пересекающихся в особой точке, т.е. в точке с координатами: x = 0,  = 0.

Если возмущающие объекты характеризуются двумя и более особыми точками, то связи типа () получаются более сложными; аналитический вывод их затруднителен. В отдельных случаях, однако, это возможно сделать. Так для горизонтальной материальной плоскости (бесконечной полосы) шириной 2l для мы имели: . Это выражение есть уравнение равносторонней гиперболы, фокальная ось которой совпадает с проекцией полосы на вертикальную плоскость х0; расстояние между вершинами гипербол равно 2l , а асимптоты определяются уравнением: х = .

Учитывая указанные зависимости, можно для целей интерпретации строить и анализировать вертикальные карты изолиний абсцисс равных долей максимальных значений V_z.

Как это делается?: