







 ФИЗИКО-ТЕХНИЧЕСКИЙ
ФИЗИКО-ТЕХНИЧЕСКИЙ
ИНСТИТУТ
Кафедра «Общая и теоретическая физика»
Потемкина Л.О.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ №31
ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОГО МАЯТНИКА
Тольятти 2007
Содержание |
|
|
1. |
Цель работы.................................................................................................................................... |
3 |
2. |
Задачи работы................................................................................................................................. |
3 |
3. |
Приборы и принадлежности ......................................................................................................... |
3 |
4. |
Указания к самостоятельной работе............................................................................................. |
3 |
5. |
Краткие теоретические сведения.................................................................................................. |
3 |
|
5.1. Основные понятия и законы.................................................................................................. |
3 |
|
5.2. Математический маятник...................................................................................................... |
6 |
|
5.3. Вывод рабочей формулы....................................................................................................... |
6 |
6. |
Описание лабораторной установки и метода измерений........................................................... |
8 |
7. |
Программа работы ......................................................................................................................... |
8 |
8. |
Порядок выполнения работы........................................................................................................ |
9 |
2
1. Цель работы
Изучить основные закономерности малых колебаний математического маятника.
2.Задачи работы
1.исследовать зависимость периода колебаний от длины маятника;
2.ознакомиться с графическим методом определения ускорения свободного падения g.
3.Приборы и принадлежности
Установка, состоящая из штатива со шкалой, математического маятника и шарика, масса которого равна массе маятника.
4.Указания к самостоятельной работе
1.При домашней подготовке к лабораторному занятию необходимо по любому источнику (Савельев И.В., курс физики, т.1, или Трофимова Т.И., курс физики) проработать следующий материал:
1) Гармонические колебания и их характеристики. Т., §140. 2) Механические гармонические колебания. Т., §141.
3) Гармонический осциллятор. Т., §142. 4) Конспект лекций, 3 семестр, §§1 – 4.
2. Разобраться с выводом расчетной формулы к данной лабораторной работе.
3. Подготовиться к ответам на вопросы для тестового контроля к данной лабораторной работе.
5. Краткие теоретические сведения
5.1. Основные понятия и законы
Движения или процессы, характеризуемые определенной повторяемостью во времени назы-
ваются колебаниями.
Примеры колебательных процессов: качание маятника часов, переменный электрический ток. В первом случаи при колебательном движении маятника изменяется координата его центра масс, во втором – сила тока и напряжение в цепи.
В зависимости от физической природы колебаний различают колебания механические, электромагнитные и другие. Но различные колебательные процессы описываются одинаковыми характеристиками и одинаковыми уравнениями. Т.е. целесообразен единый подход к изучению колебаний различной физической природы.
Единый подход к изучению механических и электромагнитных колебаний применялся: английским физиком Д.У. Рэлеем (1842 - 1919 гг.), русским физиком А. Г. Столетовым, русским инженером экспериментатором П. Н. Лебедевым (1866 - 1912 гг.), Л. И. Мандельштамом и его учениками (1879 - 1944 гг.).
Колебания называются свободными (собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему.
Колебательной системой называется система, совершающая колебания. Простейшим типом колебаний являются гармонические колебания.
Колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса) называются гармоническими.
3
Рассмотрение гармонических колебаний важно по двум причинам:
1.колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому.
2.различные периодические процессы можно представить как наложение гармонических колебаний.
Гармонические колебания величины S описываются уравнением: |
|
S = A cos(ω0t +ϕ0 ) или S = A sin(ω0t +ϕ0 ) , |
(1) |
S = Smax cos(ω0t +ϕ0 ) или S = Smax sin(ω0t +ϕ0 ) , |
(2) |
где Smax = A – амплитуда колебания.
Максимальное значение колеблющейся величины, называется амплитудой колебания.
ω0 – круговая (циклическая) частота, собственных (свободных) гармонических колебаний;
ϕ0 – начальная фаза колебания в момент времени t = 0; (ω0t +ϕ0 ) – фаза колебания в момент времени t.
Что определяет фаза колебания? Фаза колебания определяет значение колеблющейся величины в данный момент времени.
Т.к. косинус изменяется от +1 до –1, то S изменяется от +А до –А, или от +Smax до –Smax.
Периодом колебания называется промежуток времени Т, за который фаза |
получает |
||||
приращение, равное 2π. |
|
|
|
|
|
Т.е. ω0 (t +T ) +ϕ0 −(ω0t +ϕ0 ) = 2π |
|
|
|
|
|
T = |
2π |
, |
(3) |
||
|
|
||||
|
ω0 |
|
|||
отсюда |
|
|
|
|
|
ω0 = |
|
2π |
. |
(4) |
|
|
|
||||
|
|
T |
|
||
Промежуток времени, через который повторяются определенные состояния системы, совершающей гармонические колебания называется периодом колебаний.
В СИ [T] = 1 с [ω0] = 1 рад/c = 1 c-1
Частотой колебаний называется число полных колебаний, совершаемых в единицу време-
ни: |
|
|
|
ν = |
1 |
. |
(5) |
|
|||
|
T |
|
|
В СИ [ν] = 1 Гц = 1 с-1 Величина, обратная периоду колебаний, называется линейной частотой колебаний.
1 Гц – частота периодического процесса, при которой за 1 с совершается один цикл процес-
са.
Сравнивая (3) и (4) получаем:
ν = |
ω0 |
(6) |
|
2π |
|
или |
|
|
ω0 = 2πν . |
(7) |
|
Найдем скорость и ускорение, с которым совершается данный колебательный процесс:
4
V = |
dS |
= S ′ = −Aω0 sin(ω0 t +ϕ0 ) |
= Aω0 |
cos(ω0 t +ϕ0 |
+ |
π |
) , |
|
(8) |
||||||||||
|
|
|
|
||||||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||
|
|
|
|
|
|
|
Vmax = Aω0 . |
|
|
|
|
|
|
|
|
|
(9) |
||
(9) – амплитуда скорости, т.е. скорость изменяется от +Vmax = +Aω0 |
|
до −Vmax = −Aω0 . |
|||||||||||||||||
a = |
dV |
= |
d 2S |
= −Aω2 |
cos(ω t +ϕ |
) = Aω2 cos(ω |
t +ϕ |
|
+π) , |
|
(10) |
||||||||
|
|
0 |
|
||||||||||||||||
|
|
dt dt2 |
0 |
0 |
0 |
|
0 |
0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
amax = Aω02 . |
|
|
|
|
|
|
|
|
|
(11) |
||
(11) – амплитуда ускорения, т.е. ускорение изменяется от |
+a = +Aω2 |
до −a |
max |
= −Aω2 . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
max |
|
0 |
|
|
|
0 |
||
Уравнение S′′+ω02S = 0 называют дифференциальным уравнением гармонических колебаний. Его решением является уравнение (1) или (2).
Пусть материальная точка совершает прямолинейные гармонические колебания вдоль оси координат х около положения равновесия, принятого за начало координат. Тогда:
|
|
|
|
x = Acos(ω0 t +ϕ0 ) . |
|
|
|
|||||
По определению: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V = |
dx |
= −Aω |
|
sin(ω t +ϕ |
) , |
|
||||
|
|
|
|
0 |
|
|||||||
|
|
|
|
dt |
|
|
0 |
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
a = |
dV |
|
d 2 x |
= −Aω |
2 |
cos(ω t +ϕ |
2 |
x . |
||||
|
= |
|
|
|
0 |
|
) = −ω |
|||||
|
|
|
|
|
||||||||
|
dt |
|
dt2 |
|
|
0 |
0 |
0 |
|
|||
|
|
|
|
|
|
|
|
|
||||
По второму закону Ньютона:
F = ma , и Fmax = mamax , тогда с учетом (14) получаем:
F = −mAω02 cos(ω0t +ϕ0 ) = −mω02 x .
(12)
(13)
(14)
(15)
Сила пропорциональна смещению материальной точки от положения равновесия и направлена в противоположную сторону к положению равновесия.
Fmax = −mAω02 . |
(16) |
Запишем выражения для кинетической, потенциальной и полной энергии материальной точ-
ки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По определению: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
E |
= |
mV 2 |
= |
mA2ω02 |
sin2 (ω |
t +ϕ |
) . |
|
(17) |
|||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
кин |
2 |
2 |
|
0 |
0 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Т.к. F |
= |
dEпот |
, то: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
E |
=−x |
Fdx=−x |
−mω2xdx= |
mω02x2 |
= |
mA2ω02x2 cos2 (ω02t +ϕ0) |
. |
(18) |
|||||||
|
|
|
|
||||||||||||||
|
|
|
пот |
∫ |
∫ |
0 |
2 |
|
|
|
|
2 |
|
||||
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
||||
|
+ E , тогда E = |
mA2 |
ω2 |
||
Но E = E |
|
0 |
, (19) т.к. m = const, ω0 = const, A = const, то следует |
||
2 |
|||||
кин |
пот |
|
|||
|
|
|
|||
вывод:
Вывод: Полная энергия остаётся постоянной, так как при гармоническом колебании справедлив закон сохранении механической энергии и упругая сила консервативна.
Система, совершающая колебания, описываемые уравнением вида: |
|
S′′+ω02S = 0 |
(20) |
5
(20) называется гармоническим осциллятором.
Колебания гармонического осциллятора являются важным примером периодического движения и служат точкой или приближенной моделью во многих задачах классической и квантовой физики.
Примером гармонического осциллятора являются: пружинный, физический, математический маятники, колебательный контур (для токов и напряжений столь малых, что элементы контура можно считать линейными).
5.2. Математический маятник
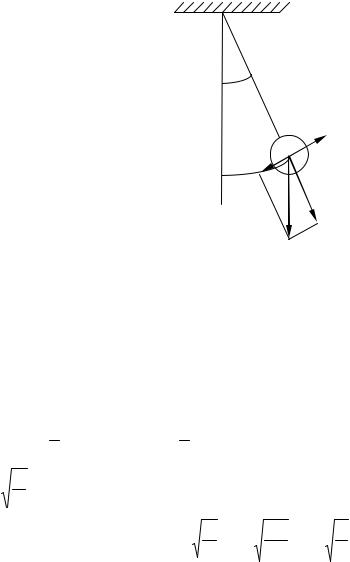
Идеализированная система, состоящая из математической точки массы m подвешенной на нерастяжимой невесомой нити и колеблющаяся под действием силы тяжести.
ϕl
х
_
Fв
_
mg
Рис. 1. Колебания математического маятника
Пример: небольшой тяжелый шарик, подвешенный на тонкой длинной нити.
mgG = N + Fв ,
где NG – сила реакции нити на натяжении, угол ϕ – мал,
х– путь, пройденный шариком.
x= lϕ или ϕ = xl ; тогда Fв = −mg xl
Но ω |
|
= k |
, а F = −kx , тогда mg |
x |
= kx k = |
mg |
. |
0 |
|
|
|||||
|
m |
упр |
l |
|
l |
||
|
|
|
|
||||
T = 2π |
m |
= 2π |
ml |
= 2π |
l . |
(21) |
|
k |
|
mg |
|
g |
|
|
x +ω02 x = 0 . |
|
|
(22) |
||
(22)– дифференциальное уравнение гармонических колебаний математического маятника.
5.3.Вывод рабочей формулы
Математическим маятником называют материальную точку, висящую на невесомой и нерастяжимой нити и совершающую колебания в вертикальной плоскости под действием силы тяжести. Это идеализированная физическая модель. На практике математическим маятником считают небольшое массивное тело, подвешенное на нити такой длиной, что размеры тела много меньше длины нити.
6
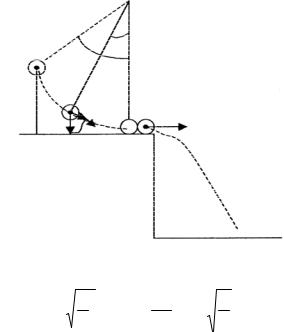
Если маятник отклонить от положения равновесия на угол α (рис. 2), то составляющая силы тяжести mg sin α стремится возвратить его к положению равновесия, создавая тангенциальное
ускорение: |
|
|
|
|
|
|
|||
|
|
|
|
aτ = ε l =α l , |
(23) |
||||
где l |
– длина нити маятника, |
|
|
|
|
|
|
||
ε |
– угловое ускорение. |
|
|
|
|
|
|
||
При этом: |
|
|
|
|
|
|
|||
|
|
|
|
maτ |
|
= mg sin α , |
|
||
или с учетом соотношения (23): |
|
|
|
|
|
|
|||
|
|
|
|
α + |
g |
sin α = 0 . |
|
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
l |
|
|
|
Обозначив |
g |
через ω02 и полагая для малых α |
sin α ≈α , получим дифференциальное |
||||||
|
|||||||||
|
|
l |
|
|
|
|
|
|
|
уравнение малых колебаний математического маятника: |
|
||||||||
|
|
|
|
α +ω02α = 0 |
|
(24) |
|||
решением которого будет закон гармонических колебаний: |
|
||||||||
|
|
|
|
α =α0 cos(ω0t +ϕ). |
(25) |
||||
α0 и ϕ0 – амплитуда и начальная фаза колебаний. |
|
|
|||||||
|
|
|
|
l |
α l |
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
α |
|
|
|||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
h |
|
|
|
mg sin α |
|
|
|
|
|
ατ |
1 2 |
ν |
|
|||
|
|
|
|
|
|||||
h1 S
|
|
|
Рис. 2 |
|
|
||
Частота и период колебаний |
|
|
|
|
|
|
|
ω0 = |
g |
; |
T0 |
= |
2π = 2π |
l |
(26) |
|
l |
|
|
|
ω0 |
g |
|
не зависят от амплитуды колебаний (изохронность) и массы маятника, а определяются только
2 |
|
4π 2 |
|
|
длинной нити l и ускорением свободного падения g. При этом T0 |
|
|
|
l , т.е. квадрат пе- |
|
||||
= |
g |
|
||
|
|
|
|
риода колебаний линейно зависит от длины маятника и тангенс угла наклона графика к оси абсцисс связан с g:
tg ϕ = |
4π |
2 |
, |
(27) |
g |
|
|||
|
|
|
|
что можно использовать для графического определения ускорения свободного падения g.
7
