4_Konspekt / Lekciya 25

Лекция 25

ФИЗИЧЕСКИЕ ОСНОВЫ ВИХРЕТОКОВОГО КОНТРОЛЯ

Рассмотрим возбуждающую (ВО) и измерительные (ИО) обмотки, расположенные над электропроводящим изделием. Переменное магнитное поле ВО приводит к появлению в изделии вихревых токов.

Плотность вихревых токов j максимальна на поверхности изделия в контуре, диа-

метр которых близок к диаметру ВО и убывает с увеличением r .

Плотность токов j убывает также с глубиной по закону j = j0 exp{−zδ}, причем

δ≤ 2ωµ0µσ,

где ω — частота тока в ВО; µ — относительная проницаемость; σ — удельная электриче-

ская проводимость материала, (Ом м)-1.

Взаимодействие преобразователя с изделием определяется соотношением, получае-

где ρ — избыточная плотность заряда, обычно при вихретоковом контроле равная нулю;

jпр =σE ; плотность переносного тока определяется выражением jперенос = σ{v × B}, где v

— скорость перемещения объекта контроля, в дальнейшем будем считать, что объект поко-

ится, или скоростью v можно пренебречь; токи смещения jсм существенны для диэлектри-

ков, поэтому ими будем пренебрегать; jстор — плотность токов, обусловленных действие

сторонних источников, будем считать, что такие источники отсутствуют. При указанных условиях первую пару уравнений (1) можно представить в виде

rot E = −µ′∂H∂t ;

Рассмотрим гармоническую плоскую электромагнитную волну, распространяющуюся в металле в направлении оси z , то есть H (z)= Hm (z)exp{iωt} и E (z)= Em (z)exp{iωt}

( i — мнимая единица), тогда

получим

rot rot Hm =ε′iω rot Em +σ rot Em =(σ+ε′iω)rot Em =(σ+ε′iω)(−µ′iω)Hm . (4)

Далее, вспомнив формулу двойного векторного произведения

{a ×{b ×c}}= b(a c)−c(a b),

можно записать

rot rot Hm ={ ×{ × Hm }}= ( Hm )− 2 Hm .

Так как

где {i, j, k} — тройка единичных векторов ортогональной системы координат (xyz), тогда

−∂Hmy ∂z ∂Hmx ∂z 0

Hmz = 0.

Так как компоненты Hmx и Hmy являются решениями одинаковых уравнений, рас-

смотрим первое из них. Решение ищем в виде

где k 2 =µ′σω(i −εω′ 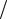σ). Так как электромагнитная волна в металле может только зату-

хать, то A2 =0 . Проанализируем выражение для k 2 . Его можно представить в виде

k 2 =µ′σω(i −εω′ σ)=µ′σω 1+(εω′ σ)2 exp{−i arctg 1(εω′ σ) }exp{iπ}.

Оценим значения параметров в этом соотношении для типичных материалов. Для ти-

уменьшается в e раз.

Для Hmy будем иметь аналогичное выражение.

Длину волны λ определим, приравняв

λ = 2π α= 2π 2 µσω′ .

Если электромагнитная волна падает на поверхность металла под углом ϑ0 , то в со-

ответствие с законом преломления угол распространения волны в металле ϑ равен

sin ϑ=(с1 с0 )sin ϑ0 ,

металле распространяется перпендикулярно его поверхности.

Рассмотрим магнитное поле во вторичной катушке ВТП — ИО. Полное электрическое сопротивление катушек характеризуется двумя величинами:

1. Индуктивное сопротивление — X L =ωL = 2π f L , где L — индуктивность ка-

тушки.

2. Омическое сопротивление — R .

Эти характеристики катушки откладываем на графике с координатами R – ωL .

В отсутствие испытываемого объекта пустая катушка имеет полное характеристиче-

ское сопротивление Z = R +iωL0 , которое показано на плоскости полного сопротивления

точкой P0 .

Если в поле катушки поместить испытываемый объект, то оно изменится под действием поля вихревых токов. Это изменение поля вызывает такой же эффект, какой получился бы, если изменить характеристики самой испытательной катушки. Таким образом, влияние испытываемого объекта может быть описано как изменение параметров катушки L1 и R1 —

точка P1 . Величина и направление смещения полного сопротивления от точки P0 к P1 явля-

ется функцией объекта и характеристик измерительного оборудования.

Важнейшим свойством объекта являются:

1.Электропроводность σ;

2.Размеры объекта (например, диаметр прутков, труб и т.п.);

3.Магнитная проницаемость µ;

4.Наличие несплошностей материала, таких как, трещины, раковины, включения

и т.п..

Важнейшими характеристиками оборудования являются:

1.Частота переменного тока;

2.Размеры и форма катушки;

3.Расстояние катушки до испытываемого объекта.

Все эти факторы влияют на полное сопротивление катушки. Зная изменение положение точки P и частоту можно в принципе определить все вышеуказанные параметры. Изменение характеристик катушки под влиянием объекта, можно описать, введя эффективную магнитную проницаемость, которая учитывает все вышеуказанные факторы.

Рассмотрим длинный цилиндр, помещенный внутри цилиндрической намагничивающей катушки, по которой течет переменный ток. Регистрирующая катушка находится внутри внешней.

Введем следующие допущения:

1. Внешняя катушка создает однородное магнитное поле H0 по всему сечению ка-

тушки.

2.Образец имеет бесконечную длину и постоянный радиус.

3.Электропроводность σ и проницаемость µ постоянны, хотя намагниченность

материала объекта меняется.

4. Различная интенсивность намагничивания возникает в результате экранирующего действия вихревых токов, которые создают магнитное поле противоположного направления.

Она может быть описана введением эффективной магнитной проницаемости µэфф .

5. Пренебрежем влиянием магнитного гистерезиса, считая, что он имеет малую величину и его влияние незначительно по сравнению с влиянием вихревых токов.

Запишем уравнения Максвелла:

где {er ; eϕ; ez } — реперная тройка векторов.

Так как задача радиально симметричная и поле H0 бесконечно вдоль оси цилиндра, то

∂ ∂ϕ=∂ ∂z = 0 , так как отсутствует зависимость параметров задачи от координат ϕ и z .

В этом случае магнитное поле имеет только одну компоненту H ={0; 0; Hz }, которая за-

висит от времени и радиуса Hz = Hz (r;t ). Из (8) следует, что отличной от нуля компонен-

той rot H является (rot H )ϕ. Из первого уравнения (7) следует, что у вектора E отлична от нуля только компонента Eϕ = Eϕ (r;t ), то есть E ={0; Eϕ;0}, и у rot E отлична от нуля

(rot E )z . В таком случае (8) примет вид

eϕ : −∂Hz ∂r =ε∂Eϕ ∂t +σEϕ ;

Из первого уравнения (9) находим

−∂H z ∂r = (ε∂ ∂t +σ)Eϕ ,

если обозначить L =(ε∂∂t +σ), то

Eϕ = −L−1 ∂Hz ∂r .

После подставки во второе уравнение (9)

Это уравнение Бесселя нулевого порядка. Общий вид уравнений Бесселя n -го порядка имеет вид

y′′+ y′ x −(1+ n2 x2 )y = 0 .

Общее решение этого уравнения

y(x)= AIn (x)+ B Kn (x),

где In (x) — функция Бесселя второго рода n -го порядка; Kn (x) — функция Кельвина n -

го порядка. Так как у нас n = 0 , то решение (10) имеет вид

Hm (kr )= AI0 (kr )+ B K0 (kr ).

Так как функция K0 (kr) при r → 0 имеет особенность K0 (kr )→∞, то из физических соображений следует, что необходимо положить B = 0 , тогда

Hm (kr )= AI0 (kr ).

Приведем для справок следующие формулы:

то есть

Hm (kr )= H0 I0 (kr)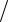I0 (ka).

Зависимость этой функции от параметров приведен на рисунке.

Магнитная индукции равна Bz =µ0µHm . Поток, пронизывающий вторую катушку и неферромагнитный образец, равен

Введем µэфф из условия, что по всему сечению образца действует поле H0 , но внут-

ри образца имеется комплексная проницаемость µэфф , такая что

Φобр =πa2µ0µэфф.H0 ,

Приравняв два последних соотношения, получим

a2µэфф ={2µ I0 (ka)} ∫a I0 (kr )rdr ,

0

откуда

µэфф ={2µ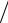a2 I0 (ka)} {rI1 (kr )k}0a = 2µI1 (ka)ka I0 (ka).

У нас ka = a ωµσ i = a ωµσeiπ4

Из теории специальных функций следует

In (x e±iπ4 ) e±iπn2 =bern (x)+i bein (x),

где bern (x) и bein (x) — специальные функции (см. Янке Е., Эмде Р., Леш Ф. «Специаль-

ные функции». — М.: Наука, 1968.). В нашем случае

I0 (xe±iπ4 )=ber0 (x)+i bei0 (x).

Частота, при которой ka =1 называется граничной частотой fg

ka = a ωµσ = a 2πfgµσ =1,

откуда

fg =12πσµa2 ,

следовательно, параметр, который определяет все характеристики в задаче — ka , в свою очередь, зависит только от отношения рабочей частоты f к граничной частоте fg :

ka = i f fg .

В частности, можно ввести относительную эффективную магнитную проницаемость

µ′эфф =µэфф µ = Φ(f fg )eiϕ(f fg ) =Φ1 (f fg )+i Φ2 (f fg ),

которая определяется отношением f fg .

Закон подобия

Таким образом, при равных значениях параметра ka или при равных значениях от-

ношения рабочей и граничной частоты f fg , распределение вихревых токов, магнитных

полей и наводимых ЭДС в двух экспериментах будет одинаково. Это утверждение носит название закона подобия. Этот факт используют для моделирования.

Последнее означает, что можно использовать результаты испытаний, полученные в удобных для проведения экспериментов условиях, для предсказывания характера влияния тех или иных факторов, не всегда поддающихся точному непосредственному изменению, на информативные параметры вихретокового контроля.

Например, заполняют ртутью форму из стекла, в которую вводят имитаторы дефектов из непроводящего материала. Полученные результаты обобщают, приводят к безразмерному виду и используют в дальнейшем при контроле реальных объектов. Таким образом, результаты испытаний на модели можно затем применить к испытуемому объекту с другими размерами, электропроводностью и относительной магнитной проницаемостью.

Влияние трещин в контролируемых образцах на изменение параметров измерительной катушки на основе этого закона можно изучать на образцах увеличенного сечения с искусственными дефектами, форма которых подобна трещинам.

ЭДС во вторичной катушке

При отсутствии образца во вторичной катушке наводится ЭДС холостого хода

Eхол = −ndΦdt ; Eхол = −inω(πd 24)µ0 H0 ,

то есть

Φ =(πd 2 4)µ0 H0 eiωt .

Абсолютное значение ЭДС холостого хода равно

Eхол = Eхол = 2π f n(πd 2 4)µ0 H0 ,

где n , d — число витков и диаметр вторичной катушки.

После ввода образца общий магнитный поток, созданный H0 , будет складываться из потока в образце и потока в зазоре. Доля ЭДС от потока в зазоре равна

Eз = −i 2π f nµ0 H0 (π4)(d 2 − d02 ), (d0 = 2a).