
4_Konspekt / Lekciya 5
.pdf
Лекция 5
АКУСТИЧЕСКИЕ СВОЙСТВА СРЕД
Свойства материалов, рассматриваемые с точки зрения распространения упругих волн, называются акустическими свойствами сред.
К основным акустическими свойствами сред относятся:
–скорости распространения продольных и поперечных волн;
–акустическое (волновое) сопротивление;
–затухание волн.
1.Скорости распространения продольных и поперечных волн относятся к основным характеристикам потому, что по ним могут быть вычислены скорость распространения дру-
гих видов волн, а также константы упругости материала, например, E и υ. Действительно,
так |
как c2 |
= E (1 −υ) ρ(1 +υ)(1 − 2υ) |
и c2 |
= E 2ρ(1 +υ), то |
отношение |
скоростей |
|
l |
|
t |
|
|
|
(cl |
ct )2 = 2(1 −υ) (1 − 2υ). Откуда |
υ= (cl ct )2 −2 2 ((cl |
ct )2 −1) , |
причем |
||
0 < υ<1 2 . Далее, если известна плотность, используя значение скорости, находим модуль Юнга E . Ниже приводятся значения скоростей продольные и поперечных упругих волн для металлов:
2 . Далее, если известна плотность, используя значение скорости, находим модуль Юнга E . Ниже приводятся значения скоростей продольные и поперечных упругих волн для металлов:
|
Металлы |
cl , м/с |
ct , м/с |
(4...6) 103 |
(2,5...3,5) 103 |
2. Значение волнового сопротивления или характеристический импеданс среды – ρc ,
определяет процессы на границах сред, связанные с отражением и прохождением волны. 3. Затухание упругих волн.
До сих пор мы пренебрегали затуханием (ослаблением) волн при их распространении. Однако во всех средах распространяющаяся волна затухает вследствие потерями энергии колебаний, связанными с неупругими свойствами сред и рассеянием на неоднородностях среды.
В самом общем случае с расстоянием амплитуда волны меняется по закону
A(x)= A0 exp{−δx}, где δ – коэффициент затухания – характеристика среды.
Коэффициент затухания складывается из двух составляющих δ =δn +δp , где
δп – коэффициент поглощения;
δр – коэффициент рассеяния.
При поглощении энергия волны переходит в тепловую и энергию внутренних степеней свободы структурных составляющих среды. При рассеянии преобразования энергии не происходит, она перераспределяется в среде в результате переотражения на неоднородностях среды, то есть часть энергии рассеивается в среде, что проявляется как уменьшение амплитуды в направлении первоначального распространения волны.
Примером может служить рассеяния УЗ-волны на зернах металла, имеющего поликристаллическое строение.
В жидкостях и газах поглощение обусловлено вязкостью и теплопроводностью, а также релаксационными процессами.
Вязкость среды – взаимодействие частиц среды друг с другом, трение слоев жидко-
сти и газа – сдвиговая вязкость.
Теплопроводность приводит к теплообмену между соседними сжатыми, а, следовательно, немного нагретыми, и разряженными (охлажденными) участками среды при распространении волны. Теплообмен вызывает понижение температуры в сжатом участке и уменьшение степени сжатия, охлажденные участки нагреваются и его растяжение уменьшается, так как уменьшается упругость среды. Эти процессы чередуются во времени (в течение одного периода) и в пространстве (на расстоянии длины волны), что приводит к переходу механической энергии волны в тепло, вследствие чего амплитуда волны уменьшается.
Релаксационные процессы (еще их называют объемной вязкостью) – эти процессы характеризуют потери механической энергии за счет обмена энергии между поступательными и внутренними степенями свободы частиц вещества, приводящего к установлению термодинамического равновесия между ними. В случае многоатомных газов и жидкостей передача упругой энергии волны от внешних (поступательных) степеней свободы к внутренним (колебательным и вращательным) происходит в течение некоторого времени τ, называемым временем релаксации – времени установления термодинамического равновесия между различными степенями свободы молекул, нарушенного при прохождении упругой волны.
Эти процессы вызывают запаздывание деформации среды относительно действующего напряжения (давления) в упругой волне. В среде могут происходить структурные изменения при ее периодическом растяжении и сжатии. Все эти изменения наиболее явно обнаруживаются в некотором интервале частот или на отдельных частотах, зависящих от температуры среды – релаксационный спектр. Поэтому на температурной или частотной зависимо-

стях появляются максимумы поглощения. Параметр τ подчиняется закону Аррениуса τ=τ0 exp{Q kT}, где τ0 ≈10−13...10−12 с; Q – энергия активации процесса; T – темпера-
kT}, где τ0 ≈10−13...10−12 с; Q – энергия активации процесса; T – темпера-
тура; k – постоянная Больцмана. Наиболее эффективно релаксационные процессы протека-
ют при выполнении условия ωτ 1, где ω – частота акустической волны. С учетом выра-
жения для τ получим ωτ=ωτ0 exp{Q kT} 1. Выполнение этого условия можно добить-
kT} 1. Выполнение этого условия можно добить-
ся, изменяя частоту волны, либо температуру среду, в которой распространяется волна. Последние осуществить гораздо проще, что часто используется при проведении экспериментальных исследований по изучению свойств газов, жидкостей и твердых тел.
Основные задачи, решаемые при помощи исследования релаксационных явлений: газы, пары – определение вязкости, коэффициента диффузии смесей, характеристики
внутренних степеней свободы молекул, констант в уравнениях состояния;
жидкости – изучение сжимаемости, определение уравнения состояния, исследование свойств теплоносителей, изучение кинетики протекания химических реакций;
твердые тела – широкий круг физических свойств, фазовые превращения в металлах и сплавах.
В жидкостях зависимость поглощения от частоты имеет вид:
δn f 2 ,
поэтому за характеристику среды принято считать величину, не зависящую от f ,
δ'n =δn f 2 ; |
δ'n |
H2 |
= 2,5 10−14 |
с2 |
м. |
|
|
0 |
|
|
В газах поглощение зависит как от частоты, так и от давления:
δn f 2  p ,
p ,
поэтому характеристикой среды служит величина
δ'n =δn p f 2 ; δ'n |
=1,25 10−6 |
Н с2 |
м3 . |
|
воздуха |
|
|
В твердых телах коэффициент поглощения обусловлен вязкостью среды и линейно растет с увеличением частоты:
δn =δ' f ,
где δ' −const, зависящая от структуры материала, а, следовательно, и от термообработки.
Рассеяние упругих волн в твердых телах
Металлы, применяемые на практике, имеют поликристаллическое строение. Падающая на границу зерен акустическая волна испытывает частичное отражение, преломление, при этом происходит трансформация волн, что и определяет механизм рассеяния.
Рассеяние приводит к образованию структурно реверберационных шумов, что существенно снижает чувствительность ультразвукового контроля. Доля рассеянной акустической энергии определяется главным образом отношением длины волны к среднему размеру
|
|
|
|
|
|
|
|
|
|
кристаллита D . |
|
|
|
|
|
|
|||
|
|
|
δ D3 f 4 |
λ |
D − релеевское рассеяние; |
|
|||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
λ D −стохастическое рассеяние; |
|
|
δрасс = δ2 D f |
|
||||||||
|
|
|
|
D |
|
λ |
D −диффузное рассеяние. |
|
|
|
|
|
δ3 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
Параметры δ1;δ2 |
и δ3 зависят от режима термообработки материала. |
||||||||
Для частот до 10 мГц, наиболее часто употребляемых для целее дефектоскопии, |
|||||||||
λ 0,5мм |
|
|
|
|
|
|
|
||
D, поэтому |
|
|
|
|
|||||
δ =δ' f +δ |
|
3 |
f 4 . |
|
|
||||
D |
|
|
|||||||
1 |
|
|
|
|
|
|
|||
Например, для алюминия δ' =0,84 10−7 с м и D3δ =3,7 10−28 c4 |
м. |
||||||||
|
|
|
|
|
|
|
|
1 |
|
Коэффициент рассеяния различен для разных типов волн. Зависимость коэффициента
затухания от D используют для контроля термообработки металлических изделий.
Так как, A(x)= A0 e−δx , отсюда δ =(1 x)ln A0
x)ln A0  A(x) , [δ]= м−1 . Смысл величи-
A(x) , [δ]= м−1 . Смысл величи-
ны 1 δ= x0 – расстояние, на котором амплитуда волны уменьшается в е раз. В технике для измерения затухания часто пользуются величиной – децибелом (дБ).
δ= x0 – расстояние, на котором амплитуда волны уменьшается в е раз. В технике для измерения затухания часто пользуются величиной – децибелом (дБ).
N (дБ)=10lg I0  I (x) ,
I (x) ,
где I |
– интенсивность акустической волны. Так как I A2 , то |
|
|||||
|
N (дБ)= 20lg A |
A(x) , |
|
|
|||
|
|
{ |
0 |
|
|
|
|
|
δ =(ln10 20x) |
20lg |
0 |
} |
δ' |
=(20 ln10)δ, так как |
|
тогда |
|
A |
A(x) . Введем |
||||
20 ln10 =8,685, то
ln10 =8,685, то
δ' (дБ/ м)=(1 x){20lg(A0
x){20lg(A0  A(x))},
A(x))},

таким образом, 1 дБ/м = (8,685)-1 м-1.
Кроме того, для измерения затухания применяется единица измерений Непер
N [Неп]=ln A0  A(x) .
A(x) .
Поскольку N = ln10lg A |
A(x) =(ln10 20) |
( |
20lg |
A |
A(x) |
, |
0 |
|
|
0 |
) |
|
то 1 Непер = (8,685)-1 дБ.
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ ВОЛН НА ГРАНИЦЕ СРЕД
Законы отражение и преломления ультразвуковых волн аналогичны законам отражения и преломления оптических волн. Однако имеется своя специфика вследствие того, что в твердых телах распространяются продольные и поперечные волны, а при прохождении и отражении от границы они могут трансформироваться друг в друга.
Рассмотрим прохождение продольной плоской волны через границу двух сред I и II, в
которых скорость распространения волны соответственно равна c1 и c2 , плотности сред ρ1
и ρ2 . Начало координат примем на границе сред. В среде I имеются падающая и отраженные волны, в среде II – только падающая волна. В среде I результирующее смещение определяется суммой двух волн падающей и отраженной
Ae−ik1x
C e−ik2 x
B eik1x
I |
0 |
I I |
x |
Нормальное падение плоской волны на границу двух сред
u1 (x; t )=(Ae−ik1x + B eik1x )eiωt ,
а акустическое давление – суммой
p1 (x; t )=iρ1c1ω(Ae−ik1x − B eik1x )eiωt .
Соответственно в среде I
u2 (x; t )=C e−ik2 x eiωt ,
p2 (x; t )=iρ2c2ωC e−ik2 x eiωt .

Условия на границе требуют равенства смещений (неразрывность среды) и равенство давле-
ний с обеих сторон – u1 =u2 и p1 = p2 . Из этих условий вытекает
A + B =C;
ρ1c1 (A − B)=ρ2c2C.
Обозначив zi =ρici , (i =1, 2)и ξ= z1  z2 , находим коэффициенты отражения по амплитуде смещения Ru – отношение амплитуды отраженной волны B к амплитуде падающей волны
z2 , находим коэффициенты отражения по амплитуде смещения Ru – отношение амплитуды отраженной волны B к амплитуде падающей волны
A, и прохождения по амплитуде смещения Du – отношение амплитуды прошедшей C вол-
ны к амплитуде падающей волны A:
Ru = B A =(1−ξ)
A =(1−ξ) (1+ξ); Du =C
(1+ξ); Du =C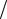 A = 2
A = 2 (1+ξ).
(1+ξ).
Аналогично с учетом выражений для акустического давления в средах находим коэффици-
енты отражения и прохождения по амплитуде давления Rp и Dp :
Rp = −Bρ1c1  Aρ1c1 = −Ru ;
Aρ1c1 = −Ru ;
Dp =Cρ2c2 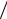 Aρ1c1 = 2ξ
Aρ1c1 = 2ξ (1 +ξ).
(1 +ξ).
Вспомнив определение силы звука – |
J =ρ c |
v 2 2 , |
а также взаимосвязь колебательной |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i i |
i |
|
скорости |
v |
и |
звукового |
давления |
p |
|
в |
плоской |
волне – vi = pi ρici , получим |
||||||
J = p 2 |
2ρ c . Далее можно записать выражения для коэффициентов отражения и прохо- |
||||||||||||||
i |
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
ждения для силы звука: |
|
|
|
|
|
|
|
|
|
|
|
||||
|
R = J |
отр |
J |
пад |
= |
p |
p |
|
2 |
= (1−ξ) (1+ξ) 2 ; |
|||||
|
|
J |
|
|
|
( |
отр |
пад ) |
|
|
|
|
|||
|
DJ |
= Jпрош |
Jпад = |
(pпрош |
pпад )2 (ρ1с1 ρ2с2 )= 4ξ (1+ξ)2 . |
||||||||||
Легко проверить справедливость равенства
RJ + DJ =1,
которое является следствием закона сохранения энергии. Заметим, что для других коэффи-
циентов отражения и прохождения это соотношение не выполняется. Выражения для RJ и
DJ симметричны относительно замены ξ→1 ξ, то есть доля энергии прошедшей через границу не зависит от направления прохождения волны. Отметим также, что все коэффициенты зависят только от отношения волновых сопротивлений сред.
ξ, то есть доля энергии прошедшей через границу не зависит от направления прохождения волны. Отметим также, что все коэффициенты зависят только от отношения волновых сопротивлений сред.
Рассмотрим некоторые частные случаи:
1. ξ 1 – волна распространяется из акустически жесткой среды в акустически мяг-
кую, например, из стали в воздух:
Ru =1, Du |
2 ; |
|
Rp = −1, |
Dp |
1; |
RJ =1, |
DJ |
0 . |
Другими словами весь поток акустической энергии практически отражается от границы раздела сред.
2. ξ 1 – волна распространяется из акустически мягкой среды в акустически жест-
кую, например, из воздуха в сталь:
Ru = −1, |
Du |
0; |
Rp =1, |
Dp |
2 ; |
RJ =1, |
DJ |
0 , |
то есть вновь поток акустической энергии практически весь отражается от границы раздела сред.
Прохождение волны через слой
Рассмотрим случай, когда акустическая волна падает нормально на поверхность слоя толщиной h . Окружающая слой среда имеет волновое сопротивление ρ1c1 , а вещество слоя
– ρ2c2 . Волна, падающая на верхнюю границу раздела, частично отражается от нею, и час-
тично проходит через границу. Волна, прошедшая слой, при падении на нижнюю границу раздела сред, в свою очередь, частично отражается от нее, и частично проходит в окружающую среду. Отраженная от нижней границы волна, распространяющая вверх, складывается с волной, прошедшей через верхнюю границу и движущуюся вниз. Происходит сложение волн. Волна, падающая на верхнюю границу снизу, также частично отражается от нее, и частично возвращается в верхнюю зону и т.д.

ρ1c1
x = 0
ρ2c2
x = h
ρ1c1
Нормальное прохождение плоской волны через слой
Мы описали последовательность процессов при прохождении волны через слой в терминах «падающая», «отраженная», «прошедшая» волна. Можно показать, что коэффициент отражения и прохождения силы звука в этом случае описывается выражением
|
RJ =(ξ2 −1)2 |
(ξ2 +1)2 + 4ξ2 ctg2 |
(k2h) ; DJ =1− RJ , |
|
|
|
|
|
|
где |
ξ =ρ2c2 / ρ1c1 = z2 / z1 ; |
k2 =ω/ c2 = 2π/ λ2. |
|
Поскольку ctg функция периодическая, |
RJ |
и DJ периодически зависят от произведения |
k2h = 2π(h λ2 ), то есть от отношения |
||
толщины слоя к длине волны в слое. Если толщина слоя равна целому числу полуволн h = nλ2 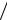 2 , n =1,2,..., то ctg(2πnλ2 / 2λ2 )=ctg πn →∞ и RJ →0 , а DJ =1. Полувол-
2 , n =1,2,..., то ctg(2πnλ2 / 2λ2 )=ctg πn →∞ и RJ →0 , а DJ =1. Полувол-
новой слой прозрачен для падающих волн независимо от волновых сопротивлений сред. Минимальное значение коэффициента прохождения имеет место при максимуме отражения
min{DJ }=1−max{RJ },
в свою очередь, max{RJ } достигается при h =(λ2  4)(2n +1), n = 0,1,2,... :
4)(2n +1), n = 0,1,2,... :
max{RJ }= (ξ2 −1) (ξ2 +1) 2 .
(ξ2 +1) 2 .
Кроме того, если 2ξctg(k2h) (ξ2 +1), то RJ →0 и DJ →1. Другими словами,
при малых h слой прозрачен для акустических волн УЗ. Например, воздушный зазор в стальном изделии прозрачен на частоте 1 МГц при h ≤10−6 мм, а масляная прослойка при h ≤ 2 10−2 мм. Это используют для повышения эффективности ввода ультразвуковых колебаний, располагая тонкий слой масла, между объектом контроля и пьезопреобразователями, либо приклеивая их тонким слоем клея к объектам контроля. В то же время УЗ-волны прак-

тически полностью отражаются от тончайших 10-5…10-4 мм несплошностей металла. Зави-
симость DJ от отношения h λ2 для разных сред показана на рисунке.
λ2 для разных сред показана на рисунке.
Рассмотрим численный пример. Пусть в стальной конструкции имеется внутренняя, раскрытая, плоская трещина. Допустим, при ультразвуковом контроле плоская акустическая волна падает нормально поверхности трещины, которая полностью перекрывает ее. Оценим долю энергии акустической волны, прошедшую через трещину. С точки зрения прохождения волны трещину можно рассматривать, как газовый слой в стали. Будем полагать, что раскрытие трещины достаточно велико в выше указанном смысле, а газ в трещине – воздух. УЗволна проходит через две границы сталь-воздух и воздух-сталь. Отношение волновых сопротивлений сред равны ξ(сталь воздух) 105 и ξ(воздух
воздух) 105 и ξ(воздух сталь) 10−5 . С учетом вы-
сталь) 10−5 . С учетом вы-
ражения для DJ можем записать
(DJ )трещ = DJ (сталь воздух)DJ (воздух
воздух)DJ (воздух сталь)
сталь)
4 ξ(сталь воздух) 4ξ(воздух сталь) =1,6 10−10 |
; |
||
|
|
|
|
(RJ )трещ =1 −(DJ )трещ |
1. |
|
|
Таким образом, трещина практически полностью отражает падающую на нее акустическую волну. Это – основа УЗ-дефектоскопии, регистрируются параметры акустические волны, отраженных от дефектов – трещин, пор и т. п., или характеристики прошедших волн, ослабленные этими дефектами.
Можно показать, что, если слой окружают разные среды, такие что максимальное прохождение наблюдается при h =(λ2  4)(2n +1).
4)(2n +1).

z1 =ρ1c1
x = 0
z2 =ρ2c2
x = h
z3 =ρ3c3
Нормальное прохождение плоской волны через слой, разделяющий разные среды
В этом случае говорят о четверть волновом просветленном слое. При падении на границу звукового импульса и учета затухания волн в слое расчеты показывают, что осцилля-
ции RJ и DJ уменьшаются по мере роста h / λ2 . Это объясняется уменьшением амплитуды колебаний интерферирующих волн по мере увеличения h . Поэтому для того, чтобы добиться оптимального просветления границы на практике, следует брать наиболее тонкий про-
светляющий слой h =λ2 4 .
Наклонное падение волн на границу раздела сред
Если волна падает на границу двух сред наклонно, то отраженная и прошедшая волны преломляются, трансформируются в продольные и сдвиговые волны, распространяющиеся под разным углом.
Наклонное падение плоской волны на границу двух твердых сред
Углы падения, отражения и преломления волн, подчиняются закону Снеллиуса
