
4_Konspekt / Lekciya 8
.pdfЛекция 8
ЭКВИВАЛЕНТНАЯ СХЕМА И АКУСТИЧЕСКОЕ ПОЛЕ ПЬЕЗОИЗЛУЧАТЕЛЯ
В пьезоэлектрической среде связь между электрическими и механическими величинами, выражается с помощью уравнений пьезоэффекта, и приводит к взаимодействию упругих и электромагнитных волн.
При анализе распространения волн в пьезоэлектрике в принципе нужно решать одновременно уравнения Ньютона и Максвелла. Решения представляют собой смешанные упру-
го-электромагнитные волны, то есть упругие волны со скоростью cзв , сопровождаемые элек-
трическим полем, и электромагнитные волны со скоростью распространения с 105 cзв , со-
провождаемые механической деформацией.
Для первого типа волн можно пренебречь магнитным полем, которое создается пере-
менным электрическим полем, перемещающимся со скоростью cзв , малой по сравнению со
скоростью электромагнитных волн. Тогда согласно уравнению Максвелла
rot E = −∂B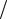 ∂t 0 ,
∂t 0 ,
и электрическое поле E выражается, как в электростатике, через скалярный потенциал Φ,
т.е. E = −grad Φ. В результате оценки показывают, что электромагнитная энергия пренеб-
режимо мала по сравнению с упругой энергией. Для второго типа волн упругая энергия оказывается пренебрежительно малой по сравнению с электрической.
Таким образом, даже в сильных пьезоэлектриках взаимодействие между упругими и электромагнитными волнами оказывается весьма слабым из-за большой разницы соответст-
вующих скоростей с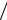 cзв 105 . Следовательно, распространение волн можно рассматривать без учета электромагнитных эффектов, в предположении, что поле является электростатическим, то есть в квазистатическом приближении.
cзв 105 . Следовательно, распространение волн можно рассматривать без учета электромагнитных эффектов, в предположении, что поле является электростатическим, то есть в квазистатическом приближении.
Из уравнения пьезоэффекта имеем:
Tij =CijlmE Slm −epij Ep .
После подстановки выражения для тензора деформации получим
Slm =(1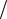 2)(∂ul
2)(∂ul 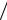 ∂xm +∂um
∂xm +∂um 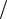 ∂xl )
∂xl )
и для пьезостатического электрического поля —
Ep = −∂Φ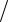 ∂xp .
∂xp .

В результате с учетом симметричности Slm можно записать
Tij =cijlmE ∂ul ∂xm +epij ∂Φ ∂xp .
Из уравнения Ньютона
∂Tij ∂xj =ρ∂2ui ∂t2 ,
после подстановки выражения для Ti j будем иметь
cE |
∂2u |
∂x |
∂x +e |
pij |
∂2Φ ∂x |
∂x |
p |
=ρ∂2u |
∂t2 , ( i, j,l,m, p =1,2,3 ). |
(1) |
|
ijlm |
l |
j |
m |
|
j |
|
i |
|
|||
Для электрической индукции получим следующее соотношение: |
|
||||||||||
Dk |
=eklmSlm +εkpS Ep |
=eklm (∂ul |
∂xm )−εkpS |
(∂Φ ∂xp ). |
(2) |
||||||
Для непроводящей среды индукция должна удовлетворять уравнению Пуассона |
|
||||||||||
div D = 0 , |
|
|
|
|
|
|
|
|
|
||
или |
|
|
|
|
|
|
|
|
|
|
|
∂Dk ∂xk |
=0 . |
|
|
|
|
|
|
|
|
||
После подстановки (2) получим |
|
|
|
|
|
|
|||||
eklm (∂2ul |
∂xk ∂xm )−εkpS |
(∂2Φ ∂xk ∂xp )= 0. |
(3) |
||||||||
Уравнения (1) и (3) описывают распространение упругих волн в пьезоматериале. Ре-
шая эту систему с соответствующими начальными и граничными условиями для u и E , можно описать распространение упругих волн в пьезоэлектриках.
Эквивалентная схема пьезопреобразователя
Пьезоэлектрический преобразователь представляет собой систему, в которой электрические и механические характеристики взаимосвязаны. Изменение механической нагрузки на преобразователь изменяет его электрические параметры, и наоборот, электрическое шунтирование преобразователя влияет на его механические свойства.
Если рассматриваются продольные или толщинные колебания преобразователя, то можно использовать эквивалентную схему в виде шестиполюсника, соответствующая наличию у преобразователя двух механических и одной электрической пары выводов,
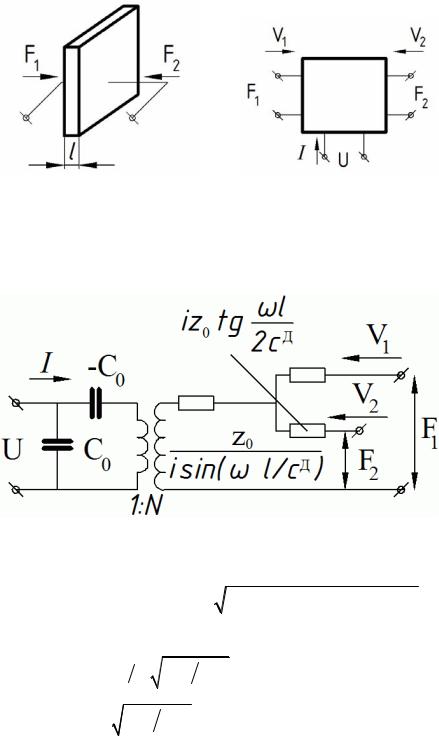
В широком интервале частот эквивалентную схему преобразователя в форме пластины можно представить в виде
Здесь введены следующие обозначения:
Z0 =ρпCnSn ; C0 =εSn 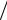 l ; Cn = E (1−υ)
l ; Cn = E (1−υ)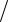 ρ(1+υ)(1−2υ);
ρ(1+υ)(1−2υ);
размерный коэффициент трансформации электромеханического трансформатора:
Nпл =C0h33 =(S l ) |
(c33D β33S |
)Kt — для пластины; |
Nст =C0h33 = (εT33 |
S33E )K33 |
— для стерженя. |
Схема, построенная на основе анализа уравнений механических колебаний преобразователя в одномерном приближении с учетом влияния электрического поля.
Наличие элемента « −C0 » — отрицательной емкости, отражает включение формально вводимого и не имеющего физического смысла импеданса Z0 = −1/ iωC0 . Описанную вы-
ше схему можно анализировать как электрическую, постоянная сила поджимающая преобразователь не учитывается.
Если преобразователь нагружен только с одной стороны, а сила на другой стороне равна нулю, то на схеме это отражается замыканием одной пары механических контактов. Возбуждающая сила оказывается приложенной ко второй паре и компенсируется инерционной силой колебаний преобразователя.
Приведенную схему удобно использовать в следующих случаях:
а) анализа сигналов пьезопреобразователя, работающего в импульсном режиме, когда существенна роль переходных процессов;
б) анализа режима нерезонансного возбуждения, когда излучается спектр собственных колебаний объекта в широкой полосе частот.
Первый случай характерен для УЗ-дефектоскопии, когда осуществляется ударное возбуждение пьезоизлучателя короткими импульсами. Второй — используется в спектроскопических методах.
Режим работы пьезопреобразоват в качестве резонатора
Рассмотрим работу пьезопластины в качестве резонатора.
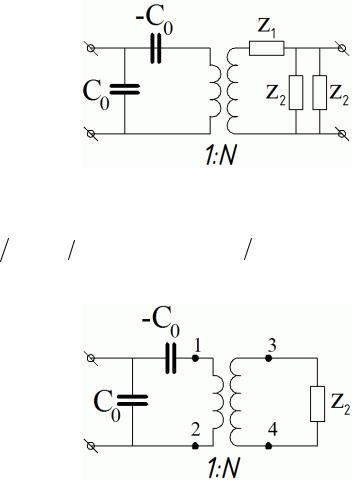
Эквивалентную схему пластины в этом случае можно получить, закоротив два механических выхода общей эквивалентной схемы. Здесь введены обозначения
Z1 = Z0 isin (ωl c), |
Z2 =i Z0 tg(ωl 2cD ). |
Эта схема эквивалентна: |
|
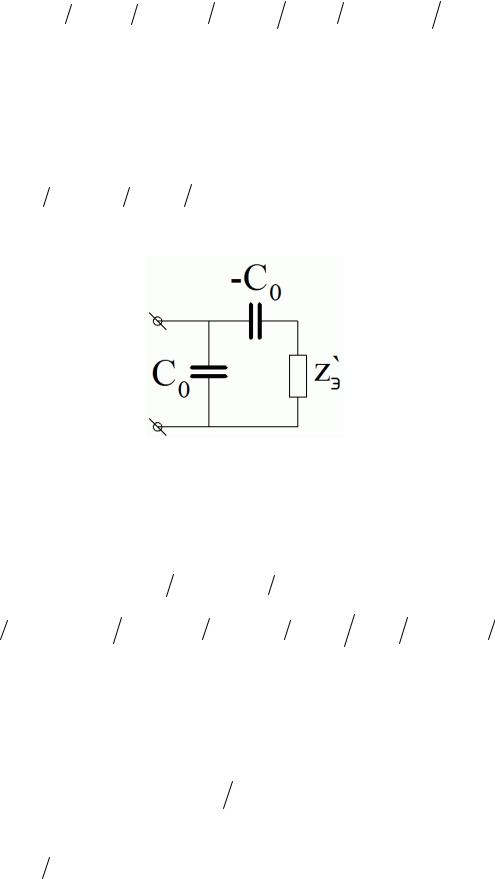
На этом рисунке |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
э |
1 |
|
2 |
|
0 |
|
{ |
|
( |
|
|
) |
|
( |
|
} |
|
0 |
|
( |
|
) |
|
Z |
+ Z |
2 =(iZ |
2) |
|
tg |
ωl |
2cD |
−2 sin |
ωl cD |
) |
= −iZ |
2 tg |
ωl / 2cD |
. |
||||||||||
|
= Z |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Пересчитаем Zэ в первичную обмотку. В соответствии с законом сохранения энергии можно записать U12 I12 =U34 I34 , следовательно,
U34 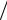 U12 = N , I12
U12 = N , I12 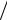 I34 = N
I34 = N
Учитывая, что U34 = ZэI34 , получим
U |
12 |
=U |
34 |
N = Z I |
34 |
N = Z |
э |
N 2 I |
, |
|
|
э |
|
12 |
|
тогда Zэ′ = Zэ / N 2 .
Окончательно входной импеданс преобразователя определяется как
1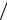 Zвx =iωC0 +1
Zвx =iωC0 +1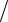 (Zэ′ −1
(Zэ′ −1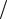 iωC0 )=iωC0 +iωC0
iωC0 )=iωC0 +iωC0 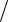 (iωC0Zэ′ −1).
(iωC0Zэ′ −1).
Отсюда
Zвx =(1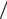 iωC0 ) (iωC0Zэ′ −1) iωC0Zэ′ =(1 iωC0 ) (Zэ′ −(1
iωC0 ) (iωC0Zэ′ −1) iωC0Zэ′ =(1 iωC0 ) (Zэ′ −(1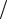 iωC0 ))
iωC0 ))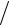 Zэ′ =
Zэ′ =
0 |
) |
{ |
|
0 |
( |
|
) |
0 |
} |
|
|
0 |
( |
|
) |
=(1 iωC |
|
−iZ |
|
2N 2 tg |
ωl 2cD |
|
−(1 iωC |
) |
|
−iZ |
|
2N 2 tg |
ωl 2cD |
= |
=(1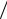 iωC0 ){1−(2N 2
iωC0 ){1−(2N 2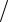 ωC0Z0 ) tg(ωl
ωC0Z0 ) tg(ωl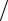 2cD )}.
2cD )}.
Далее, можно записать
2N 2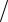 ωC0Z0 = 2N 2 (l / 2cD )
ωC0Z0 = 2N 2 (l / 2cD )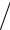 C0Z0 (ωl / 2cD ) =
C0Z0 (ωl / 2cD ) =
=(N 2l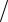 C0Z0cD ) 1 (ωl / 2cD ) = K 2
C0Z0cD ) 1 (ωl / 2cD ) = K 2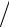 (ωl / 2cD ),
(ωl / 2cD ),
где через K 2 обозначен квадрат коэффициента электромеханической связи
K 2 = N 2l C Z |
cD . |
(4) |
|
0 |
0 |
|
|
В результате всех преобразований получим, что
Zвx =(1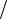 iωC0 ){1− K 2 tg (ωl
iωC0 ){1− K 2 tg (ωl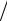 2cD )
2cD )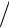 (ωl
(ωl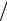 2cD ) }.
2cD ) }.
Таким образом, Zвx зависит от ω. При малых (ω→0) Zвx имеет емкостной характер
Zвx |
(1− K 2 ) iωC0 1 iωC0 , |
так как K 2 |
1. Величину, обратную Zвx |
Y =1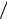 Zвx ={iC0ω
Zвx ={iC0ω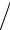 ωl 2cD − K 2 tg (ωl 2cD ) } (ωl
ωl 2cD − K 2 tg (ωl 2cD ) } (ωl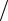 2cD ),
2cD ),
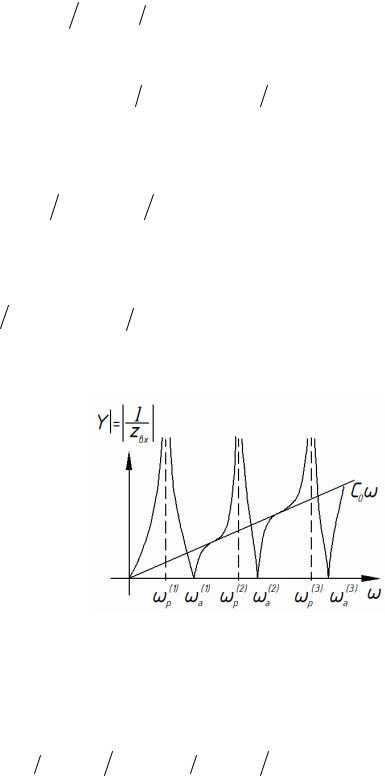
называют адмитансом. Частоты, на которых Zвx |
обращается в нуль, а Y →∞, называются |
|
резонансными частотами. Уравнение для нахождения резонансных частот имеет вид |
||
K 2 tg(ω(pn)l 2cD )=ω(pn)l |
2cD . |
(5) |
Частоты, на которых Zвх →∞, а Y →0 , называются антирезонансными. Они определяют- |
||
ся из условия tg → ∞, то есть |
|
|
ω(n)l 2cD =π(2n −1) 2 , |
n =1,2.... |
|
a |
|
|
На рисунке показана зависимость адмитанса от частоты.
Первая антирезонансная частота равна
ω(a1) = πcD 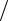 l .
l .
После подстановки в (5) получим
K 2 tg (π 2) (ω(pn) ω(a1)) =(π 2) (ω(pn) ω(a1)). |
(6) |
Определив экспериментально частоту антирезонанса ω(a1) = 2πfa(1) , можно рассчитать ско-
рость распространения звука в пьезоматериале: cD = 2l fa(1) .
Далее, зная первую резонансную частоту, можно согласно (6) определить квадрат коэффици-
ента электромеханической связи K 2 :
K 2 =(π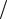 2) (f p(1)
2) (f p(1)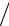 fa(1))ctg (π
fa(1))ctg (π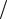 2) (f p(1)
2) (f p(1)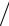 fa(1)) =
fa(1)) =
=(π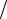 2) (f p(1)
2) (f p(1)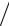 fa(1))tg{(π
fa(1))tg{(π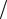 2) (fa(1) − f p(1))
2) (fa(1) − f p(1))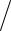 fa(1) } (π2
fa(1) } (π2 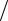 4) (fa(1) − f p(1))
4) (fa(1) − f p(1))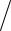 f p(1) ,
f p(1) ,
причем
∆f 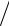 f р(1) =(fa(1) − f p(1))
f р(1) =(fa(1) − f p(1))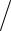 f р(1) 1.
f р(1) 1.
Эквивалентная схема пьезопреобразователя вблизи резонансной частоты
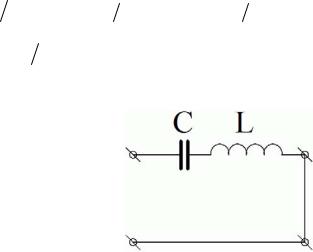
Покажем, что вблизи резонансной частоты эквивалентную схему пьезопластины можно представить в виде последовательной LC цепочки. Поскольку
Zэ′ = −i Z0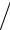 N 2 2 tg(ωl
N 2 2 tg(ωl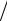 2cD ) ,
2cD ) ,
при стремлении ω→ω(a1) =πcD 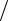 l — частота первого антирезонанса, близкая к частоте первого резонанса, Zэ′ →0 . Обозначив ω1 = ω(a1) и введя расстройку ε =(ω−ω1 )
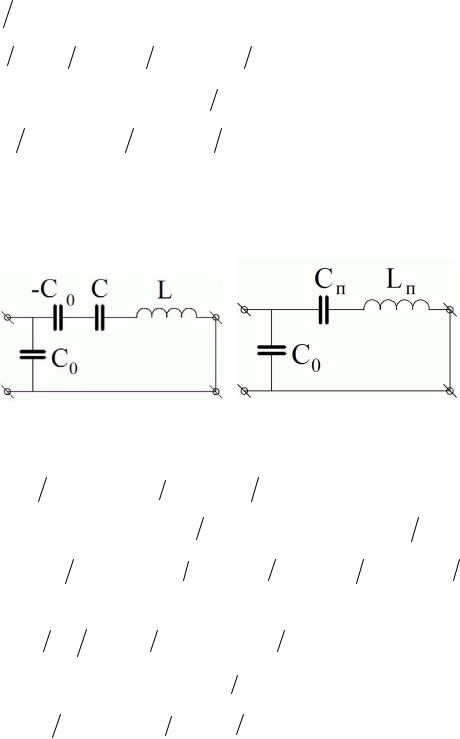
l — частота первого антирезонанса, близкая к частоте первого резонанса, Zэ′ →0 . Обозначив ω1 = ω(a1) и введя расстройку ε =(ω−ω1 )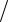 ω1 1,
ω1 1,
вблизи антирезонанса можно записать
сtg |
( |
ωl 2cD |
) |
= сtg (π 2)(1+ε) |
−πε 2 ; |
|
|
|
|
|
|
||
Zэ′ =(i πZ0 |
4N 2 )ε. |
|
(7) |
|||
Покажем, что аналогичный импеданс имеет последовательная LC -цепочка.
Действительно, импеданс этой LC -цепочки равен
Zц =iωL +1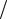 iωC =i(ω2CL −1)
iωC =i(ω2CL −1)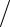 ωC .
ωC .
Обозначив ω21 =1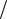 LC — резонансная частота цепочки, и вводя расстройку
LC — резонансная частота цепочки, и вводя расстройку
ε =(ω−ω1 ) ω1 1, вблизи резонанса Zц можно представить в виде |
|
Zц =(i ωC )(ω ω1 +1)(ω ω1 −1) (2i ω1C )ε= 2i Lω1ε. |
(8) |
Здесь учтено, что, поскольку ω≈ω1 , то (ω ω1 +1) |
2 . Сравнивая (7) и (8), находим |
L = πZ0 8N 2ω1 ; C =1 Lω21 =8N 2 πZ0ω1 . |
(8) |
Тогда эквивалентная схема преобразователя приобретает вид, показанный на рисунках, причем
Cn = −C0C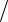 (C −C0 )=C
(C −C0 )=C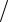 (1−C
(1−C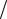 C0 ).
C0 ).
Так как N =C0h33 , то согласно (8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
C =8C2h2 |
πZ |
0 |
ω |
1 |
; |
|
С С =8C h2 |
πZ |
ω |
1 |
. |
|
|
|
|
|
||||||||
0 |
33 |
|
|
|
|
|
|
|
|
0 |
|
0 |
33 |
0 |
|
|
|
|
|
|
|
|||
Подставив N в (4), находим |
K 2 =C h2 l |
Z |
cD . С учетом того, что ω l |
cD =π, получаем |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
33 |
0 |
|
|
|
|
|
|
1 |
|
|
|
|
C =C0 8C0h332 πZ0ω1 =C0 (8 π) (C0h332 l Z0cD ) (cD lω1 )=(8K 2 π2 )C0 , |
||||||||||||||||||||||||
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cn = (8 K 2 |
|
π2 ) |
(1 −8 K 2 π2 ) C0 |
|
(8K 2 |
π2 )C0 , |
|
|
|
|
(9) |
|||||||||||||
так как K 2 1. Далее, учитывая, что |
C |
=εS l , после подстановки |
Z |
0 |
и ω |
1 |
в (8) находим |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||
L = L =πZ |
0 |
8N 2ω |
1 |
=ρS |
п |
l 8N 2 = m 8N 2 , |
|
|
|
|
|
|
|
(10) |
||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где m =ρSп l — масса пьезоэлемента; N =C0h33 = h33 εS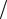 l .
l .
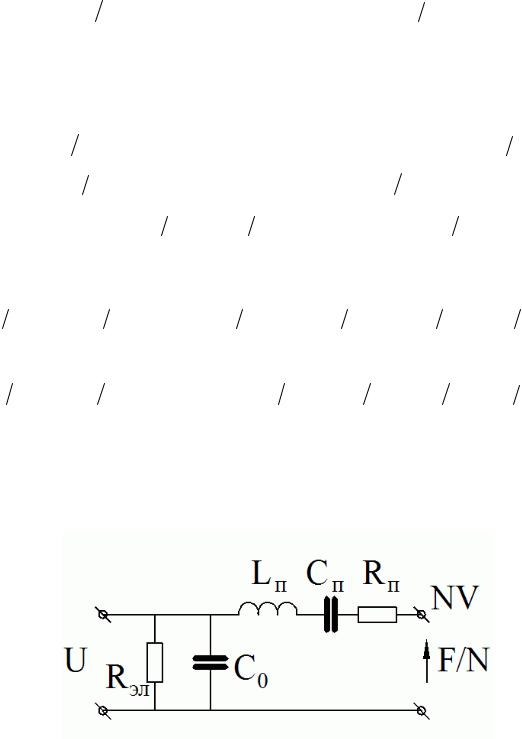
Чтобы иметь представление о порядке величин, рассчитаем Cn и Ln для эквивалент-
ной схемы тонкой круглой пластины из пьезокерамики ЦТС-19, работающей в резонансном
режиме. |
|
|
Выберем следующие параметры пластины: |
|
|
l =3 10−3 м — толщина; |
d =5 10−3 м — диаметр; |
|
ρ=7 103 кг м3 — плотность; |
h =1,7 109 |
B м — пьезомодуль; |
|
33 |
|
ε33отн. =1,5 103 — относительная диэлектрическая проницаемость;
K0,5 — коэффициент электромеханической связи.
Врезультате расчетов по (9) и (10) находим:
Sп = πd 2 |
4 =1,96 10−5 м2 ; |
ε33 =ε0εотн. =1,33 10−8 Ф м; |
|
C0 =ε33Sп |
l =87 пФ; |
Cn =(8K 2 π2 )C0 =17,6nФ; |
|
N =C h |
=0,15 ФB м=0,15 H B ; |
L = 2,29 10−3 Вс А= 2,29 10−3 |
Гн. |
0 33 |
|
н |
|
Здесь учтены следующие взаимосвязи между единицами величин:
при расчете параметра N
(Ф B м= Кл B с м B с = A B с м B = Вт с м В = Дж м В = Н В);
при расчете параметра Lп
(кгВ2 Н2 =(кгм с2 )(В2с2 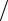 Н2 м)= В2с2 Дж = В2с Вт = В2с АВ = Вс А= Гн).
Н2 м)= В2с2 Дж = В2с Вт = В2с АВ = Вс А= Гн).
Расчетные параметры используются при разработке измерительной аппаратуры для обеспечения максимальной чувствительности контроля.
Мы рассмотрели эквивалентную схему пьезоэлемента без учета затухания. Более реальному случаю отвечает схема, в которой эти потери учитываются.
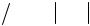
Здесь C0 — собственная емкость пьезопластины при U = 0 , то есть емкость зажатого пре-
образователя; Rэл — сопротивление диэлектрических потерь, ими, как правило, пренебре-
гают; Rn = r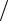 N 2 — сопротивление, учитывающее потери на внутреннее трение в материале преобразователя Q−1 .
N 2 — сопротивление, учитывающее потери на внутреннее трение в материале преобразователя Q−1 .
Величины Rn и Ln связаны через добротность преобразователя Q =1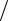 Q−1
Q−1
Rn =ωp Ln / Q .
Добротность, в свою очередь, определяется из соотношения
Q 1 ωp C0 Zmin .
На резонансной частоте ULn =URn , и преобразователь эквивалентен конденсатору
C0 , шунтированному Rn и импедансом излучения (акустической нагрузки), пересчитанной в электрическую часть преобразователя, — Zн =(F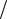 V )(1
V )(1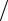 N 2 ), где V — колебательная
N 2 ), где V — колебательная
скорость излучаемой (регистрирующей колебания) поверхности пьезопреобразователя; F
— переменная сила, действующая на эту поверхность. В частности, а) если излучающий пьезопреобразователь в форме пластины плотно прижат или при-
клеен к поверхности массивного объекта контроля, характерные размеры которого h (20...30)λ, где λ — длина излучаемой воны, можно считать, что волна излучается в
бесконечную среду, тогда акустический импеданс нагрузки
Zн =(F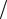 V )(1
V )(1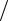 N 2 )= (ρc)ср S (1
N 2 )= (ρc)ср S (1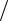 N 2 ),
N 2 ),
где (ρc)ср — волновое сопротивление среды; S — площадь поверхности преобразователя-
пластины.
б) если в объекте контроля происходит отражения волн с образованием стоячих волн,
то импеданс нагрузки Zн =(F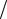 V )(1
V )(1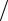 N 2 ) — комплексный, что, вообще говоря, усложняет
N 2 ) — комплексный, что, вообще говоря, усложняет
анализ эквивалентной схемы.
АКУСТИЧЕСКОЕ ПОЛЕ ПЬЕЗОИЗЛУЧАТЕЛЯ
ВУЗ-дефектоскопии вводятся следующие понятия:
1.Поле излучения.
