
- •Основные понятия и определения.
- •Анализ рычажных механизмов.
- •Структурный анализ механизма.
- •§1.2 Определение числа степеней свободы рычажных механизмов.
- •Пространственные механизмы.
- •Кинематический анализ рычажных механизмов. Основные понятия и определения.
- •Основными задачами кинематического исследования движения звеньев механизма являются:
- •1.Построение диаграммы перемещения.
- •Построение графиков скорости и ускорения по графику перемещения.
- •Метод планов скоростей и ускорений.
- •Планы ускооений
- •Механизмы с высшей кинематической парой.
- •Условие существования высшей кп.
- •Кинематика высшей кп.
- •Эвольвента и ее свойства.
- •§4.4 Элементы эвольвентного зубчатого колеса.
- •Основные расчетные зависимости для определения параметров эвольвентного зубчатого колеса.
- •Виды зубчатых колес.
- •§4.5 Эвольвентная зубчатая передача и ее свойства (рис. 11-86).
- •Основные расчетные зависимости для определения основных параметров эвольвентных зубчатых передач.
- •Качественные показатели зубчатых передач.
- •Определение коэффициента перекрытия графическим способом.
- •Способы изготовления зубчатых колес
- •Понятие о производящем исходном контуре реечного инструмента.
- •Станочное зацепление.
- •Основные расчетные зависимости для определения параметров зубчатого колеса, исходя из схемы станочного зацепления.
- •Специальные передаточные (планетарные) механизмы.
- •Сравнительный анализ передачи с неподвижными осями планетарной передачи.
- •Определение передаточного отношения планетарных механизмов различных схем. Планетарный однорядный механизм (механизм Джеймса).
- •Планетарный механизм со смешанным зацеплением (с одним внешним и одним внутренним зацеплением).
- •Механизм с двумя внешними зацеплениями.
- •Планетарный механизм с двумя внешними зацеплениями.
- •Кулачковые механизмы.
- •§6.1 Основные схемы кулачковых механизмов.
- •Кулачковый механизм с поступательно движущимся толкателем.
- •Понятие об угле давления.
- •Вывод формулы для определения угла давления в кулачковом механизме.
- •Синтез (проектирование) кулачковых механизмов по заданному закону движения толкателя.
- •Построение закона движения оси толкателя.
- •Определение минимального радиуса кулачковой шайбы по известному закону движения толкателя.
- •Построение профиля кулачка.
Понятие об угле давления.
Угол давления– угол между вектором линейной скорости выходного звена (толкателя) и реакцией, действующей с ведущего звена (кулачка) на выходное звено. Эта реакция без учета сил трения направлена по общей нормали к взаимодействующим поверхностям. Угол давления определяется экспериментально. Для кулачкового механизма с поступательно движущимся толкателем допустимый угол давления равен:[θ] = 25º÷35º.
Для кулачкового механизма с качающимся толкателем допустимый угол давления равен: [θ] = 35º÷40º.

Реакцию можно
разложить на две составляющие:
![]() и
и![]() .
.
Если, в силу
каких‑либо причин, угол давления
будет увеличиваться, то
![]() будет уменьшаться, а
будет уменьшаться, а![]() –
увеличиваться.
–
увеличиваться.
При достижении углов больше допустимого, возможен перекос оси толкателя в направляющей.
Вывод формулы для определения угла давления в кулачковом механизме.
И з
треугольникаΔКВР:
з
треугольникаΔКВР:
![]() (1)
(1)
КР = О1Р – О1К = О1 – е
КВ = so + sB
![]() (2)
(2)
Треугольник ΔО1ВР подобен треугольникуΔАВС.Тогда
![]()
![]()
vB1= ω1·O1B
![]()
Подставим это выражение в (2):
![]()
Знак “ – ”– для правой внеосности;
знак “ + ”– для левой внеосности.
Угол давления в кулачковом механизме зависит от размеров кулачковой шайбы: чем она больше, тем угол давления меньше.
Понятие об отрезке кинематических отношений.
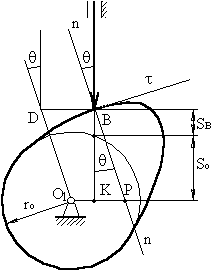
Если из точки Вдля какого‑то текущего положения толкателя проведем линию, параллельнуюО1Р, а из центра –|| nn, то при их пересечении получим точкуD:
BD = O1P = vB2 / vB1 =vqB2
Из рисунка следует, что перемещение точки Втолкателя и, найдя максимальный отрезок кинематического отношения, можно определить положение центра вращения кулачка, отложив внешним образом от точкиDдопустимый угол давления.
Синтез (проектирование) кулачковых механизмов по заданному закону движения толкателя.
Под синтезом кулачкового механизма будем понимать построение профиля кулачка, в каждой точке которого угол давления не превышал бы допустимого, а размеры самого профиля были бы минимальны.
Данная задача решается в 3 этапа:
Строится график заданного закона движения (как правило либо график ускорения точки Втолкателя как функция угла положения –aB = f(φ1), либо график линейной скорости точкиВ–vB= f(φ1)). Требуется построить график перемещения точкиВкак функцию от угла поворота кулачкаsB= f(φ1).
Определение минимального размера кулачковой шайбы при условии, что угол давления в любой точке профиля не превышает допустимого.
Построение профиля кулачка.
Построение закона движения оси толкателя.
Дано: Надо построить:
вид графика aB
= f(φ1),
![]() графикиaB
= f(φ1)
графикиaB
= f(φ1)
максимальный ход vB= f(φ1)
толкателя hт sB= f(φ1)

b– база графика (сколько отводиться на график по осиφ1).
Порядок построения:
Произвольно выбирается база графика.
Считаем масштаб по оси φ1:
![]() ,
мм/град
,
мм/град
Если задан симметричный вид графика, то:
φуд = φсб bуд = bсб
В общем случае закон движения может быть несимметричным.
Зададимся произвольным образом а1= 40 ÷ 50 мм. Тогда
а2= а1/ν
Возникает вопрос: каким должно быть расстояние х?
Его находят из условия равенства площадей под и над осью φ1.

Почему надо выдерживать равенство площадей?
Физический смысл площади под кривой ускорения на площадке х– скорость толкателя на данном участке.
Физический смысл площади под кривой скорости на участке φуд– максимальное удаление (перемещениет.Втолкателя). Если площади не будут равновеликими, то толкатель, поднявшись на одну величину, опустится на другую.
Построив график ускорения, строим график скорости методом графического интегрирования, выбрав отрезок интегрирования ОК1. Интегрируя график скорости (с отрезком интегрированияОК2, обычноОК1=ОК2), получаем график перемещения т.Втолкателя. Полученную ломаную линию заменяют плавной кривой.
Расчет масштаба:
(уSВ)maxна графике перемещений получается автоматически, и его величина зависит от отрезкаОК2. Тогда, зная ход толкателя, масштаб перемещения будет:
μ=![]()
Затем в первом приближении принимаем, что кулачок вращается равномерно, тогда угол поворота кулачка пропорционален времени поворота, и оси φ и tсовпадают, но каждая ось имеет свой масштаб.
![]()
где b– в[мм]; частота вращения кулачкаn – [об/мин];φраб – [град].
Масштаб скорости:
![]()
Масштаб ускорения:
![]()
