§2.8. Примеры и задачи

2.8.1. Синусоидальные величины и их символическое изображение

Мгновенные значения синусоидальной величины определяются выражением:

с = Аm sin(ωt +ψ ) = A 2 sin(ωt +ψ ) ,

где Am – амплитуда;

A– действующее значение;

ω= 2π f – угловая частота, [с-1];

f = 1T – линейная частота, [Гц];

T– период колебаний [c];

ψ– начальная фаза, [рад].

Расчет цепей переменного тока облегчается, если изображать гармонические токи, напряжения и ЭДС векторами на комплексной плоскости.

Совокупность векторов, изображающих синусоидальные функции в заданный момент времени, называется векторной диаграммой.

+j

Комплексное число может быть представлено в алгебраической и показательной форме:

A = ae jψ = b + jc .

Переход из показательной формы в алгебраическую форму осуществляется по формуле Эйлера:

ae jψ = acosψ + j asinψ = b + jc .

Комплексная синусоидальная функция представляется в виде вращающегося вектора на комплексной плоскости:

Мгновенное значение синусоидальной функции есть проекция вращающегося вектора на мнимую ось:

16

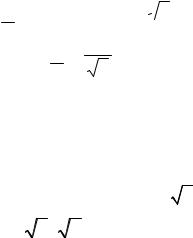
с = Im( ~c ) .

Обозначения:

i, u, e – мгновенные значения тока, напряжения, ЭДС.

Im, Um, Em – комплексные амплитудные значения тока, напряжения, ЭДС. I, U, E – комплексные действующие значения тока, напряжения, ЭДС.

Примеры

U m = 100e j300 = 50 3 + j50 = 86.6 + j50 ;

U= 1002 e j300 = 61.2 + j35.5 .

1.2.Комплексное действующее значение тока I = 5 − j5 .

Записать выражение для мгновенных значений тока. Решение:

I = 5 − j5 = 5 2 e− j45° ;

частотой и амплитудой.

Записать выражения i1(t) и i2 (t) для случаев: i2 опережает ток i1 на угол π / 3;

i2 отстает от тока i1 на угол π / 6 ;

i2 находится в противофазе с током i1 ; i2 совпадает по фазе с током i1 .

1.2. Ток i1 изменяется по синусоидальному закону. Частота f = 50 Гц, амплитуда

Im1 = 2,3 А, начальная фаза ψ1 = 180° . Ток i2 изменяется по синусоидальному закону с той же частотой и амплитудой.

Записать выражения i1(t) и i2 (t) для случаев: i2 совпадает по фазе с током i1 ;

i2 отстает от тока i1 на угол 30° ; i2 опережает ток i1 на угол 130° ;

17

i2 находится в противофазе с током i1 .

Построить графики i2 (t) .

1.3. Ток i1 изменяется по синусоидальному закону. Период T = 20 мс, амплитуда

Im1 = 3 2 A, начальная фаза ψ i = π / 3. Ток i2 изменяется по синусоидальному закону с той же частотой, но амплитуда в два раза больше.

Записать выражения i1(t) и i2 (t) для случаев: i2 опережает ток i1 а угол π / 4 ;

i2 отстает от тока i1 на угол π / 6 ;

i2 находится в противофазе с током i1 ;

i2 совпадает по фазе с током i1 . Построить графики i2 (t) .

1.4. Ток i1 изменяется по синусоидальному закону. Период T = 40 мс, амплитуда Im1 = 2,8 A, начальная фаза ψ i = −30° . Ток i2 изменяется по синусоидальному закону с той же частотой и амплитудой.

Записать выражения i1(t) и i2 (t) для случаев: i2 опережает ток i1 на угол 30° ;

i2 отстает от тока i1 на угол 40° ;

i2 находится в противофазе с током i1 ;

i2 совпадает по фазе с током i1 . Построить графики i2 (t) .

1.5. Заданы мгновенные значения токов:

i1 = 1,7 sin(ωt − 210°) , i2 = 2,4 sin(ωt + 190°) , i3 = 2,6 sin(ωt − 18°) , i4 = −4,7 sin(ωt − 45°) , i5 = 3,1 sin(ωt + 10°) .

Записать комплексные мгновенные, амплитудные и действующие значения токов в алгебраической и показательной формах.

Построить векторы комплексных действующих значений токов на комплексной плоскости. 1.6. Заданы мгновенные значения токов:

i1 = 1,25 sin(ωt − π2 ) ,

18

i2 = 2,41 sin(ωt + π3 ) ,

i3 = 2,6 sin(ωt − 43π ) , i4 = −3,5 sin(ωt − 45π ) ,

i5 = −1,4 sin(ωt + 23π ) .

Записать комплексные мгновенные, амплитудные и действующие значения токов в алгебраической и показательной формах.

Построить векторы комплексных действующих значений токов на комплексной плоскости.

1.7. Заданы мгновенные значения токов:

i1 = −2,5 sin(ωt) , i2 = 3,4 sin(ωt + 10π ) , i3 = 4,6 sin(ωt − π8 ) , i4 = 5,1 sin(ωt + 23π ) ,

i5 = −3,2 sin(ωt − 23π ) .

Записать комплексные мгновенные, амплитудные и действующие значения токов в алгебраической и показательной формах.

Построить векторы комплексных действующих значений токов на комплексной плоскости.

1.8. Заданы мгновенные значения токов:

i1 = 1,41 sin(ωt − 60°) , i2 = 4,51 sin(ωt + 15°) , i3 = 2,8 sin(ωt − 150°) , i4 = 2,4 sin(ωt − 260°) , i5 = −3,5 sin(ωt + 90°).

Записать комплексные мгновенные, амплитудные и действующие значения токов в алгебраической и показательной формах.

Построить векторы комплексных действующих значений токов на комплексной плоскости.

1.9. Заданы комплексные действующие значения токов и напряжений:

I1 = − j25 ,

U1 = 120 ,

19

I2 = −10 − j10 , U2 = 120 + j120 .

Построить векторы токов и напряжений на комплексной плоскости. Записать мгновенные значения i(t) и u(t) .

1.10. Заданы комплексные действующие значения токов и напряжений:

I1 = 10 − j10 ,

U1 = 5 + j5 , I2 = − j5,

U2 = j100 .

Построить векторы токов и напряжений на комплексной плоскости. Записать мгновенные значения i(t) и u(t) .

1.11. Заданы комплексные действующие значения токов и напряжений:

I1 = 6 + j8 ,

U1 = 110e jπ ,

I2 = 10e− j60° ,

U2 = 5 + j12 .

Построить векторы токов и напряжений на комплексной плоскости. Записать мгновенные значения i(t) и u(t) .

1.12. Заданы комплексные действующие значения токов и напряжений:

I1 = 10e j36° ,

U1 = 110e jπ ,

I2 = 7,07 − j7,07 , U2 = 100e jπ .

Построить векторы токов и напряжений на комплексной плоскости. Записать мгновенные значения i(t) и u(t) .

1.13. Заданы комплексные действующие значения токов и напряжений:

I1 = 8 + j6 ,

U1 = 100e jπ / 2 , I2 = 10e j2π / 3 ,

U2 = 5 + j12 .

Построить векторы токов и напряжений на комплексной плоскости. Записать мгновенные значения i(t) и u(t) .

20