
Физика Лабораторный практикум. Часть 1 (2005)
.pdf
|
|
|
|
|
m 2 |
|
2 R 2 |
|
g 2 |
|
2 t |
2 |
|
h |
2 |
||||
I |
1 |
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и его |
|
|
|
|
|
|||||||||||||||
|
1 |
|
|
m |
|
R |
|
g |
|
|
|
|
h |
|
|||||
|
|
|
|
|
|
|
t1 |
|
|||||||||||
относительную погрешность: I1 ∙100%. Записать окончательный
I1
результат для первого значения момента инерции маятника Обербека: I1=(<I1>±∆I1) кг∙м2.
III.ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.Какое движение называется вращательным движением?
2.Записать основное уравнение динамики вращательного движения. Пояснить входящие в уравнение величины, их единицы измерения.
3.Что называется моментом инерции тела относительно оси вращения? От каких величин зависит момент инерции тела? В каких единицах он измеряется?
4.Как определяется момент инерции тела правильной геометрической формы относительно оси, проходящей через центр масс?
5.Как определяется момент инерции тела относительно оси, не проходящей через центр масс? Сформулировать и записать теорему Штейнера.
6.Дать определение момента силы относительно оси вращения. Записать формулу, единицу измерения.
7.Что называется вращающим моментом? Какая сила приводит тело
квращению?
8.Дать определение углового ускорения. Записать формулу, единицу измерения. Изобразить на рисунке вектор углового ускорения.
9.Какова связь между угловым ускорением тела и касательным ускорением точек тела?
10.Записать уравнение динамики поступательного движения падающего груза.
IV. СОДЕРЖАНИЕ ОТЧЕТА
1.Титульный лист.
2.Цель работы.
3.Приборы и принадлежности.
4.Расчетные формулы:
61

|
момент инерции маятника Обербека: |
I= |
|
|
|
|
|
||
|
|
|
|
∆I= |
|
|
|
|
|
5. Измерения: |
|
|
|
|
|
|
|
|
|
|
радиус шкива: |
R= |
∆R= |
|
|
R |
= |
||
|
|
|
|
||||||
|
|
|
|
|
|
R |
|||
|
масса груза: |
m= |
∆т= |
|
|
m |
|
||
|
|
|
|
||||||
|
|
|
|
|
|
m |
|||
|
высота: |
h= |
∆h= |
|
|
h |
= |
||
|
|
|
|||||||
6. Таблица результатов наблюдений и вычислений: |
|
h |
|||||||
|
|
|
|
|
|||||
|
№ <l>, м |
t1 ,c |
t2 ,c |
t3 ,c |
<t>,c |
I, кг∙м2 |
|||
1
2
3
4
5
7.График I=ƒ(l).
8.Расчет момента инерции маятника Обербека:
<I1>= ∆I1=
I1 ∙100%=
I1
Окончательный результат: I1= 9. Выводы.
62
ЛАБОРАТОРНАЯ РАБОТА № М10
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛА МЕТОДОМ СРАВНЕНИЯ С ПОМОЩЬЮ МАШИНЫ АТВУДА
Цель работы: изучить вращательное движение твёрдого тела; определить момент инерции тела методом сравнения.
Приборы и принадлежности: установка, цилиндрическое тело, тело неопределённой формы, штангенциркуль.
I. ОПИСАНИЕ УСТАНОВКИ И МЕТОДА ИЗМЕРЕНИЙ
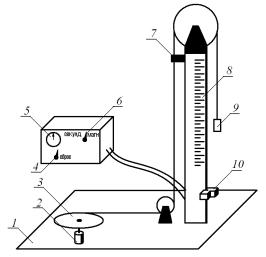
На массивном основании 1 (рис.1) установлена обойма 2 с шарикоподшипником, на вертикальной оси которого закреплён столик 3 в виде диска. Столик способен вращаться с незначительным трением. На круговой желоб диска наматывается капроновая нить, к противоположному концу которой прикреплён груз 9. Нить с помощью блоков из горизонтальной плоскости переходит в вертикальную. Один из блоков установлен сверху вертикальной штанги 8. Шкала штанги имеет сантиметровые деления от 0 до 86 см.
Рис. 1. Схема установки: 1 – основание; 2 – обойма; 3 – столик; 4 – рычаг сброса; 5 – секундомер; 6 – тумблер; 7 – электромагнит;
8– вертикальная штанга; 9 – груз; 10 – приёмный столик.
Вверхней части штанги установлен электромагнитный пускатель 7. Нить пропускается между якорем и сердечником
63
электромагнита. На обратной стороне штанги имеется специальный паз с двумя токоведущими шинами, через которые выключается цепь управления секундомером 5 с помощью приёмного столика 10. Устанавливая приёмный столик 10 в различных положениях штанги, можно изменять высоту падения груза 9. Груз фиксируется на нулевом делении штанги с помощью электромагнита 7. При переводе тумблера 6 в положение «магнит» якорь притягивается к сердечнику, зажимает нить, и груз надёжно фиксируется в нужном положении.
Если тумблер 6 перевести в положение «секундомер», то электромагнит освобождает нить и груз начинает падать. В этот момент секундомер включается и фиксирует время движения груза до соприкосновения его с приёмным столиком 10. При падении груза на приёмный столик цепь питания секундомера размыкается, и прекращается отсчёт времени.
Груз 9, удерживаемый на высоте h над приёмным столиком 10, обладает потенциальной энергией: Eп mгр gh.
Если предоставить грузу возможность падать, то его падение будет происходить с ускорением a . Под действием падающего груза столик-диск с расположенными на нём телами будет вращаться с угловым ускорением ε.
Если пренебречь наличием сил трения в осях вращающихся частей установки и силами сопротивления среды, то при падении груза его потенциальная энергия соответственно переходит в кинетическую энергию поступательного движения груза:
Eпост |
m |
гр |
V 2 |
|
|
|
||||
|
|
|
|
и |
кинетическую энергию вращательного движения |
|||||
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|||
столика: |
E |
|
|
I |
2 |
. |
||||
вр |
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
||
На основе закона сохранения механической энергии запишем уравнение:
mгр gh |
mгрV 2 |
|
I |
2 |
, |
(1) |
|
|
|
||||
2 |
2 |
|
|
|
||
где mгр - масса груза; V – скорость груза в момент падения; -
угловая скорость вращающегося столика; I – момент инерции столика относительно оси вращения.
Угловую скорость вращения столика можно выразить через линейную скорость точек поверхности кругового желоба столика:
64
|
V |
, |
(2) |
|||
R |
||||||
|
|
|
|
|||
где R – радиус столика. |
|
|
||||
Груз движется поступательно вертикально вниз без начальной |
||||||
скорости с постоянным ускорением: |
|
|
||||
a |
2h |
|
, |
(3) |
||
t2 |
||||||
|
|
|
||||
где t – время, за которое груз проходит расстояние h.
Если нить, на которую подвешен груз, нерастяжима и сматывается со столика без проскальзывания, то касательное ускорение точек поверхности желоба будет равно ускорению
опускающегося груза: a |
a. |
|
|
|
|
|
|
|||
Так как скорость груза в момент падения: V = at, то линейная |
||||||||||
скорость точек поверхности желоба в этот же момент: |
|
|||||||||
|
|
|
V a t |
2h |
. |
(4) |
||||
|
|
|
||||||||
|
|
|
|
|
|
|
t |
|
||
Используя выражения (2) и (4), соотношение (1) можно |
||||||||||
преобразовать и записать в следующем виде: |
|
|||||||||
m |
|
g |
2h |
m |
|
R2 I . |
(5) |
|||
гр |
R2t2 |
гр |
||||||||
|
|
|
|
|
|
|
||||
Из соотношения (5) видно: если во время эксперимента не изменять mгр , h, R, то с изменением момента инерции вращающегося
столика относительно неизменной оси вращения будет изменяться время опускания груза.
Запишем соотношение (5) для случаев:
1)Столик не нагружен. Тогда I Iст - момент инерции столика. Выражение (5) примет вид:
|
mгр g |
2h |
|
|
mгр R2 |
Iст . |
|
(6) |
|
R2t1 |
2 |
|
|||||
|
|
|
|
|
Iц , где Iц |
|||
2) |
На столике расположен цилиндр. В этом случае I Iст |
|||||||
|
- момент инерции цилиндра. |
|
|
|
|
|
|
|
|
mгр g |
2h |
|
|
mгр R2 |
Iст Iц . |
|
(7) |
|
R2t2 |
2 |
|
|
||||
|
|
|
|
|
|
|
||
3) |
На столике расположено испытуемое тело. Теперь I Iст |
Iх , где |
||||||
|
Iх - момент инерции испытуемого тела. |
|
|
|||||
|
|
|
65 |
|
|
|
||
|
mгр g |
|
2h |
|
|
mгр R2 |
|
Iст |
Ix . |
(8) |
||||||||||||
|
R2t3 |
2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Iст I0 , тогда |
|
||||||||
Введем |
обозначение |
|
|
|
mгр R2 |
предыдущие |
||||||||||||||||
соотношения (6), (7), (8) примут вид: |
|
|
|
|
|
|
|
|||||||||||||||
|
m |
|
g |
2h |
|
|
I |
|
; |
|
|
|
|
|
(9) |
|||||||
|
гр |
R2t1 |
2 |
0 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
mгр g |
|
|
2h |
|
|
I |
0 |
|
Iц ; |
|
(10) |
||||||||||
|
|
R2t2 |
2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
m |
|
g |
|
2h |
|
|
I |
|
|
I |
|
. |
|
(11) |
|||||||
|
гр |
R2t3 |
2 |
|
0 |
|
x |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решая |
систему уравнений |
(9), |
(10) и |
(11) относительно Iх |
||||||||||||||||||
получаем: |
I |
|
I |
|
|
|
(t |
2 t |
|
2 ) |
. |
|
|
|
(12) |
|||||||
|
|
|
|
|
3 |
|
|
|
1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
x |
|
|
|
ц (t22 t12 ) |
|
|
|
|
|
|||||||||||
Момент инерции сплошного однородного цилиндра |
||||||||||||||||||||||
относительно оси цилиндра равен: |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Iц |
|
mr2 |
|
md |
2 |
|
, |
|
|
|
(13) |
||||||||||
|
|
2 |
8 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
где d – диаметр цилиндра, m – его масса.
Расчётная формула момента инерции испытуемого тела
принимает окончательный вид: |
|
|
|
|||
I |
|
|
md2 (t2 |
t2 ) |
|
|
x |
3 |
1 |
. |
(14) |
||
|
|
|||||
|
|
8(t22 t12 ) |
|
|||
II.ПОРЯДОК РАБОТЫ
1.Измерить диаметр d цилиндрического тела. Определить абсолютную погрешность измерения диаметра ∆d по прибору.
2.Записать массу цилиндрического тела т (она указана на установке). Определить абсолютную погрешность массы ∆т как погрешность постоянной величины.
3.Установить приёмный столик на расстоянии h от нулевого деления шкалы. Оценить абсолютную погрешность измерения высоты ∆h по прибору.
4.Груз 9 установить у нулевого деления шкалы и зафиксировать это положение путем переключения тумблера 6 в положение
66

«магнит». Посредством рычага 4 установить стрелку секундомера на нулевое деление.
5.Измерить время t1 падения груза с данной высоты h для случая ненагруженного столика 3. Для этого нажать кнопку под приемным столиком 11 и перевести тумблер 6 в положение «секундомер». При достижении грузом 9 столика 10 секундомер
выключается. Записать его показания. Опыт повторить 6 раз. Вычислить среднее значение времени опускания груза:
N
ti
t1 |
|
i 1 |
. Рассчитать абсолютную погрешность времени t1 по |
|
N |
||||
|
|
|
секундомеру.
6.Поставить на шпильку столика цилиндр и измерить время падения груза t2, руководствуясь пунктом 5. Опыт повторить 6 раз. Найти среднее значение времени <t2> и абсолютную погрешность измерения времени t2 по секундомеру.
7.Заменить цилиндр испытуемым телом и измерить время падения груза t3, руководствуясь пунктом 5. Опыт повторить 6 раз. Найти среднее значение времени <t3> и абсолютную погрешность измерения времени t3 по секундомеру.
8.Определить момент инерции испытуемого тела по формуле (14). Рассчитать его абсолютную погрешность по упрощенной формуле:
|
|
m 2 |
2 d 2 |
|
2 t1 |
|
2 |
|
|
2 t2 |
2 |
|
|
2 t3 2 |
||||||||
Iх |
Iх |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|||||
|
|
m |
d |
|
|
|
t1 |
|
|
|
2 |
|
|
t3 |
||||||||
и |
относительную |
погрешность: |
|
Ix |
|
∙100%. |
|
Записать |
||||||||||||||
|
Ix |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
окончательный результат: |
Ix ( Ix Ix ) |
|
кг∙м2. |
|
|
|
|
|
||||||||||||||
III.ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.Какое движение называется вращательным движением?
2.Записать основное уравнение динамики вращательного движения. Пояснить входящие в него величины.
3.Дать определение момента силы относительно оси. Записать формулу, единицу измерения. Пояснить входящие в формулу величины.
67

4.Дать определение момента силы относительно точки. Записать формулу, единицу измерения. Пояснить входящие в формулу величины. Изобразить на рисунке вектор момента силы.
5.Что называется моментом инерции тела относительно оси? В каких единицах измеряется момент инерции?
6.Как определяется момент инерции тела относительно оси, не проходящей через центр масс?
7.Записать формулу кинетической энергии вращательного движения. Пояснить входящие в неё величины.
8.Дать определение угловой скорости тела. Записать формулу, единицу измерения. Изобразить на рисунке вектор угловой скорости.
9.Дать определение углового ускорения. Записать формулу, единицу измерения. Изобразить на рисунке вектор углового ускорения.
10.Какова связь между угловой скоростью тела и скоростями точек этого тела?
IV. СОДЕРЖАНИЕ ОТЧЁТА
1.Титульный лист.
2.Цель работы.
3.Приборы и принадлежности.
4.Расчётные формулы:
|
момент инерции испытуемого тела: |
Ix |
|
|
5. |
Исходные данные: |
|
Ix |
|
|
|
|
||
|
масса цилиндра: т= |
∆т= |
|
|
6. |
Измерения: |
|
|
|
|
диаметр цилиндра: d= |
∆d= |
|
|
|
время опускания груза: |
|
|
|
|
столик ненагружен |
|
|
|
m = m
d = d
№ |
|
1 |
2 |
|
3 |
4 |
5 |
|
|
6 |
|
t1,с |
|
|
|
|
|
|
|
|
|
|
|
<t1>= |
|
|
∆t1= |
|
|
t1 |
|
|
|||
|
|
|
|
t1 |
|
||||||
|
|
|
|
|
|
|
|
|
|||
68
столик с цилиндрическим телом:
|
|
|
№ |
|
1 |
2 |
3 |
|
4 |
|
|
5 |
6 |
||
|
|
|
t2,с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
<t2>= |
|
∆t2= |
|
t2 |
|
|
|
|||||
|
|
|
|
|
t2 |
|
|
||||||||
|
столик с испытуемым телом: |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
№ |
|
1 |
2 |
3 |
|
4 |
|
|
5 |
6 |
||
|
|
|
t3,с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
<t3>= |
|
∆t3= |
|
t3 |
|
|
|
|||||
|
|
|
|
|
t3 |
|
|
||||||||
7. Расчет момента инерции испытуемого тела: |
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||
|
Ix |
|
|
|
|
|
|
|
|
|
|
|
|||
|
Ix |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Ix |
∙100%= |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Ix |
|
|
|
|
|
|
|
|
|
|
|
||
|
Окончательный результат: Ix |
|
|
|
|
|
|
|
|||||||
8. Выводы. |
|
|
|
|
|
|
|
|
|
|
|||||
69

ЛАБОРАТОРНАЯ РАБОТА № М11
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛА МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ
Цель работы: изучить вращательное движение тела; экспериментально определить момент инерции тела неопределенной формы методом крутильных колебаний.
Приборы и принадлежности: крутильный маятник, тело неопределенной формы, секундомер, штангенциркуль.
I. ОПИСАНИЕ УСТАНОВКИ И МЕТОДА ИЗМЕРЕНИЙ
Крутильный маятник состоит (рис.1) из стального диска 2, подвешенного на вертикальной упругой металлической проволоке 1. Нижний конец проволоки проходит через центр масс диска, а верхний конец закреплен в точке подвеса кронштейна. Под диском на продолжении его оси вращения имеется винт для крепления тела неопределенной формы 3, момент инерции которого требуется определить.
Рис.1. Схема установки: 1 - металлическая проволока; 2 – стальной диск; 3 – исследуемое тело неопределенной формы.
Если крутильный маятник повернуть на небольшой угол вокруг вертикальной оси и отпустить, то маятник под действием возникающих в проволоке упругих сил будет совершать гармонические крутильные колебания.
При гармонических крутильных колебаниях маятника потенциальная энергия упругой деформации закрученной проволоки переходит в кинетическую энергию вращательного движения маятника относительно вертикальной оси. Затем кинетическая энергия
70
