
Учебное пособие, модуль 2
.pdfФедеральное агентство по образованию Тольяттинский государственный университет Кафедра «Начертательная геометрия и черчение»
УЧЕБНОЕ ПОСОБИЕ
по курсу «Начертательная геометрия»
МОДУЛЬ №2
Тольятти 2007
УДК 514.18(076) ББК 22.15.3
Н36
Рецензент:
к.т.н., доцент А.Г. Егоров (ТГУ).
Н36 Начертательная геометрия. Модуль №2 : учеб.-метод. Пособие / сост. Т.А. Варенцова, Г.Н. Уполовникова. – Тольятти : ТГУ, 2007.- 48 с.
Содержит полный теоретический материал для успешного освоения студентами курса «Начертательная геометрия». Учебный материал разбит на 4 модуля. Каждый модуль является логически завершенной частью, заканчивается контрольными вопросами и тестом с ответами для самоконтроля студента.
Для студентов технических специальностей высших учебных заведений
Рекомендовано к изданию методической комиссией автомеханического института Тольяттинского государственного университета
© Т.А. Варенцова, Г.Н. Уполовникова, Составление, 2007 © Тольяттинский государственный Университет, 2007
2
3
Содержание |
|
Комплексный чертёж плоскости и поверхности.......................................................................... |
6 |
Задание плоскости на комплексном чертеже............................................................................... |
6 |
Взаимная принадлежность точки, прямой и плоскости.......................................................... |
7 |
Плоскости частного положения............................................................................................... |
9 |
Проецирующие плоскости................................................................................................. |
10 |
Горизонтально проецирующая плоскость.................................................................... |
10 |
Фронтально проецирующая плоскость......................................................................... |
10 |
Плоскости уровня (дважды проецирующие)..................................................................... |
11 |
Горизонтальная плоскость уровня................................................................................ |
11 |
Фронтальная плоскость уровня..................................................................................... |
12 |
Особые линии плоскости............................................................................................................ |
13 |
Горизонталь плоскости........................................................................................................... |
13 |
Фронталь плоскости................................................................................................................ |
14 |
Линия наибольшего наклона плоскости................................................................................ |
16 |
Прямая, параллельная плоскости................................................................................................ |
20 |
Взаимная параллельность плоскостей........................................................................................ |
21 |
Справочный материал................................................................................................................. |
22 |
Примеры изображения плоскостей общего и частного положения, заданные |
|
геометрическими фигурами ................................................................................................... |
22 |
Плоскости общего положения........................................................................................... |
22 |
Горизонтально проецирующие плоскости........................................................................ |
23 |
Фронтально проецирующие плоскости............................................................................. |
23 |
Горизонтальные плоскости уровня.................................................................................... |
23 |
Фронтальные плоскости уровня........................................................................................ |
24 |
Контрольные вопросы................................................................................................................. |
24 |
Тест № 1.................................................................................................................................. |
25 |
Задание поверхности на комплексном чертеже......................................................................... |
25 |
Определитель поверхности .................................................................................................... |
26 |
Очерк проекции поверхности................................................................................................. |
26 |
Классификация поверхностей................................................................................................ |
27 |
Алгоритм конструирования поверхности.............................................................................. |
28 |
Задание линейчатых поверхностей на комплексном чертеже................................................... |
30 |
Развертывающиеся поверхности............................................................................................ |
30 |
Многогранные поверхности............................................................................................... |
30 |
Комплексный чертеж пирамидальной поверхности......................................................... |
31 |
Комплексный чертеж призматической поверхности........................................................ |
36 |
Проецирующая призма....................................................................................................... |
38 |
Задание кривых линейчатых поверхностей................................................................................ |
39 |
Задание конической поверхности общего вида на комплексном чертеже........................... |
40 |
Задание цилиндрической поверхности общего вида на комплексном чертеже................... |
42 |
Неразвертывающиеся линейчатые поверхности с двумя направляющими.............................. |
44 |
Цилиндроид............................................................................................................................. |
46 |
4
Коноид..................................................................................................................................... |
49 |
Гиперболический параболоид................................................................................................ |
51 |
Поверхности вращения ............................................................................................................... |
52 |
Комплексный чертеж поверхности вращения общего вида.................................................. |
53 |
Поверхности вращения второго порядка.................................................................................... |
57 |
Цилиндр вращения.................................................................................................................. |
57 |
Конус вращения...................................................................................................................... |
57 |
Сфера....................................................................................................................................... |
58 |
Поверхности вращения второго порядка.................................................................................... |
60 |
Эллипсоид вращения.............................................................................................................. |
60 |
Эллипсоид сжатый............................................................................................................. |
61 |
Эллипсоид вытянутый........................................................................................................ |
61 |
Параболоид вращения ............................................................................................................ |
61 |
Гиперболоид вращения........................................................................................................... |
62 |
Алгоритм построения главного меридиана однополостного гиперболоида, ..................65 |
|
Торповерхность вращения 4 порядка....................................................................................... |
68 |
Винтовые поверхности................................................................................................................ |
75 |
Прямой геликоид .................................................................................................................... |
76 |
Наклонный геликоид.............................................................................................................. |
76 |
Контрольные вопросы................................................................................................................. |
80 |
Ответы на тест - № 4................................................................................................................... |
80 |
Справочный материал................................................................................................................. |
81 |
Задание плоскости на комплексном чертеже......................................................................... |
81 |
Задание поверхности на комплексном чертеже..................................................................... |
81 |
5
Комплексный чертёж плоскости и поверхности
В данном модуле вы познакомитесь с различными видами поверхностей и их модификациями, способами задания их на комплексном чертеже, особенностями построения. Узнаете, что простейшая поверхность - это плоскость.
Задание плоскости на комплексном чертеже
«Поверхность есть то, что имеет только длину и ширину»
(Евклид «Начала», 4 век до н.э., книга 1, определение 5.)
Как вы думаете?
1.Не дана ли в "Началах" трактовка поверхности слишком упрощенно?
2.Какая фигура в современном понимании имеет "только длину и ширину"?
3.Безразмерна ли плоскость, или она имеет границы?
4.Можно ли задать плоскость пространственными линиями?
Плоскость является частным случаем поверхности - это двумерная геометрическая фигура, она имеет только длину и ширину, и не имеет толщины. Обозначается прописными буквами греческого алфавита. Плоскость - это множество точек, но определяется она тремя точками (напомним, что прямую линию определяют две точки).
Плоскость можно задать на чертеже:
1. Тремя точками: (А, В, С);
А2 В2 С2
А1 В1 С1
2. Прямой и точкой, не лежащей на данной прямой: Г(а, В);
а2 В2
а1
В1
Двумя параллельными прямыми: (с а);
а2
с2
с1
а1
3. Двумя пересекающимися прямыми: (m n);
6

т2 

 п2
п2
п1 
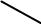 т1
т1
4. Любой плоской фигурой: (АВС);
|
|
|
|
В |
|||
|
|
|
|
2 |
|
|
|
А |
|
|
|
С |
|||
|
|
|
2 |
||||
|
|||||||
2 |
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
С |
|
|
|
|
||||
1 |
|
|
|
1 |
|||
|
|
|
|
|
|
|
|
В1
5. Своей главной проекцией: ( 1);
1
6. Линией наибольшего наклона плоскости (g1 ,g2);
g2
g1
Рис. 2-1
Плоскости бывают общего и частного положения
|
|
|
|
|
|
|
|
Плоскость |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общего положения |
|
|
|
|
|
Частного положения |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Проецирующие |
|
|
|
|
Плоскости уровня |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Горизонтально |
|
Фронтально |
|
Профильно |
|
Горизонтальная |
|
Фронтальная |
|
Профильная |
|||||||||
|
проецирующая |
|
проецирующая |
|
проецирующая |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Рис. 2-2
Если плоскость не перпендикулярна ни одной из плоскостей проекций,
то она называется плоскостью общего положения
Примеры чертежа плоскости общего положения см. варианты 1 - 5; 7 (рис. 2-1).
Взаимная принадлежность точки, прямой и плоскости
Точка принадлежит плоскости, если она принадлежит какой-нибудь прямой, лежащей в этой плоскости.
7

Построение точки в плоскости сводится к двум операциям: построению в плоскости вспомогательной прямой и построению точки на этой прямой.
Задача: Плоскость задана пересекающимися прямыми а и b (рис. 2-3). Точка М(М2 ) принадлежит плоскости.
Найти М1.
Краткая запись условия задачи: (а b), М(М2 ) ; М1 = ?
а2 b2
 M2
M2
 a1
a1
b1
Рис. 2-3
Решение: Через точку М2 (рис. 2-4) проводим вспомогательную прямую k : k2 a2 =12; k2 b2 =22;
затем находим горизонтальные проекции точек 1 и 2 по условию принадлежности прямым а и b соответственно; через две точки 11 и 21 проводим прямую k1 и на ней, с помощью линии связи, находим точку М1. И таких прямых можно провести сколько угодно, то есть, вариантов решения бесчисленное множество.
12а2 k2 22 b2M2
k1 |
|
21 |
|
M1 |
|
|
|||
|
|
|||
|
|
|
|
|
1 |
|
a1 |
||
1 |
|
|
|
|
b1 |
|
|
|
|
Рис. 2-4
Прямая принадлежит плоскости, если она:
1.Проходит через две точки плоскости;
2.Проходит через одну точку плоскости и параллельна какой-нибудь прямой, лежащей
вэтой плоскости.
В предыдущем примере мы рассмотрели, как построить прямую в плоскости по двум точкам. Для второго случая плоскость Г зададим треугольником АВС.
8
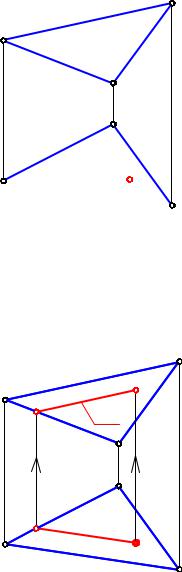
Задача: Плоскость Г задана АВС (рис. 2-5).
Точка М(М1) принадлежит Г. Найти М2.
М(М1) Г(АВС). М2 = ?
А2 В2
С2
С1
М1 А1  В1
В1
Рис. 2-5
Решение:
Через точку М1 (рис.2-6) проведём прямую k, параллельную стороне треугольника АВ. Она пересечёт сторону АС в точке 1: k1 A1 B1 ; k1 A1 C1 =11; с помощью линии связи найдём 12, проведём k2 параллельно А2В2 ней найдём точку М2:
В2
А |
|
М |
|
2 |
|
2 |
|
k2 |
12 |
|
|
|
С |
|
|
|
|
|
|
2 |
|
|
С |
|
|
1 |
11 |
k |
М |
|
1 |
1 |
А1
В1
Рис. 2-6
Алгоритмическая запись решения:
11 A1C1 12 A2C2; 12 k2, k2 A2B2; M2 k2.
Как вы думаете?
Сколько решений имеет эта задача?
Плоскости частного положения
Плоскости, параллельные или перпендикулярные одной из плоскостей проекций,
называются плоскостями частного положения.
Имеется две группы таких плоскостей:
1.Проецирующие плоскости
2.Плоскости уровня
9
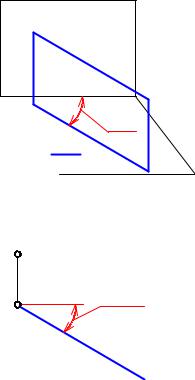
Проецирующие плоскости
Если плоскость перпендикулярна только одной плоскости проекций, то она называется
проецирующей.
Одна из её проекций вырождается в прямую линию, называемую главной проекцией и обладающую собирательными свойствами.
Горизонтально проецирующая плоскость
Это плоскость, перпендикулярная горизонтальной плоскости проекций: Г П1
(рис. 2-7а, 2-7б).
Графический признак:
Горизонтальная проекция Г1 горизонтально проецирующей плоскости прямая линия, не параллельная и не перпендикулярная линиям связи. Это главная проекция.
Например:
Г П1 - горизонтально проецирующая плоскость.
Г П1 Г1 - прямая линия, главная проекция.
- угол наклона плоскости Г к П2.
Г
 Г1
Г1 
П2
П1
Рис. 2-7а
Пространственный чертеж
Г1
Рис. 2-7б
Плоский чертеж
Фронтально проецирующаяплоскость
Это плоскость, перпендикулярная фронтальной плоскости проекций: П2
(рис. 2-8а, 2-8,б)
Графический признак:
Фронтальная проекция 2 фронтально проецирующей плоскости - прямая линия, не параллельная и не перпендикулярная линиям связи. Это главная проекция.
10
