На рис.13 решена задача построения проекций поверхности кольца с фронтально – проецирующей осью i. Этот пример отличается от предыдущего тем, что все окружности, описываемые точками образующей, проецируются в истинном виде на поле П2, а на поле П1 в отрезки. На рис.13a изображены две проекции такой окружности – параллели f для некоторой т.M образующей. На рис. 13б изображены проекции поверхности с обозначениями:n – горло.m –

экватор.k, k – окружности линии контура для горизонтальной проекции кольца.

При построении точек на поверхности кольца нужно твёрдо помнить, что кольцо – поверхность нелинейчатая, и существует только одно семейство окружностей на этой поверхности, которые легко строить на комплексном чертеже. Это окружности – параллели, плоскости которых перпендикулярны оси вращения.

Здесь же построены проекции двух точек на поверхности: A(A1), A2 = ? и B(B1), B2 = ? Проекции окружности параллели f(f1,f2), которая проведена через т. A построены полностью.

Для построения горизонтальной проекции т. B проведена окружность f ( f 1 , f 2 ), проекции

которой построены не полностью. Следует обратить внимание на область видимых точек поверхности относительно плоскости П1 (отмечена штриховкой). Такая видимость поверхности относительно плоскости П1 объясняется особенностью формы поверхности кольца.

4.4 Построение проекций винтовых поверхностей

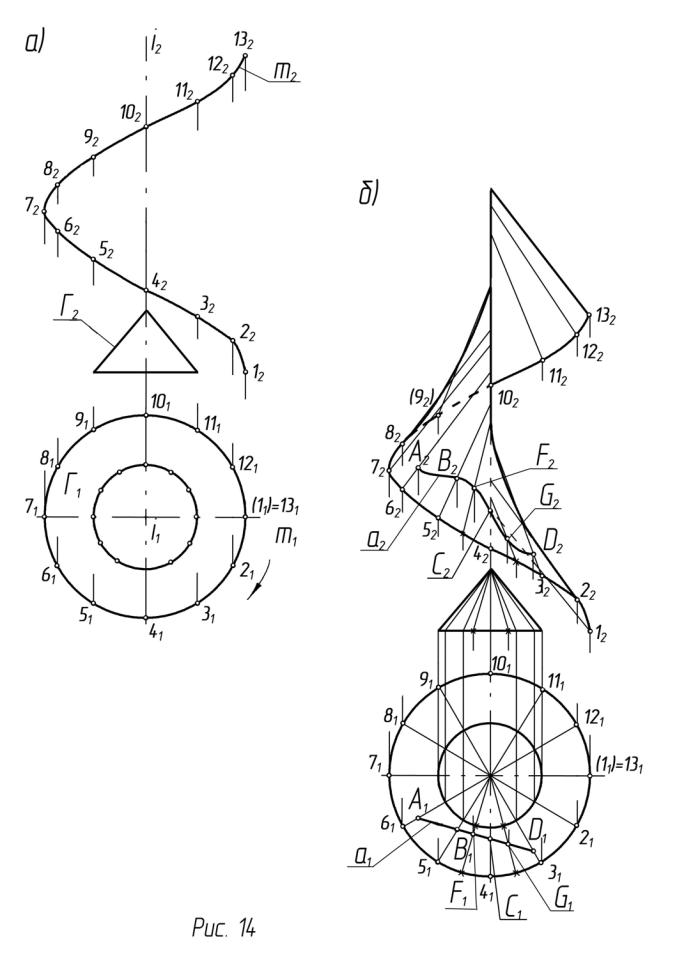
Мы изучаем винтовые линейчатые поверхности, которые называются геликоидами. В заданиях эпюра предусмотрены как наклонные, так и прямые закрытые геликоиды. При построении проекций поверхностей следует помнить, что они являются линейчатыми и на комплексном чертеже задаются каркасом образующих. На рис. 14а дано условие задачи – проекции определителя наклонного закрытого геликоида Ф(m,Г), где m – винтовая направляющая, Г- направляющий конус. Для построения проекций направляющей винтовой линии m надо брать не менее двенадцати точек, обводку выполнять по лекалу. На рис. 14б в результате построения дискретного каркаса из двенадцати образующих получены проекции поверхности. В каждом положении образующая геликоида lгел. параллельна соответствующей образующей направляющего конуса lк . Алгоритмическую

24

Часть определителя (закон каркаса) можно записать так: li гел ∩m, li гел //liк.

Проекции промежуточных образующих следует выполнять тонкими линиями. Все линии, ограничивающие проекции поверхности подлежат обводке, в том числе линии обреза – крайние образующие. Обязательно строится линия контура (очерковая) относительно плоскости П2 как огибающая семейства прямолинейных образующих.

На рис. 14б показано построение линии a, принадлежащей поверхности геликоида. Задана горизонтальная проекция a1 в видеотрезка, a2 надо построить. Линия, принадлежащая геликоиду, может быть прямой только тогда, когда она является его образующей.В нашем примере линия a не является образующей. Следовательно, линия a – плоская кривая, т.к. вырождаться в прямую может только проекция плоской кривой. Для построения проекции кривой линии выделяем несколько точек. Следовательно, построение проекций линии на поверхности сводится к построению проекций точек на поверхности. Проекции точек A,B,C и D строятся по принадлежности соответствующим образующим. Фронтальную проекцию т. С в системе 2-х плоскостей проекций построить сложнее. Поэтому между соответствующими образующими каркас уплотняем – вводим ещё две образующие, т.е. строим последовательно их горизонтальные, а потом фронтальные проекции. Отмечаем точки F1 иG1 и построением F2 и G2 заканчиваем решение задачи.

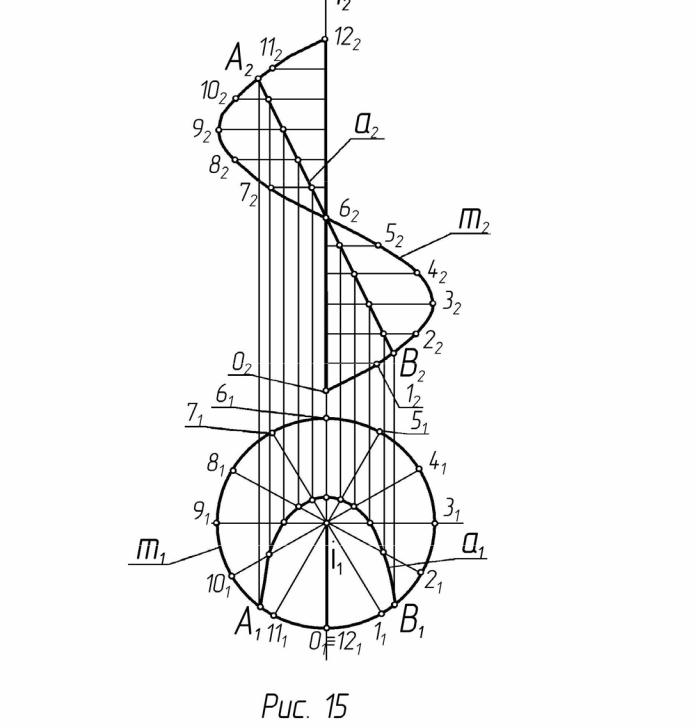
В качестве последнего примера рассмотрим построение проекций прямого геликоида. Все образующие прямого геликоида перпендикулярны оси направляющей винтовой линии, т.е. направляющий конус вырождается в плоскость параллелизма. Для прямого геликоида Ф (i, m, П1) элементы геометрического определителя: i и m направляющие, П1 – плоскость параллелизма, т.к. ось винтовой линии обычно располагают перпендикулярно плоскости П1. Алгоритмический определитель (закон каркаса): li ∩ i, li ∩ m, li // П1,,т.е. все образующие являются горизонтальными прямыми. На рис. 15 показаны проекции поверхности прямого закрытого геликоида, заданного каркасом из двенадцати образующих. Задана фронтальная проекция линии a, принадлежащей поверхности. Выделены точки, принадлежащие образующим, и построены их горизонтальные проекции, в результате чего определена горизонтальная проекция линии а, кривая а1. Между образующими 6 и 5, 7 и 6 проведены дополнительные образующие, т.е. каркас уплотнён. Из чертежа видно, что все построения, связанные с построением проекций прямого геликоида, намного проще, чем в предыдущем примере.

26